根据以上数据，构建一个组距为5的频数分布表，第一个区间为0-5（不包含5）。从这个表格表示中，你观察到了哪些主要特征？

40名工程师从住所到工作地点的距离（单位：公里）

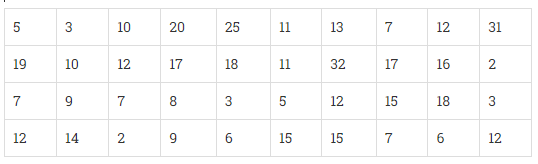
根据以上数据，构建一个组距为5的频数分布表，第一个区间为0-5（不包含5）。从这个表格表示中，你观察到了哪些主要特征？

 已知

40名工程师从住所到工作地点的距离（单位：公里）

任务

我们必须根据以上数据，构建一个组距为5的频数分布表，第一个区间为0-5（不包含5）。

解答

给定数据量较大，为方便起见，我们构建一个组距为5的频数分布表。

这意味着：

区间为0-5, 5-10, 10-15, 15-20等等。

数据在分组频数分布表中的表示如下：

距离（公里）计数频数
0-5
5
5-10
11
10-15
11
15-20
9
20-25|1
25-30|1
30-35||2
总计
40

从上表可以看出，各组之间没有重叠。

此外，40名工程师中有36名工程师的住所距离工作地点不到20公里。

更新于：2022年10月10日

浏览量：30

开启你的职业生涯

完成课程获得认证

开始学习
广告