负载下的实际变压器

当负载阻抗连接到实际变压器的次级绕组时，则称变压器处于负载状态，并汲取流经次级绕组和负载的负载电流。

我们将考虑以下两种情况来分析实际变压器：

情况 1 - 当假设变压器没有绕组电阻和漏磁通时

该图显示了一个实际变压器，假设忽略了绕组电阻和漏抗。根据此假设，

$$\mathrm{𝑉_{1} = 𝐸_{1}\: 和 \:V_{2} = 𝐸_{2}}$$

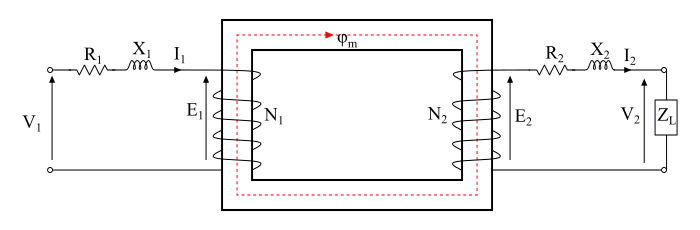
考虑一个感性负载连接到次级绕组，导致次级电流 I₂ 落后于次级电压 V₂ 一个角度 ϕ₂。在这种情况下，总初级电流 I₁ 必须满足两个要求：

• 首先，它必须提供空载电流 I₀ 以产生铁损和变压器铁芯中的磁通量。
• 其次，它必须提供电流 I’₂ 以抵消次级电流 I₂ 的退磁作用。

电流 I’₂ 的大小由下式给出：

$$\mathrm{𝑁_{1}I'_{2}= 𝑁_{2}I_{2}}$$

$$\mathrm{⇒ I'_{2}=\frac{𝑁_{2}}{𝑁_{1}}I_{2} = 𝐾I_{2}}$$

因此，负载条件下实际变压器汲取的总初级电流由 I’₂ 和 I₀ 的相量和给出，即

$$\mathrm{𝑰_{𝟏} = 𝑰'_{𝟐}+ 𝑰_{𝟎}}$$

其中，

$$\mathrm{𝐼’_{2} = − 𝐾I_{2}}$$

负号表示电流 I’₂ 与电流 I₂ 相差 180°。

相量图显示，两个电动势 E₁ 和 E₂ 都落后于互磁通 (ϕ_m) 90°。电流 I’₂ 表示初级电流的一部分，该部分抵消了次级电流 (I₂) 的退磁作用。因此，电流 I_’2 必须与 I₂ 反相。相量 I₀ 表示变压器的空载电流。I’₂ 和 I₀ 的相量和表示总初级电流 (I₁)。因此，

$$\mathrm{初级功率因数 = cos \varphi_{1}}$$

$$\mathrm{次级功率因数 = cos \varphi_{2}}$$

因此，

$$\mathrm{输入功率，𝑃_{1} = 𝑉_{1}𝐼_{1} cos \varphi_{1}}$$

$$\mathrm{输出功率，𝑃_{2} = V_{2}I_{2} cos \varphi_{2}}$$

情况 2 - 当变压器具有绕组电阻和漏磁通时

该图显示了一个具有绕组电阻和漏抗的实际变压器。这是实际变压器中存在的实际情况。这里，部分施加电压会降落在初级绕组电阻 R₁ 和漏抗 X₁ 上，因此初级电动势 (E ₁) 将小于施加电压 V₁。

类似地，在次级绕组电阻 R₂ 和漏抗 X₂ 上存在电压降，因此次级绕组端子上的电压 V₂ 将小于次级电动势 (E₂)。

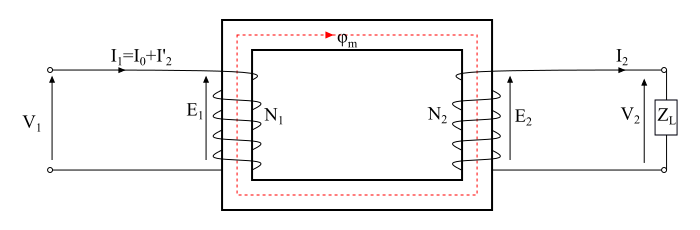
现在，考虑一个感性负载连接到变压器的次级绕组，导致次级电流 I₂ 落后于次级电压 V₂ 一个角度 ϕ₂，并且总初级电流 (I₁) 必须满足两个要求：

• 首先，它必须提供空载电流 I₀ 以产生铁损和变压器铁芯中的磁通量。
• 其次，它必须提供电流 I’₂ 以抵消次级电流 I₂ 的退磁作用。

电流 I'₂ 的大小由下式给出：

$$\mathrm{𝑁_{1}I'_{2}= 𝑁_{2}I_{2}}$$

$$\mathrm{⇒ I'_{2} =\frac{𝑁_{2}}{𝑁_{1}}I_{2} = 𝐾I_{2}}$$

因此，负载条件下实际变压器汲取的总初级电流由 I’2 和 I₀ 的相量和给出，即

$$\mathrm{𝑰_{𝟏} = 𝑰'_{𝟐} + Ｉ_{𝟎}}$$

其中，

$$\mathrm{𝐼’_{2} = − 𝐾I_{2}}$$

负号表示电流 I’₂ 与电流 I₂ 相差 180°。

现在，通过在初级回路和次级回路中应用 KVL，我们可以得到施加的初级电压 (V₁) 和次级端电压 (V₂) 为：

$$\mathrm{𝑽_{𝟏} = −𝑬_{𝟏} + 𝑰_{𝟏}(𝑹_{𝟏} + 𝒋𝑿_{𝟏})}$$

$$\mathrm{⇒ 𝑽_{𝟏} = −𝑬_{𝟏} + 𝑰_𝟏𝒁_𝟏}$$

和，

$$\mathrm{𝑽_{𝟐} = 𝑬_{𝟐} − 𝑰_{𝟐}(𝑹_{𝟐} + 𝒋𝑿_{𝟐})}$$

$$\mathrm{⇒ 𝑽_{𝟐} = 𝑬_{𝟐} − 𝑰_𝟐𝒁_𝟐}$$

粗体字母表示相量和。

从相量图可以看出，两个电动势 E₁ 和 E₂ 都落后于互磁通 (ϕ_m) 90°。电流 I’₂ 表示初级电流，以抵消次级电流 (I₂) 的退磁作用，该电流与 I₂ 反相。电流 I₀ 是变压器的空载电流。因此，总初级电流 (I₁) 由 I’₂ 和 I₀ 的相量和获得。

此外，初级电压 (V₁) 通过将 I₁R₁ 和 I₁X₁ 的降落（相量和）加到反电动势 (– E₁) 上而获得。次级端电压 V₂ 通过从电动势 (E₂) 中减去 (相量差) I₂R₂ 和 I₂X₂ 而获得。

输入和输出功率因数由下式给出：

$$\mathrm{输入功率因数 = cos\varphi_1}$$

$$\mathrm{输出功率因数 = cos\varphi_2}$$

此外，变压器的输入和输出功率由下式给出：

$$\mathrm{输入功率，𝑃1 = 𝑉_{1}𝐼_{1} cos \varphi_1}$$

$$\mathrm{输出功率，𝑃2 = V_{2}I_{2} cos \varphi_2}$$

数值示例

一个 440/120 V 单相变压器汲取 6 A 的空载电流，功率因数为 0.3 滞后。如果次级绕组以 0.85 滞后功率因数提供 100 A 的电流。确定初级绕组汲取的电流。

解决方案

这里，初级电流 I₁ 由 I’₂ 和 I₀ 的相量和给出，因此，

$$\mathrm{cos\varphi_0 = 0.3;\:\: \therefore\:\: \varphi_0 = 72.54°}$$

$$\mathrm{cos\varphi_2 = 0.85;\:\: \therefore \:\:\varphi_2 = 31.79°}$$

现在，变压比为：

$$\mathrm{𝐾 =\frac{V_{2}}{𝑉_{1}}=\frac{120}{440} =\frac{3}{11}}$$

因此，

$$\mathrm{I'_{2}= 𝐾I_{2} = (\frac{3}{11}) × 100 = 27.27 A}$$

参考相量图，I’₂ 和 I₀ 之间的角度为

$$\mathrm{\theta = 72.54 − 31.79 = 40.75°}$$

现在，使用平行四边形定则求矢量和，初级电流为

$$\mathrm{I_{1} = \sqrt{(I'_{2})^2 + (𝐼_{0})^2 + 2I_{0}I'_{2}cos \theta}}$$

$$\mathrm{⇒ 𝐼_{1} = \sqrt{(27.27)^2 + (6)^2 + (2 × 6 × 27.27 × cos 40.75)} = 32.05 A}$$

Manish Kumar Saini

更新于： 2021-08-21

7K+ 次查看

开启你的 职业生涯

通过完成课程获得认证

开始学习