数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究实用变压器空载运行
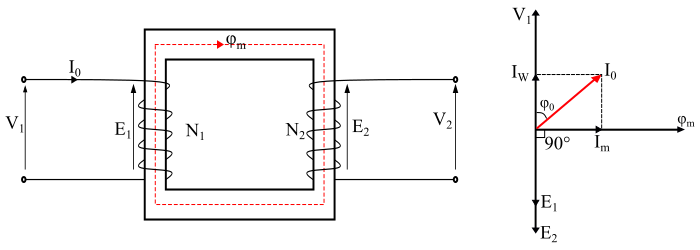
当实用变压器的次级绕组开路时，则称变压器处于空载状态（见图）。在这种情况下，初级绕组将从电源汲取一个小的空载电流 I0，该电流提供铁损和初级绕组中极少量的铜损。因此，初级空载电流 (I0) 与所加电压 V1 的相位差不是 90°，而是滞后于它一个 φ0 角，该角小于 90°。
因此，
$$\mathrm{空载输入功率，𝑃_{0} = 𝑉_{1}𝐼_{0} cos\varphi_{0}}$$
从相量图可以看出，空载初级电流 (I0) 可以分解成两个互相垂直的分量，即有功分量和磁化分量。
有功分量
分量 IW 与所加电压 V1 同相，称为有功分量或铁损分量。空载电流的这一分量负责提供铁损和变压器中极少量的初级绕组铜损。IW 由下式给出：
$$\mathrm{𝐼_{𝑊} = 𝐼_{0} cos\varphi_{0}}$$
磁化分量
分量 Im 滞后于所加电压 V1 90°，称为空载电流的磁化分量。磁化分量负责产生变压器铁芯中的互感磁通 φm，并由下式给出：
$$\mathrm{𝐼_{𝑚} = 𝐼_{0} sin \varphi_{0}}$$
因此，空载电流 I0 是 IW 和 Im 的相量和，即
$$\mathrm{𝐼_{0} = \sqrt{𝐼_{𝑊}^{2} + 𝐼_{𝑚}^{2}}}$$
此外，空载功率因数由下式给出：
$$\mathrm{cos \varphi_{0} =\frac{𝐼_{𝑊}}{𝐼_{0}}}$$
需要注意的是，在实用变压器中，空载时的初级绕组铜损非常小，可以忽略不计。因此，实用变压器的空载输入功率等于变压器铁芯中的铁损，即
$$\mathrm{空载输入功率， 𝑃_{0} = 铁损}$$
此外，在空载时，次级绕组中没有电流流动。因此，E2 = V2。
实用变压器的空载等效电路
当变压器处于空载状态时，次级绕组中没有电流流动。尽管初级绕组汲取了一个小的空载电流 (I0)，该电流提供磁化电流 (Im) 以在铁芯中产生磁通，以及电流 IW 以提供铁芯损耗。因此，空载初级电流被分成两个分量，因此可以用两个并联支路表示，这两个并联支路由一个与初级绕组并联的并联电路 R0 – Xm 组成。
电阻 R0 称为铁损电阻，表示铁损（即磁滞损耗和涡流损耗），因此电流 IW 流过 R0 支路。电感抗 Xm 称为磁化电抗，表示一个无损线圈，用于在铁芯中产生磁通，因此磁化电流 Im 流过它。
铁损电阻 (R0) 由下式给出：
$$\mathrm{𝑅_{0} =\frac{𝑉_{1}}{𝐼_{𝑊}}}$$
磁化电抗 (Xm) 由下式给出：
$$\mathrm{𝑋_{𝑚} =\frac{𝑉_{1}}{𝐼_{𝑚}}}$$
需要注意的是，在实用变压器中，电流 IW 与电流 Im 相比非常小。因此，实用变压器的空载功率因数 (cosφ0) 非常小。
数值例子
一个 240/2200 V 变压器汲取 5 A 的空载电流并吸收 200 W。如果初级绕组的电阻为 0.08 Ω。确定以下内容 -
铁损
空载功率因数
空载电流的有功分量
磁化电流
解决方案
变压器在空载时吸收的功率提供铁损和初级绕组铜损。因此，
$$\mathrm{初级绕组铜损 = 𝐼_{0}^{2}𝑅_{1} = 5^2 × 0.08 = 2\:W}$$
铁损
$$\mathrm{铁损 = 𝑃_{0} − 初级绕组铜损}$$
$$\mathrm{⇒ 铁损 = 200 − 2 = 198 \:W}$$
空载功率因数
$$\mathrm{cos \varphi_{0} =\frac{𝑃_{0}}{𝑉_{1}𝐼_{0}}=\frac{200}{240 × 5}= 0.167 (滞后)}$$
空载电流的有功分量
$$\mathrm{𝐼_{𝑊} = 𝐼_{0} cos\varphi_{0} = 5 × 0.167 = 0.835 A}$$
磁化电流
$$\mathrm{I_{m}=\sqrt{I_0^2-I_W^2}=\sqrt{(5)^{2}-(0.835)^{2}}=4.93\:A}$$
6K+ 次浏览
