数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学使用 C++ 打印给定二叉树节点的祖先节点（非递归）
在这个问题中，我们给定一棵二叉树，需要打印出二叉树中某个节点的祖先节点。
二叉树是一种特殊的树，其每个节点最多有两个子节点。因此，每个节点要么是叶子节点，要么有一个或两个子节点。
例如：
**祖先节点**是指在二叉树中位于给定节点上层的一个节点。
让我们来看一个祖先节点的例子：
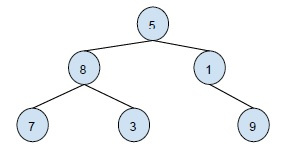
在这棵二叉树中，值为 3 的节点的祖先节点是 **8**，
为了解决这个问题，我们将从根节点遍历到目标节点，逐步向下遍历二叉树。并在路径中打印所有遇到的节点。
这理想情况下会涉及到对路径中从根节点到目标节点的每个节点都进行相同方法的递归调用。
因此，非递归方法需要使用迭代遍历和一个栈，该栈将存储树中目标节点的祖先节点。我们将进行二叉树的后序遍历。并将祖先节点存储到栈中，最后打印栈的内容，这些内容就是该节点的祖先节点。
示例
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 100
struct Node{
int data;
struct Node *left, *right;
};
struct Stack{
int size;
int top;
struct Node* *array;
};
struct Node* insertNode(int data){
struct Node* node = (struct Node*) malloc(sizeof(struct Node));
node->data = data;
node->left = node->right = NULL;
return node;
}
struct Stack* createStack(int size){
struct Stack* stack = (struct Stack*) malloc(sizeof(struct Stack));
stack->size = size;
stack->top = -1;
stack->array = (struct Node**) malloc(stack->size * sizeof(struct Node*));
return stack;
}
int isFull(struct Stack* stack){
return ((stack->top + 1) == stack->size);
}
int isEmpty(struct Stack* stack){
return stack->top == -1;
}
void push(struct Stack* stack, struct Node* node){
if (isFull(stack))
return;
stack->array[++stack->top] = node;
}
struct Node* pop(struct Stack* stack){
if (isEmpty(stack))
return NULL;
return stack->array[stack->top--];
}
struct Node* peek(struct Stack* stack){
if (isEmpty(stack))
return NULL;
return stack->array[stack->top];
}
void AncestorNodes(struct Node *root, int key){
if (root == NULL) return;
struct Stack* stack = createStack(MAX_SIZE);
while (1){
while (root && root->data != key){
push(stack, root);
root = root->left;
}
if (root && root->data == key)
break;
if (peek(stack)->right == NULL){
root = pop(stack);
while (!isEmpty(stack) && peek(stack)->right == root)
root = pop(stack);
}
root = isEmpty(stack)? NULL: peek(stack)->right;
}
while (!isEmpty(stack))
printf("%d ", pop(stack)->data);
}
int main(){
struct Node* root = insertNode(15);
root->left = insertNode(10);
root->right = insertNode(25);
root->left->left = insertNode(5);
root->left->right = insertNode(12);
root->right->left = insertNode(20);
root->right->right = insertNode(27);
root->left->left->left = insertNode(1);
root->left->right->right = insertNode(14);
root->right->right->left = insertNode(17);
printf("The ancestors of the given node are : ");
AncestorNodes(root, 17);
getchar();
return 0;
}输出
The ancestors of the given node are : 27 25 15
更新于：2020年1月3日
135 次查看
广告