数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学在C语言中打印完美二叉树的中间层，无需查找高度
程序应该打印二叉树的中间层，例如，如果二叉树有4层，那么程序必须打印第2层的节点，但这里要求是在不查找高度的情况下计算层数。
完美二叉树是指内部节点必须有两个子节点，并且所有叶子节点都应在同一层或深度。
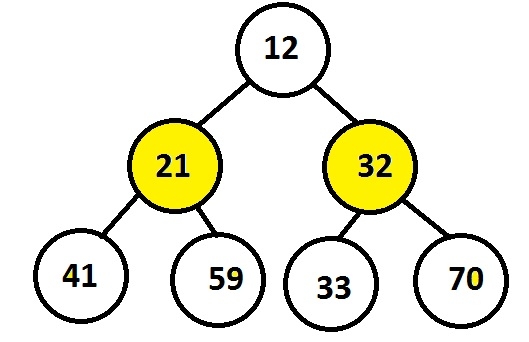
这里：
内部节点21和32都有子节点。
叶子节点是41、59、33和70，它们都在同一层。
因为它满足这两个属性，所以它是一个完美的二叉树。
示例
Input : 12 21 32 41 59 33 70 Output : 21 32
这里使用的方法就像查找链表的中间元素一样，通过检查节点的左指针和右指针是否为NULL来进行递归调用函数。
下面的代码显示了给定算法的C语言实现。
算法
START Step 1 -> create node variable of type structure Declare int key Declare pointer of type node using *left, *right Step 2 -> create function for inserting node with parameter as value Declare temp variable of node using malloc Set temp->data = value Set temp->left = temp->right = NULL return temp step 3 - > Declare Function void middle(struct Node* a, struct Node* b) IF a = NULL||b = NULL Return IF ((b->left == NULL) && (b->right == NULL)) Print a->key Return End Call middle(a->left, b->left->left) Call middle(a->right, b->left->left) Step 4 -> Declare Function void mid_level(struct Node* node) Call middle(node, node) Step 5 -> In main() Call New passing value user want to insert as struct Node* n1 = New(13); Call mid_level(n1) STOP
示例
#include <stdio.h>
#include<stdlib.h>
struct Node {
int key;
struct Node* left, *right;
};
struct Node* New(int value) {
struct Node* temp = (struct Node*)malloc(sizeof(struct Node));
temp->key = value;
temp->left = temp->right = NULL;
return (temp);
}
void middle(struct Node* a, struct Node* b) {
if (a == NULL || b == NULL)
return;
if ((b->left == NULL) && (b->right == NULL)) {
printf("%d ",a->key);
return;
}
middle(a->left, b->left->left);
middle(a->right, b->left->left);
}
void mid_level(struct Node* node) {
middle(node, node);
}
int main() {
printf("middle level nodes are : ");
struct Node* n1 = New(13);
struct Node* n2 = New(21);
struct Node* n3 = New(44);
struct Node* n4 = New(98);
struct Node* n5 = New(57);
struct Node* n6 = New(61);
struct Node* n7 = New(70);
n2->left = n4;
n2->right = n5;
n3->left = n6;
n3->right = n7;
n1->left = n2;
n1->right = n3;
mid_level(n1);
}输出
如果我们运行上面的程序，它将生成以下输出。
middle level nodes are : 21 44
更新于：2019年8月22日
162 次浏览
广告