数据结构
网络
关系型数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究C++程序：计算加权路径图中为真的查询数量
假设我们有一个无向图的边列表，其中每条边都有[u, v, w]字段，u和v是源和目标顶点，w是权重。并且还有一个相同格式[u, v, w]的查询列表。这表示一个问题：是否存在一条从u到v的路径，使得路径中的每条边的权重都最多为w。所以找到为真的查询数量。
因此，如果输入类似于 edges = [[0, 1, 6],[1, 2, 7],[2, 3, 8],[0, 3, 5]] queries = [[0, 2, 14],[1, 0, 3]]
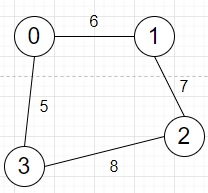
那么输出将是1，因为我们可以通过遵循这条路径[0, 1, 2]（权重为13）从节点0到达节点2。但是从1到0没有权重为3的路径。
为了解决这个问题，我们将遵循以下步骤：
- 定义一个函数get_parent()，它将接收x、数组par作为参数，
- 如果par[x]不等于x，则
- par[x] := get_parent(par[x], par)
- 返回par[x]
- 从主方法执行以下操作：
- 定义一个二维数组gr
- n := 0
- 对于edges中的每个边t：
- n := n、t[0]和t[1]中的最大值
- 将一行[t[2], 0, t[0], t[1]]插入到gr中
- 对于queries中的每个查询t：
- 将一行[t[2], 1, t[0], t[1]]插入到gr中
- 对gr进行排序
- 定义一个大小为n+1的数组par，并用-1填充
- 初始化i := 0，当i <= n时，更新（i加1），执行以下操作：
- par[i] := i
- sz := queries的大小
- ans := 0
- 对于gr中的每一行t：
- a := t[2]，b := t[3]，tp := t[1]，d := t[0]
- px := get_parent(a, par)
- py := get_parent(b, par)
- 如果tp等于0，则：
- 如果px不等于py，则：
- par[py] := px
- 如果px不等于py，则：
- 否则
- 如果px等于py，则：
- （ans加1）
- （sz减1）
- 如果sz等于0，则：
- 退出循环
- 如果px等于py，则：
- 返回ans
示例（C++）
让我们看看以下实现以获得更好的理解：
#include <bits/stdc++.h>
using namespace std;
int get_parent(int x, vector<int>& par) {
if (par[x] != x) {
par[x] = get_parent(par[x], par);
}
return par[x];
}
int solve(vector<vector<int>>& edges, vector<vector<int>>& queries) {
vector<vector<int>> gr;
int n = 0;
for (auto t : edges) {
n = max(n, max(t[0], t[1]));
gr.push_back({t[2], 0, t[0], t[1]});
}
for (auto t : queries) {
gr.push_back({t[2], 1, t[0], t[1]});
}
sort(gr.begin(), gr.end());
vector<int> par(n + 1, -1);
for (int i = 0; i <= n; i++) {
par[i] = i;
}
int sz = queries.size();
int ans = 0;
for (auto t : gr) {
int a = t[2];
int b = t[3];
int tp = t[1];
int d = t[0];
int px = get_parent(a, par);
int py = get_parent(b, par);
if (tp == 0) {
if (px != py) {
par[py] = px;
}
}else {
if (px == py) {
ans++;
}
sz--;
if(sz == 0) {
break;
}
}
}
return ans;
}
int main(){
vector<vector<int>> edges = {{0, 1, 6},{1, 2, 7},{2, 3, 8},{0, 3, 5}};
vector<vector<int>> queries = {{0, 2, 14},{1, 0, 3}};
cout << solve(edges, queries);
}输入
{{0, 1, 6},{1, 2, 7},{2, 3, 8},{0, 3, 5}}, {{0, 2, 14},{1, 0, 3}}输出
1
更新时间： 2020年12月12日
65 次浏览
广告