3D 形状的投影面积

假设有一个 N x N 网格，我们放置一些与 x、y 和 z 轴对齐的 1 x 1 x 1 立方体。此处每个值 v = grid[i][j] 显示放置在网格单元格 (i,j) 上方的一个 v 立方体塔。我们从上面、前面和侧面查看这些立方体的投影。在从顶部、正面和侧面查看立方体时，我们必须找出所有三个投影的总面积。

因此，如果输入类似 [[1,2],[3,4]]

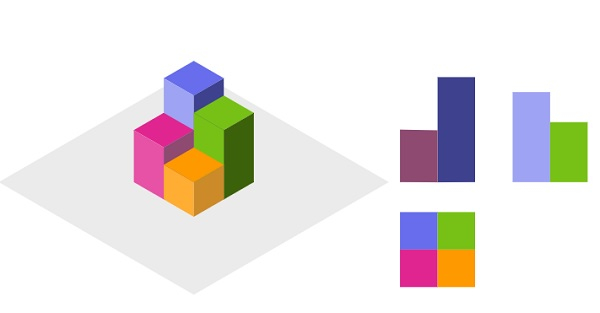
那么输出将是 17.

要解决此问题，我们将遵循以下步骤 −

  • xy := 0, yz := 0, xz := 0
  • 对每个行索引 r 和 grid 中的行 row 执行操作
    • yz := yz + 大于行的 row
    • 对于 row 中的每个列索引 c 和列 col 执行操作
      • 如果 grid[r][c] > 0 是非零，则
        • xy := xy + 1
    • 对于 grid 中的每个 col 执行操作
      • xz := xz + 最大 col
  • 返回 xy + yz + xz

让我们看看以下实现以更好地理解 −

示例

 实时演示

class Solution(object):
   def projectionArea(self, grid):
      xy = 0
      yz = 0
      xz = 0
      for r, row in enumerate(grid):
         yz += max(row)
         for c, col in enumerate(row):
            if grid[r][c] > 0:
               xy += 1
            for col in zip(*grid):
               xz += max(col)
      return xy + yz + xz
ob = Solution()
print(ob.projectionArea([[1,2],[3,4]]))

输入

[[1,2],[3,4]]

输出

17

更新于：2020 年 7 月 4 日

431 次浏览

开始您的 职业

通过完成课程获得认证

开始
广告