有理函数与有理数

---

引言

有理数的标准形式可以定义为：被除数和除数之间除了1以外没有其他公因数，且除数为正数。

被除数和除数之间只有一个公因数1。因此可以说，有理数$\mathrm{\frac{1}{3}}$ 处于标准形式。

有理数

要确定一个数是否为有理数，请检查以下条件：它可以表示为$\mathrm{\frac{p}{q}}$的形式，其中q ≠ 0。比率$\mathrm{\frac{p}{q}}$ 已被进一步简化，并且可以表示为十进制格式。

有理函数

有理函数是多项式的比率，其分母多项式不能为零。你知道有理函数被应用于我们日常生活中的各个领域吗？

例如，$\mathrm{g (x) =\frac{(x^2 + x^{-2})}{(2x^2-2x^{-3})}}$ 是一个有理函数，其中 2x²-2x^-3)≠ 0。

众所周知，常数是一个多项式，因为它是一个常数。

有理函数的图像

绘制有理函数图像：

• 用虚线标识并绘制垂直渐近线。

• 用虚线标识并绘制水平渐近线。

• 绘制空洞（如果存在）。

• 绘制所有点，然后连接它们。

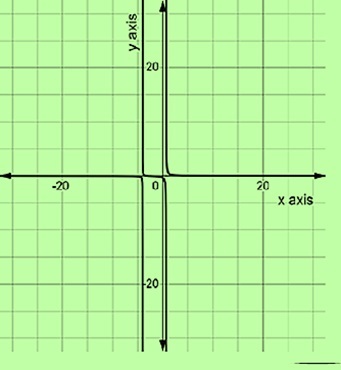
渐近线

有理函数中有三种类型的渐近线：水平渐近线、垂直渐近线和斜渐近线。除此之外，它还可能存在空洞。让我们看看如何找到每一个。

有理函数的空洞

有理函数的空洞似乎存在于有理函数图中，但实际上并不存在。这些可以通过将线性因子（即函数的分子和分母的公因数）设置为零并求解x来获得。您可以通过在一个简化函数中赋值x值来找到点的相应y坐标。并非所有有理函数都需要有空洞。只有当分子和分母具有线性公约数时，才会出现空洞。

有理函数的垂直渐近线

函数的垂直渐近线 (VA) 是一条虚构的垂直线，图形似乎非常接近它，但永远不会接触到它。x = 可以是任何数字格式。这里，“某些数字”与从定义域中排除的值密切相关。但是，请记住，如果x = 数字，如果在相同数字处存在空洞，则可能不存在垂直渐近线。有理函数可以有一个或多个垂直渐近线。要找到有理函数的垂直渐近线：

首先，简化函数以消除公因数（如果存在）。

将分母设置为0并求解 (x)（或等效地获得从定义域中排除的值，避免空洞）

有理函数的水平渐近线

水平渐近线 (HA) 是一条虚构的水平线，图形似乎非常接近它，但永远不会接触到它。y = 任何数字格式。这里，“任意数字”与从值域中排除的值密切相关。找到有理函数的水平渐近线的一种简单方法是使用分子 (N) 和分母 (D) 的阶数。

• 如果 N < D，则 y = 0 有 HA。

• 如果 N > D，则没有 HA。

• 如果 N = D，则 HA 等于 y = 首项系数的比率。

有理函数的斜渐近线

斜渐近线也是一条虚构的斜线，似乎与图形的一部分相切。该方程是使用 y = 长除法将分子除以分母的商。

有理数和有理函数的比较

术语“分数”和“有理数”密切相关，但它们在几个方面有所不同。请注意，“分数总是构成有理数，但有理数可能构成分数，也可能不构成分数”。

分数和有理数的定义

分数是$\mathrm{\frac{a}{b}}$形式的任意数，其中“a”和“b”都是整数，且b ≠ 0。

另一方面，有理数是$\mathrm{\frac{p}{q}}$形式的数，其中“p”和“q”都是整数，q ≠ 0。

因此，分数写成$\mathrm{\frac{m}{n}}$的形式。其中n不为0，m & n为整数（或一个整数）。

例如：23.12、32.10、10.12、21.04。有理数可以表示为$\mathrm{\frac{a}{b}}$的形式。其中b不为0，a & b为整数。例如，$\mathrm{\frac{1}{4},\frac{-9}{2},\frac{-12}{8}}$。

有理分数

• 以有理分数$\mathrm{\frac{a}{b}}$的形式描述。其中a和b为整数，且b ≠ 0。

• 所有分数都是有理数。

• 例如：$\mathrm{\frac{1}{2},\frac{1}{8},\frac{6}{4}}$ 等。

有理数

• 以有理数$\mathrm{\frac{p}{q}}$的形式描述。其中$\mathrm{p,q\in Z}$，q ≠ 0。

• 并非所有有理数都是分数。

• 有理数的例子有$\mathrm{\frac{1}{4},\frac{-9}{2},\frac{-12}{8}}$ 等。

例题解析

1.求反函数：$\mathrm{\mathit{f}(x) =\frac{(2x - 1)}{(x + 3)}}$

解答

已知：

$$\mathrm{y=\frac{(2x - 1)}{(x + 3)}}$$

交换x和y：

$$\mathrm{x=\frac{(2y - 1)}{(y + 3)}}$$

现在：

$$\mathrm{x(y + 3) = 2y - 1}$$

$$\mathrm{xy + 3x = 2y - 1}$$

$$\mathrm{3x + 1 = 2y - xy}$$

$$\mathrm{3x + 1 = y (2 - x)}$$

$$\mathrm{y =\frac{(3x + 1)}{(2 - x)} = \mathit{f}^{-1} (x)}$$

$$$$

$$$$

2. 给定函数$\mathrm{\mathit{f}(x) =\frac{2 (x + 3)}{(x + 3)}+[\frac{1}{(x +3)}]}$。说明其是否为有理函数并说明理由。

解答

这里，函数为：

$$\mathrm{\mathit{f}(x) =\frac{2 (x + 3)}{(x + 3)}+[\frac{1}{(x +3)}]}$$

$$\mathrm{=\frac{2x + 7}{(x + 3)}}$$

$\mathrm{=\frac{p(x)}{q(x)}}$，这里，p(x) 和 q(x) 都是多项式。

结论

在数学中，有理数是我们在学习中最常见的数类型之一，紧随整数之后。“Ratio”（比率）正是它的名称来源。因此，有理数与比率的概念有着密切的联系。

有理数的形式为$\mathrm{\frac{p}{q}}$，其中p和q都是整数，且q不为零。Q是rational number（有理数）的缩写。

$\mathrm{\frac{p}{q}}$形式的数字使得区分分数和有理数变得困难。分数由整数构成，而有理数的分子和分母由整数构成。

常见问题

1. 分数是有理数吗？

所有分数都是有理数，但并非所有有理数都是分数。

2. 区分有理分数和有理数？

分数用整数比率 a/b 表示，其中 b ≠ 0。

有理数用比率 p/q 表示。其中分子和分母是整数，q ≠ 0。

3. 有理数和分数的例子是什么？

有理数的例子有$\mathrm{\frac{1}{4},\frac{-9}{2},\frac{-12}{8}}$等等。分数的例子有$\mathrm{\frac{1}{2},\frac{1}{8},\frac{6}{4}}$等等。

4. 举出真分数和假分数的例子。

真分数是指分母大于分子的分数。例如，$\mathrm{\frac{1}{2},\frac{1}{3},\frac{1}{4}}$ 等。假分数是指分子大于分母的分数，例如 $\mathrm{\frac{3}{2},\frac{5}{4},\frac{7}{6}}$ 等。

5. 两个有理数$\mathrm{\frac{2}{5}}$和$\mathrm{\frac{-3}{4}}$中哪个更大？

给定的有理数是$\mathrm{\frac{2}{5}}$和$\mathrm{\frac{-3}{4}}$。我们清楚地知道，在正有理数和负有理数之间，正有理数总是更大。因此，$\mathrm{\frac{2}{5}}$大于$\mathrm{\frac{-3}{4}}$。