自反关系

---

介绍

自反关系是集合元素之间的一种关系，其中每个元素都与集合中的其他元素相关。顾名思义，集合的每个组成部分都有一个自身的反身像。在集合论中，自反关系是一个重要的概念。“是…的子集”关系在一个集合的集合上就是一个自反关系的例子，因为每个集合都是它自身的子集。

在离散数学中，我们探索各种关系，包括自反的、传递的、对称的等等。在本课中，我们将理解自反关系的概念以及计算有多少自反关系的公式，并通过一些已解决的例子来说明。

什么是关系？

在数学中，两个集合的组成部分之间的映射称为关系。它们有助于将一个集合（定义域）中的元素映射到另一个集合（值域）中的元素，从而产生(输入, 输出)类型的有序对。

假设X和Y是两个集合。设x是集合X中的一个元素，y是集合Y中的一个元素。则所有可能的有序对(x, y)的集合构成了X和Y的笛卡尔积，记作$\mathrm{X\:\times\:Y}$。换句话说，关系说明每个输入都将产生一个或多个输出。

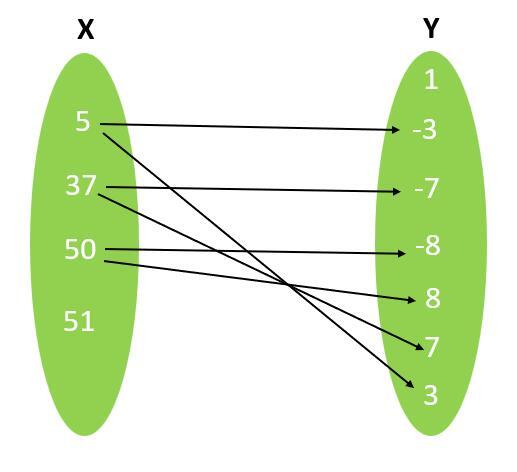
例如 - 假设有两个集合，X = { 5, 37, 50, 51 } 和 Y ={ 1, -3, -7, -8, 8, 7, 3 }。可以用有序对来表示关系，例如“(x, y)属于关系R”，R = {(5, -3), (5, 3), (37, -7), (37, 7), (50, -8), (50, 8)}。

关系的类型

共有八种不同类型的关系，包括：

• 空关系

• 全关系

• 恒等关系

• 逆关系

• 自反关系

• 对称关系

• 传递关系

• 等价关系

自反关系

如果对于在集合A上定义的二元关系R中的每一个元素‘a’，都有aRa，或$\mathrm{\lgroup\:a\:,\:a\:\rgroup\varepsilon\:R}$，则该关系被称为自反关系。根据定义，在一个集合上定义的关系是自反关系，当且仅当该集合的每个元素都与其自身相关。如果集合包含一个不与其自身相关的单个元素，则R不是自反关系。例如，如果对于$\mathrm{b\:\varepsilon\:A}$，b不与其自身相关（表示为$\mathrm{\lgroup\:b\:,\:b\:\rgroup\varepsilon\:R}$ 或“非bRb”），则R不是自反的。

$\mathrm{I_{A}\:=\:\lbrace\:\lgroup\:a\:,\:a\:\rgroup\:\colon\:a\:\varepsilon\:A\:\rbrace}$是另一种在集合A上表示自反关系的方式，其中$\mathrm{I_{A}\:\subseteq\:R}$，而R是在集合A上定义的关系。

让我们来看一个例子。假设$\mathrm{}A\:=\:\lbrace\:a\:,\:b\:,\:c\:,\:d\:,\:e\:\rbrace$，并且R是在A上定义的关系，$\mathrm{R\:=\:\lbrace\:(a\:,\:a)\:,\:(b\:,\:c)\:,\:(d\:,\:e)\:,\:(c\:,\:e)\:,\:(b\:,\:b)\:,\:(c\:,\:c)\:,\:(d\:,\:d)\:,\:(e\:,\:e)\:\rbrace}$。由于$\mathrm{\:(a\:,\:a)\:,\:(b\:,\:b)\:,\:(c\:,\:c)\:,\:(d\:,\:d)\:,\:and\:(e\:,\:e)\:\varepsilon\:R}$，A的每个元素都与其自身相关，因此R是一个自反关系。

在一个有'n'个元素的集合上，自反关系的数量由下式给出：

$$\mathrm{N\:=\:2^{n\:(n\:-\:1)}}$$

其中n是集合中元素的数量，N是自反关系的数量。

自相关元素

自反关系是这样一种关系，其中每个元素都映射到自身。“每个元素都与其自身相关”。

设R是在集合A上定义的关系。给定R是一个自反关系，

$$\mathrm{R\:=\:\lbrace\:\lgroup\:a\:,\:a\:\rgroup\:/\:for\:all\:a\:\varepsilon\:A\:\rbrace}$$

这意味着A的每个元素都必须与其自身相关。

例如，如果A= { 2, 4, 6 }，并且在集合A上定义的R为R = { (2, 2), (4, 4), (6, 6) }。当我们查看R的有序对时，我们发现以下关系。

$\mathrm{(2\:,\:2)\:-------->\:2}$ 2与2相关

$\mathrm{(4\:,\:4)\:-------->\:4}$ 4与4相关

$\mathrm{(6\:,\:6)\:-------->\:6}$ 6与6相关

这就是A的每个元素都与其自身相关的方式，因此集合A的所有元素都是我们的自相关元素。

已解决的例子

1) 当且仅当3a + 7b能被10整除时，在整数集Z上定义关系R为aRb。验证R的自反性。

答案 -

对于$\mathrm{a\:\varepsilon\:Z}$，$\mathrm{3a\:+\:7a\:=\:10a}$，能被10整除。

$\mathrm{\Longrightarrow\:aRa.}$ 由于a可以是Z的任何元素，因此对于所有$\mathrm{a\:\varepsilon\:Z}$，$\mathrm{\lgroup\:a\:,\:a\:\rgroup\:\varepsilon\:R}$。

因此，R是一个自反关系。

因此，当且仅当$\mathrm{3a\:+\:7b}$能被10整除时，在Z上定义的关系R为aRb是自反的。

2) 如果且仅当$\mathrm{a\geq\:b}$时，在自然数集N上定义关系R为aRb。检查R是否是自反关系。

答案 -

答案是：对于$\mathrm{a\:\varepsilon\:N}$，$\mathrm{a\:=\:a}$满足$\mathrm{a\geq\:a}$。

$\mathrm{\Longrightarrow\:aRa.}$ 由于a是N的任意元素，所以对于所有$\mathrm{a\:\varepsilon\:N}$，$\mathrm{\lgroup\:a\:,\:a\:\rgroup\:\varepsilon\:R}$，因为a是N的任意元素。

因此，R是自反的。

3: 考虑集合A，其中关系R定义为'xRy当且仅当$\mathrm{3x\:+\:5y}$能被4整除，对于$\mathrm{x\:,\:y\:\varepsilon\:A}$。证明R是集合A上的自反关系。

答案 -

假设$\mathrm{x\:\varepsilon\:A}$

由于$\mathrm{3x\:+\:5x\:=\:8x}$，它能被4整除。

对于所有x，xRx都成立。

因此，R是自反的。

结论

• 在数学中，两个集合的组成部分之间的映射称为关系。

• 关系有助于将一个集合（定义域）中的元素映射到另一个集合（值域）中的元素，从而产生(输入, 输出)类型的有序对。

• 如果对于在集合A上定义的二元关系R中的每一个元素‘a’，都有aRa，或$\mathrm{\lgroup\:a\:,\:a\:\rgroup\:\varepsilon\:R}$，则该关系被称为自反关系。

• $\mathrm{I_{A}\:=\:\lbrace\:\lgroup\:a\:,\:a\:\rgroup\:\colon\:a\:\varepsilon\:A}$是另一种在集合A上表示自反关系的方式，其中$\mathrm{I_{A}\:\subseteq\:R}$，而R是在集合A上定义的关系。

• 如果集合包含一个不与其自身相关的单个元素，则R不是自反关系。

• 在一个有'n'个元素的集合上，自反关系的数量由下式给出：

$$\mathrm{N\:=\:2^{n\:(n\:-\:1)}}$$

其中n是集合中元素的数量，N是自反关系的数量。

常见问题

1. 数学中的“关系”是什么意思？

在数学中，两个集合的组成部分之间的映射称为关系。它们有助于将一个集合（定义域）中的元素映射到另一个集合（值域）中的元素，从而产生(输入, 输出)类型的有序对。

2. 关系方程是什么？

当关系被表示为方程时，就会产生关系方程。关系方程的一个例子是$\mathrm{y\:=\:x^{2}}$。该关系的图形将看起来像抛物线。

3. 如何计算自反关系的数量？

在一个有'n'个元素的集合上，自反关系的数量由下式给出：

$$\mathrm{N\:=\:2^{n\:(n\:-\:1)}}$$

其中n是集合中元素的数量，N是自反关系的数量。

4. 自反关系的数学概念是什么意思？

如果对于在集合A上定义的二元关系R中的每一个元素a，都有aRa，或$\mathrm{\lgroup\:a\:,\:a\:\rgroup\:\:\varepsilon\:R}$，则该关系被称为自反关系。根据定义，在一个集合上定义的关系是自反关系，当且仅当该集合的每个元素都与其自身相关。

5. 不自反关系和自反关系有什么区别？

如果集合的每个元素都与其自身相关，则A上的二元关系被称为自反关系。如果集合A中至少有一个元素不与其自身相关，则在该集合上定义的关系R被称为非自反关系。