数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会研究
服装研究
法律研究使用 C++ 查找集合中自反关系的数量
在本文中，我们将解释查找集合中自反关系数量的方法。在这个问题中，我们给定一个数字 n，在一个包含 n 个自然数的集合上，我们必须确定自反关系的数量。
自反关系 - 集合 A 中的关系如果对于每个属于集合 A 的 'a'，(a, a) 都属于 R，则称为自反关系。例如 -
Input : x = 1
Output : 1
Explanation : set = { 1 }, reflexive relations on A * A :
{ { 1 } }
Input : x = 2
Output : 4
Explanation : set = { 1,2 }, reflexive relations on A * A :
{ ( 1, 1 ) , ( 2, 2 ) }
{ ( 1, 1 ), ( 2, 2 ), ( 1, 2 ) }
{ ( 1, 1 ), ( 2, 2 ), ( 1, 2 ), ( 2, 1 ) }
{ ( 1, 1 ), ( 2, 2 ), ( 2, 1 ) }因此，如果 (a, a) ∈ R ∀ a ∈ A，则关系是自反的。
查找解决方案的方法
集合元素的自反关系数量可以用公式 2n(n-1) 计算。这个通用公式是通过计算整数的自反关系的数量生成的。
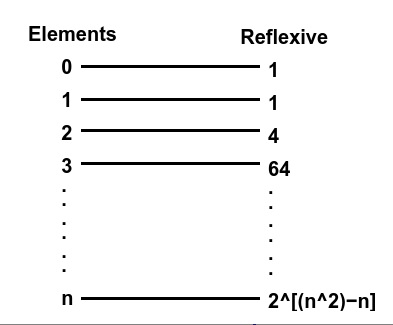
示例
#include <iostream>
using namespace std;
int countReflexive(int n){
int ans = 1 << (n*n - n);
return ans;
}
int main(){
int n ;
cin >> n ; // taking input n from the user using std cin.
int result = countReflexive(n); // calling function to calculate number of reflexive relations
cout << "Number of reflexive relations on set: " << result ; // printing the answer
return 0;
}输出
Number of reflexive relations on set: 1
上述程序的解释
这个程序很容易理解，因为我们只是从用户那里获取输入并将其放入公式 2n(n-1) 中，我们使用左移 "<" 运算符来计算公式，此代码的时间复杂度为 O(1)，随着 n 大小增加而变慢。
结论
在本文中，我们解决了一个问题，即查找集合中自反关系的数量。我们讨论了使用公式计算自反关系数量的简单方法，该公式由数学家推导得出。
我们还学习了针对此问题的 C++ 程序，通过该程序我们找到了时间复杂度为 O(1) 的解决方案。我们可以使用 C、Java、Python 等其他语言编写相同的程序。
更新于：2021年11月24日
435 次浏览
广告