
视线角与轨道摄动
如果地球站位于卫星正下方,则将接收最大信号电平。否则,将无法接收最大信号电平,并且随着地球站经纬度差异的增加,信号电平会降低。
因此,根据需求,我们可以将卫星放置在特定轨道上。现在,让我们讨论一下视线角。
视线角
地球站天线的以下两个角度组合在一起称为视线角。
- 方位角
- 仰角
通常,对于非地球同步轨道,这些角度的值会发生变化。而对于地球同步轨道,这些角度的值不会发生变化。因为,地球同步轨道上的卫星相对于地球看起来是静止的。
这两个角度有助于从地球站天线直接指向卫星。因此,地球站天线的最大增益可以指向卫星。
我们可以使用地球站的经度和纬度以及卫星轨道的方位来计算地球同步轨道的视线角。
方位角
地球站、卫星和地心所经过的平面与当地水平面之间的角度称为方位角。
方位角 ($\alpha$) 的公式为
$$\alpha\: = 180^0 + Tan^{-1}\left(\frac{Tan G}{TanL}\right)$$
其中,
L 是地球站天线的纬度。
G 是卫星轨道位置与地球站天线位置之间的差值。
下图显示了方位角。
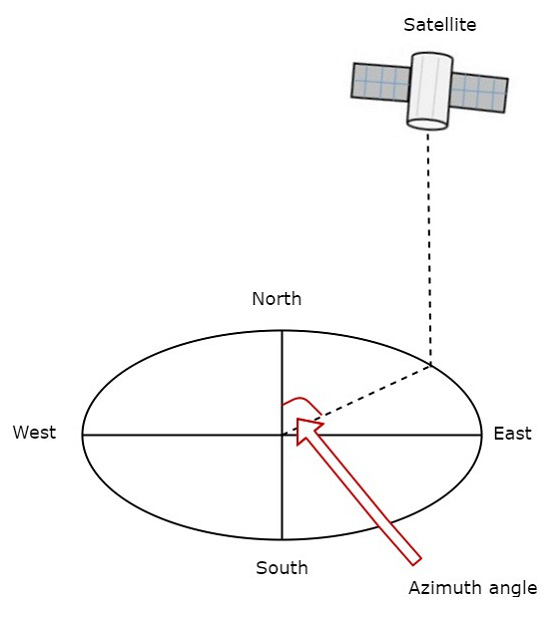
如图所示,测量地球站天线到北极的水平角。它代表方位角。它用于水平跟踪卫星。
仰角
指向卫星的直线与垂直平面之间的角度称为仰角。垂直平面就是垂直于水平平面的平面。
仰角 ($\beta$) 的公式为
$$\beta = Tan^{-1}\left(\frac{cosG.cosL-0.15}{\sqrt{1-cos^2G.cos^2L}}\right)$$
我们可以使用上述公式计算仰角。下图显示了仰角。
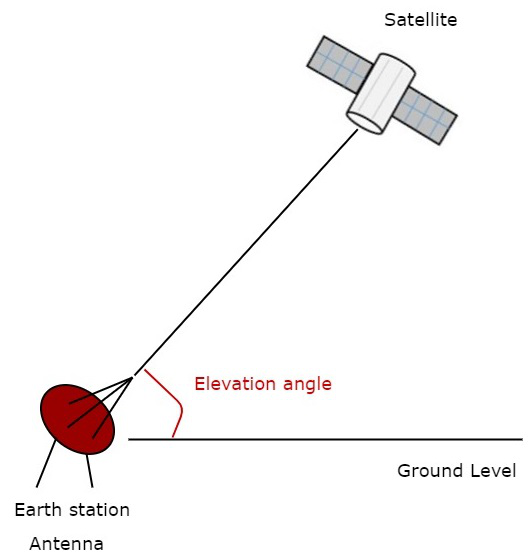
如图所示,测量地球站天线从地面到卫星的垂直角。它代表仰角。
轨道摄动
以下是由于引力和非引力作用或参数引起的轨道摄动。
由于质量分布不均匀,地球周围存在不规则的引力。地球磁场也导致轨道摄动。
主要的外部摄动来自太阳和月亮。当卫星靠近这些外部天体时,它会受到更强的引力。
低轨道卫星会受到与原子和离子碰撞引起的摩擦的影响。
太阳辐射压力会影响使用大型太阳能电池阵列的大型地球同步轨道卫星。
天线发射的射频辐射产生的自生扭矩和压力。
大多数卫星使用推进子系统来维持适当的自旋轴方向并控制卫星对抗扰动力的高度。