卫星通信 - 轨道力学

---

---

我们知道，卫星绕地球运行的路径称为轨道。这条路径可以用数学符号表示。轨道力学是研究存在于轨道上的卫星运动的学科。因此，通过了解轨道运动，我们可以轻松理解空间操作。

轨道要素

轨道要素是描述卫星轨道运动的参数。以下是轨道要素。

• 长半轴
• 偏心率
• 平近点角
• 近地点角距
• 倾角
• 升交点赤经

以上六个轨道要素定义了地球卫星的轨道。因此，可以根据轨道要素的值轻松区分一颗卫星与其他卫星。

长半轴

长半轴 (a)的长度决定了卫星轨道的尺寸。它是长轴的一半。它从中心穿过焦点到椭圆的边缘。因此，它是轨道在轨道两个最远点处的半径。

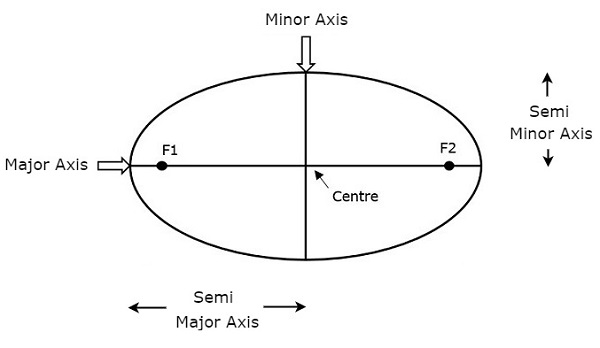
上图显示了长半轴和短半轴。长半轴 (a)的长度不仅决定了卫星轨道的尺寸，还决定了公转周期。

如果将圆形轨道视为一个特例，则长半轴的长度将等于该圆形轨道的半径。

偏心率

偏心率 (e)的值确定了卫星轨道的形状。此参数表示轨道形状与完美圆形的偏差。

如果椭圆轨道的长半轴和短半轴的长度分别为 a 和 b，则偏心率 (e)的数学表达式为

$$e = \frac{\sqrt{a^2 - b^2}}{a}$$

圆形轨道的偏心率值为零，因为 a 和 b 相等。而椭圆轨道的偏心率值介于零和一之间。

下图显示了不同偏心率 (e) 值的各种卫星轨道

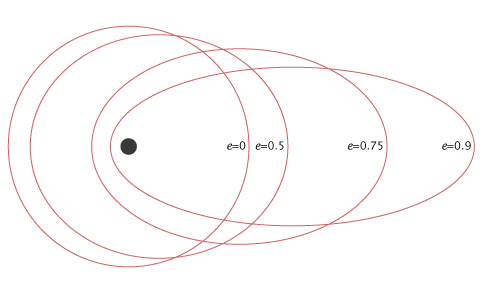
在上图中，对应于偏心率 (e) 值为零的卫星轨道是圆形轨道。其余三个卫星轨道为椭圆形，对应的偏心率 (e) 值分别为 0.5、0.75 和 0.9。

平近点角

对于一颗卫星，距离地球最近的点称为近地点。平近点角 (M) 给出了卫星相对于近地点的角位置的平均值。

如果轨道是圆形的，则平近点角给出卫星在轨道中的角位置。但是，如果轨道是椭圆形的，则计算精确位置非常困难。此时，平近点角用作中间步骤。

近地点角距

卫星轨道在两个点与赤道平面相交。第一个点称为降交点，卫星在此处从北半球穿过南半球。第二个点称为升交点，卫星在此处从南半球穿过北半球。

近地点角距 (ω)是升交点和近地点之间的角度。如果近地点和升交点都存在于同一点，则近地点角距将为零度

近地点角距在地球中心的轨道平面上沿卫星运动方向测量。

倾角

轨道平面和地球赤道平面之间的角度称为倾角 (i)。它在升交点处测量，方向为东向北。因此，倾角以地球赤道为参考定义了轨道的方向。

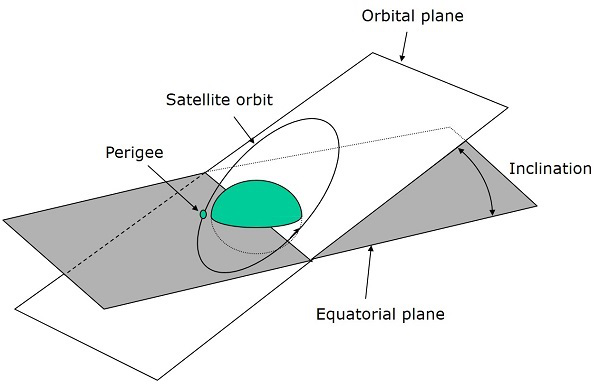
根据倾角，轨道有四种类型。

• 赤道轨道 - 倾角为零度或 180 度。

• 极轨道 - 倾角为 90 度。

• 顺行轨道 - 倾角介于零和 90 度之间。

• 逆行轨道 - 倾角介于 90 和 180 度之间。

升交点赤经

我们知道升交点是卫星从南半球穿过北半球时穿过赤道平面的点。

升交点赤经(Ω)是白羊座线和升交点在赤道平面上的东向角度。白羊座也称为春分点。

卫星的地面轨迹是地球表面上正好位于其轨道正下方的路径。卫星的地面轨迹可以采用多种不同的形式，具体取决于轨道要素的值。

轨道方程

在本节中，让我们讨论与轨道运动相关的方程。

作用在卫星上的力

当卫星绕地球运行时，由于地球的万有引力，它会受到来自地球的拉力。此力称为向心力 (F₁)，因为此力使卫星倾向于向其靠近。

在数学上，由于地球作用在卫星上的向心力 (F₁) 可以写成

$$F_{1} = \frac{GMm}{R^2} $$

其中，

• G 是万有引力常数，等于 6.673 x 10^-11 N∙m²/kg²。

• M 是地球的质量，等于 5.98 x 10²⁴ Kg。

• m 是卫星的质量。

• R 是卫星到地球中心的距离。

当卫星绕地球运行时，由于太阳和月球的万有引力，它会受到来自太阳和月球的拉力。此力称为离心力 (F₂)，因为此力使卫星倾向于远离地球。

在数学上，作用在卫星上的离心力 (F₂) 可以写成

$$F_{2} = \frac{mv^2}{R} $$

其中，v 是卫星的轨道速度。

轨道速度

卫星的轨道速度是卫星绕地球运行的速度。当向心力和离心力平衡时，卫星不会偏离其轨道并以一定速度在该轨道上移动。

因此，使向心力 (F₁) 和离心力 (F₂) 相等。

$$\frac{GMm}{R^2} = \frac{mv^2}{R}$$

$$= > \frac{GM}{R} = v^2$$

$$= > v = \sqrt{\frac{GM}{R}}$$

因此，卫星的轨道速度为

$$v = \sqrt{\frac{GM}{R}}$$

其中，

• G 是万有引力常数，等于 6.673 x 10^-11 N∙m²/kg²。

• M 是地球的质量，等于 5.98 x 10²⁴ Kg。

• R 是卫星到地球中心的距离。

因此，轨道速度主要取决于卫星到地球中心距离 (R)，因为 G 和 M 是常数。