散点图
什么是散点图?
散点图是一种图表,用于显示两组不同数据之间的关系。也称为散点图,它是一种简单直观的表示信息的方式。
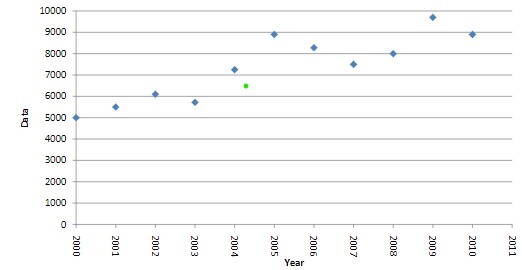
散点图示例
假设您有两组数据,分别是某一组学生学习所花费的小时数以及他们在考试中获得的相应分数。在散点图中,您需要将每个学生的数 据点绘制到图表上。
在图表上,一个轴将表示学习时间,另一个轴表示考试分数。每个学生的数 据点将是一个点,放置在学生学习时间和考试分数的交点处。
现在,如果图表上存在标准模式或趋势,则表明这两个变量之间存在关系。可以观察到,随着学习时间的增加,分数也随之增加。这表明学习时间和考试分数之间存在正相关关系。
另一方面,如果没有特定的模式,并且点散布在整个图表上,则表明这两个变量之间没有明确的关系。这表明学习时间和考试分数之间几乎没有相关性或没有相关性。
散点图的解释
解释散点图需要理解图表中使用的两个变量之间的关系以及它们如何相互关联。
在解释散点图时,需要考虑以下几点 -
关系 - 图表的总体模式说明了两个变量之间的关系。如果存在直线或曲线,则表明变量之间存在关系。例如,如果点从左到右向上移动,则表示正相关关系,这意味着随着一个变量的增加,另一个变量也倾向于增加。相反,如果点从左到右向下移动,则表示负相关关系,这意味着当一个变量增加时,另一个变量会下降。
强度 - 注意点并检查它们如何围绕模式聚集也可以说明两个变量之间关系的强度。当点紧密地位于直线或曲线周围时,表明关系很强。但是,如果点散布开来并且没有遵循任何清晰的模式,则表示两个变量之间存在弱关系或没有关系。
异常值 - 显著远离主要集群的点称为异常值。异常值显示与模式不同步或与大多数数据不同的数据点。异常值会影响变量之间的关系,应检查其重要性。
相关性 - 散点图提供了两个变量之间相关性的视觉反映。如果存在清晰的模式,则表示存在相关性。但是,相关性并不意味着因果关系。也就是说,仅仅因为两个变量相关,并不意味着一个变量是另一个变量变化的原因。
散点图的类型
正散点图 - 正散点图表明两个变量之间存在正相关关系。图表上的点通常倾向于形成向上趋势或模式。此外,随着一个变量的增加,另一个变量也倾向于增加。
负散点图 - 负散点图表示两个变量之间存在负相关关系。在其中,图表上的点通常形成向下趋势或模式。随着一个变量的增加,另一个变量往往会下降。
无相关散点图 - 在无相关散点图中,点之间没有特定的模式。两个变量之间没有直接的关系,这表示几乎没有相关性或没有相关性。
线性散点图 - 线性散点图的点在图表上遵循一条直线。它表明两个变量之间存在线性关系。任何一个变量的变化都会导致另一个变量的成比例变化。
非线性散点图 - 非线性散点图遵循曲线模式。它表示两个变量之间存在非线性关系。在非线性散点图中,变量之间的变化率不成比例或不恒定。
集群散点图 - 集群散点图的图表上的点形成不同的组或集群。这表明数据点属于子组或类别。
如何创建散点图?
收集您的数据 - 第一步是收集两个变量的数据。例如,为了检查考试分数和学习时间之间的关系,必须收集每个学生的对应值。
确定变量 - 根据需要探索的关系的性质,应确定将在 x 轴上绘制的变量以及将在 y 轴上绘制的变量。
设置图表 - 使用数据绘制图表并为每个轴标记。轴必须用适当的标题标记,以表明正在绘制的变量。如果适用,必须包含测量单位。
缩放轴 - 每个轴的范围和间隔应根据数据的数值确定。例如,如果学习时间范围为 0 到 10,考试分数范围为 0 到 100,则必须相应地为每个轴设置适当的刻度。
绘制数据点 - 定位每个数据点在 x 轴和 y 轴上的对应值,并在图表上的该点标记一个点是下一步。这应该对所有数据点执行,以正确地表示每个观察值。
分析散点图 - 应分析点形成的模式。必须检测和检查趋势、集群或异常值。如果变量之间存在关系,并且存在这种关系的性质(正相关、负相关或无相关),则必须建立。
添加任何其他信息 - 可以为散点图添加标题以提供更多上下文,您还可以为多个数据集或类别包含图例。
结论
总的来说,散点图是用于数据分析和可视化的强大工具。它们有助于理解关系、检测模式和异常值,并根据数据做出明智的决策。这就是为什么它们对经济学家很重要的原因。
常见问题
问题 1. 什么是散点图?
答:散点图是一种图表,可以帮助我们了解两组不同数据之间的关系。它是一种简单直观的表示信息的方式。
问题 2. 解释散点图时需要考虑哪些要点?
答:解释散点图时需要考虑的一些要点包括变量的关系、强度、异常值和相关性。
问题 3. 绘制散点图至少需要多少组数据?
答:绘制散点图至少需要两组数据。


 数据结构
数据结构 网络
网络 关系型数据库管理系统
关系型数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP