散点图

---

简介

散点图是一种图表或数学图，它使用笛卡尔坐标系显示数据集的通常两个变量的值。它也被称为散点图、散点图、散点图或散布图。如果点用颜色、形状或大小编码，则可以显示其他变量。数据使用一系列点来表示，每个点的水平轴位置由一个变量的值决定，垂直轴位置由另一个变量的值决定。在本节中，将介绍散点图。

定义

散点图的其他名称包括 XY 图、散点图或散点图。散布图将数值数据对绘制在一个变量在每个轴上的图上，以显示它们之间的关系。当两个连续变量都是独立的，或者当一个连续变量由研究人员控制而另一个变量依赖于它时，可以使用散点图。如果一个参数由另一个参数（也称为自变量或控制参数）定期增加和/或减少，则自变量通常显示在水平轴上。通常，测量或因变量绘制在垂直轴上。如果没有因变量，则任何变量都可以放在任一轴上，散点图仅仅显示两个变量之间相关性的强度，而不是它们之间的因果关系。

图表

散点图可以立即报告大量数据。它在以下情况下很有用：

• 对于大量提供的数

• 每个集合包含两个值。

• 数据以数值形式呈现。

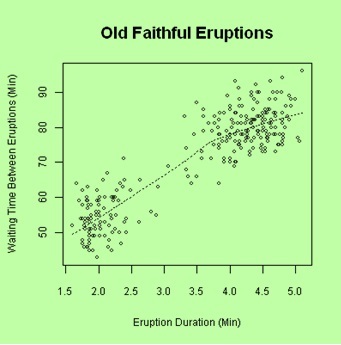
相关性

我们知道，相关性是两个变量的相对运动之间关系的统计量度。如果变量相关，则点将形成一条线或曲线。相关性越好，点越靠近线。这是七种关键质量工具之一的根本原因分析工具。散点图解释了两个特征或变量之间的相关性。它显示了两个变量之间关联的紧密程度。有三种可能的情况来确定两个变量之间的关系

• 正相关 - 两个变量之间的正相关定义为同时或同一方向的运动。当一个变量增加时另一个变量也增加，或者当一个变量减少时另一个变量也减少，则存在正相关。

• 负相关 - 两个变量之间的“负相关”是指一个变量增加时另一个变量减少，反之亦然。

• 无相关性 - 零相关性意味着两个变量之间没有关系。换句话说，当一个变量发生变化时，另一个变量以完全无关的方式发生变化。

用途和示例

散点图用于在水平和垂直轴上绘制数据点，以显示一个变量受另一个变量影响的程度。数据表中每一行的标记位置由 X 和 Y 轴上设置的列值确定。标记的大小或颜色可以分配给第三个变量，从而使地图具有更多维度。术语“相关性”用于表示两个变量之间的关系。如果散点图中的标记几乎彼此平行，则这两个变量具有很强的相关性。如果标记均匀地分散在散点图上，则相关性可以忽略不计或为零。

示例

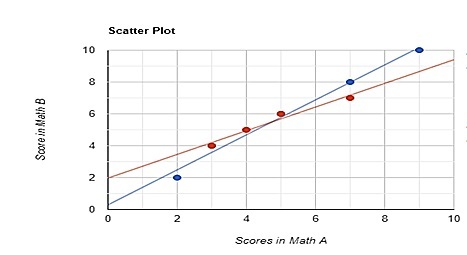
以下是散点图，其中一条直线作为趋势线，显示学生在数学 A 和数学 B 试卷中（满分 10 分）获得的分数。

已解决示例

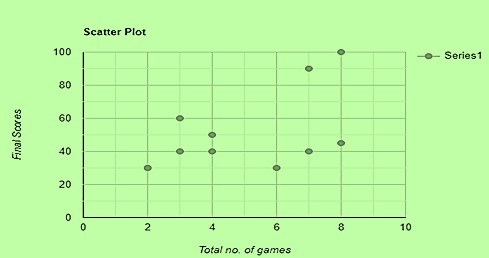
1. 对于以下信息，创建一个散点图，显示每个游戏的总游戏次数 (x) 和最终得分 (y)。

x	2	4	6	7	8	4	2	3	3	7	8
y	30	40	30	40	45	50	30	40	60	90	100

解决方案 -

我们将得分显示在 y 轴上，将比赛次数显示在 x 轴上，以获得上述信息的散点图，如下所示：

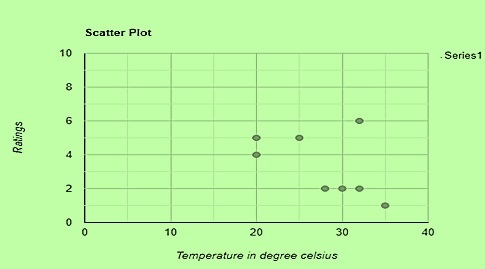
2. 对于以下信息，创建一个散点图，显示白天温度 (x)（摄氏度）和每个交通评级 (y)（满分 10 分）。

x	20	20	25	28	30	32	32	35
y	4	5	5	2	2	2	6	1

解决方案 -

我们将温度 (x)（摄氏度）显示在 x 轴上，将交通评级 (y)（满分 10 分）显示在 y 轴上，以获得上述信息的散点图，如下所示：

结论

• 为了找到两对数值数据之间的关系，散布图将它们绘制在一个变量在每个轴上的图上。如果变量相关，则点将形成一条线或曲线。相关性越好，点越靠近线。

• 我们在以下情况下使用散点图，例如，在尝试确定两个变量之间的关系时，请考虑。在尝试确定潜在问题的根本原因时。在列出潜在的原因和影响后，使用鱼骨图来验证特定原因和影响之间是否存在关联。在确定两个看似相似的现象是否具有相同的原因时，在创建控制图之前，检查自相关。

常见问题解答

1. 散点图的一些常见问题是什么？

散点图的两个主要问题是过度绘制和将相关性误解为因果关系。当数据点太多而无法绘制时，就会发生过度绘制，并且不同的数据点最终会重叠。

2. 散点图显示了哪三件事？

让我们解释一下！它是一个 X-Y 图，说明了两个变量之间的关系。它使用它在垂直和水平轴上绘制数据点。目标是显示一个变量对另一个变量的影响程度。

3. 散点图的理想数据类型是什么？

当比较多个数据点而不考虑时间时，散点图表现最佳。这种类型的图表非常有效地显示了两个变量（由 x 和 y 轴表示）之间的关系，例如一个人的体重和身高。以下是一张此类良好示例的图片。

4. 散点图的局限性是什么？

您无法使用散点图确定关联的确切程度。散点图不会定量地测量变量之间的关系。它只是显示了数量变化在数字上的表达。

5. 散点图显示了多少个变量？

散点图显示了针对相同个体测量的两个数值变量之间的关系。一个变量的值显示在水平轴上，另一个变量的值显示在垂直轴上。图中的每个点都代表数据中的一个个体。