Scikit Learn - 估计器API

上一页
下一页

本章我们将学习估计器API (应用程序编程接口)。让我们首先了解什么是估计器API。

什么是估计器API

它是Scikit-learn实现的主要API之一。它为广泛的机器学习应用提供了一个一致的接口，这就是为什么Scikit-Learn中的所有机器学习算法都是通过估计器API实现的。从数据中学习（拟合数据）的对象是一个估计器。它可以与任何算法一起使用，例如分类、回归、聚类，甚至可以与提取原始数据有用特征的转换器一起使用。

为了拟合数据，所有估计器对象都公开了一个fit方法，该方法接受如下所示的数据集：

estimator.fit(data)

接下来，在通过相应的属性实例化估计器时，可以设置估计器的所有参数，如下所示：

estimator = Estimator (param1=1, param2=2)
estimator.param1

以上输出结果为1。

一旦数据与估计器拟合，就会根据手头的数据估计参数。现在，所有估计的参数都将是估计器对象的属性，并在末尾添加下划线，如下所示：

estimator.estimated_param_

估计器API的用途

估计器的主要用途如下：

模型的估计和解码

估计器对象用于模型的估计和解码。此外，模型被估计为以下内容的确定性函数：

  • 在对象构造中提供的参数。

  • 全局随机状态（numpy.random），如果估计器的random_state参数设置为None。

  • 传递给最近一次调用fit、fit_transform或fit_predict的任何数据。

  • 在一系列调用partial_fit中传递的任何数据。

将非矩形数据表示映射到矩形数据

它将非矩形数据表示映射到矩形数据。简单来说，它接收输入，其中每个样本不表示为固定长度的类似数组的对象，并为每个样本生成一个类似数组的特征对象。

核心样本和异常样本之间的区别

它使用以下方法对核心样本和异常样本之间的区别进行建模：

  • fit

  • 如果为转导式，则为fit_predict

  • 如果为归纳式，则为predict

指导原则

在设计Scikit-Learn API时，考虑了以下指导原则：

一致性

此原则指出，所有对象都应共享一个来自有限方法集的通用接口。文档也应保持一致。

有限的对象层次结构

此指导原则指出：

  • 算法应由Python类表示

  • 数据集应以标准格式表示，例如NumPy数组、Pandas DataFrame、SciPy稀疏矩阵。

  • 参数名称应使用标准Python字符串。

组合

众所周知，机器学习算法可以表示为许多基本算法的序列。Scikit-learn在需要时会使用这些基本算法。

合理的默认值

根据此原则，Scikit-learn库在机器学习模型需要用户指定参数时定义适当的默认值。

检查

根据此指导原则，每个指定的参数值都作为公共属性公开。

使用估计器API的步骤

以下是使用Scikit-Learn估计器API的步骤：

步骤1：选择模型类别

在第一步中，我们需要选择一个模型类别。这可以通过从Scikit-learn导入相应的估计器类来完成。

步骤2：选择模型超参数

在此步骤中，我们需要选择类模型超参数。这可以通过使用所需的值实例化类来完成。

步骤3：排列数据

接下来，我们需要将数据排列到特征矩阵 (X) 和目标向量 (y) 中。

步骤4：模型拟合

现在，我们需要将模型拟合到您的数据。这可以通过调用模型实例的fit()方法来完成。

步骤5：应用模型

拟合模型后，我们可以将其应用于新数据。对于监督学习，使用predict()方法预测未知数据的标签。而对于无监督学习，使用predict()或transform()来推断数据的属性。

监督学习示例

在此，作为此过程的一个示例，我们采用将线拟合到 (x,y) 数据的常见情况，即简单线性回归。

首先，我们需要加载数据集，我们使用的是iris数据集：

示例

import seaborn as sns
iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shape

输出

(150, 4)

示例

y_iris = iris['species']
y_iris.shape

输出

(150,)

示例

现在，对于此回归示例，我们将使用以下样本数据：

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);

输出

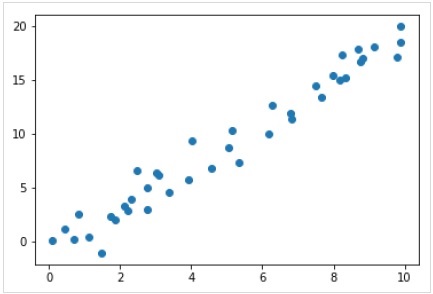
Supervised

因此，我们有上述用于线性回归示例的数据。

现在，使用此数据，我们可以应用上述步骤。

选择模型类别

在这里，为了计算简单的线性回归模型，我们需要导入线性回归类，如下所示：

from sklearn.linear_model import LinearRegression

选择模型超参数

一旦我们选择了一个模型类别，我们就需要做出一些重要的选择，这些选择通常表示为超参数，或者必须在模型拟合到数据之前设置的参数。在这里，对于这个线性回归示例，我们想使用fit_intercept超参数来拟合截距，如下所示：

示例

model = LinearRegression(fit_intercept = True)
model

输出

LinearRegression(copy_X = True, fit_intercept = True, n_jobs = None, normalize = False)

排列数据

现在，正如我们所知，我们的目标变量y处于正确的形式，即长度为n_samples的一维数组。但是，我们需要重塑特征矩阵X，使其成为大小为[n_samples, n_features]的矩阵。这可以通过以下方式完成：

示例

X = x[:, np.newaxis]
X.shape

输出

(40, 1)

模型拟合

一旦我们排列好数据，就该拟合模型了，即，将我们的模型应用于数据。这可以借助fit()方法来完成，如下所示：

示例

model.fit(X, y)

输出

LinearRegression(copy_X = True, fit_intercept = True, n_jobs = None,normalize = False)

在Scikit-learn中，fit()过程有一些尾随下划线。

对于此示例，以下参数显示数据的简单线性拟合的斜率：

示例

model.coef_

输出

array([1.99839352])

以下参数表示对数据的简单线性拟合的截距：

示例

model.intercept_

输出

-0.9895459457775022

将模型应用于新数据

训练模型后，我们可以将其应用于新数据。监督机器学习的主要任务是根据不是训练集一部分的新数据来评估模型。这可以借助predict()方法来完成，如下所示：

示例

xfit = np.linspace(-1, 11)
Xfit = xfit[:, np.newaxis]
yfit = model.predict(Xfit)
plt.scatter(x, y)
plt.plot(xfit, yfit);

输出

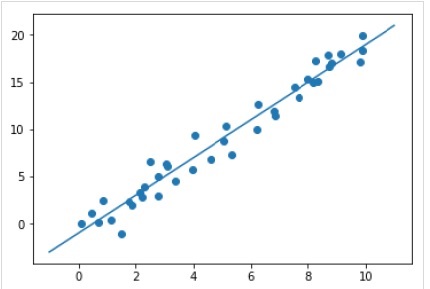
Model New Data

完整的可运行示例

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shape
y_iris = iris['species']
y_iris.shape

rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=True)
model
X = x[:, np.newaxis]
X.shape

model.fit(X, y)
model.coef_
model.intercept_

xfit = np.linspace(-1, 11)
Xfit = xfit[:, np.newaxis]
yfit = model.predict(Xfit)
plt.scatter(x, y)
plt.plot(xfit, yfit);

无监督学习示例

在这里，作为此过程的一个示例，我们采用降低Iris数据集维数的常见情况，以便我们可以更轻松地对其进行可视化。对于此示例，我们将使用主成分分析 (PCA)，这是一种快速的线性降维技术。

与上面给出的示例一样，我们可以加载并绘制来自iris数据集的随机数据。之后，我们可以按照以下步骤操作：

选择模型类别

from sklearn.decomposition import PCA

选择模型超参数

示例

model = PCA(n_components=2)
model

输出

PCA(copy = True, iterated_power = 'auto', n_components = 2, random_state = None,
   svd_solver = 'auto', tol = 0.0, whiten = False)

模型拟合

示例

model.fit(X_iris)

输出

PCA(copy = True, iterated_power = 'auto', n_components = 2, random_state = None,
   svd_solver = 'auto', tol = 0.0, whiten = False)

将数据转换为二维

示例

X_2D = model.transform(X_iris)

现在，我们可以绘制结果，如下所示：

输出

iris['PCA1'] = X_2D[:, 0]
iris['PCA2'] = X_2D[:, 1]
sns.lmplot("PCA1", "PCA2", hue = 'species', data = iris, fit_reg = False);

输出

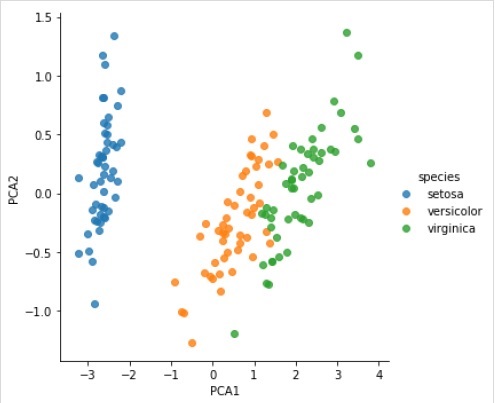
two dimensional

完整的可运行示例

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shape
y_iris = iris['species']
y_iris.shape
rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);
from sklearn.decomposition import PCA

model = PCA(n_components=2)
model
model.fit(X_iris)
X_2D = model.transform(X_iris)
iris['PCA1'] = X_2D[:, 0]
iris['PCA2'] = X_2D[:, 1]
sns.lmplot("PCA1", "PCA2", hue='species', data=iris, fit_reg=False);
打印页面
上一页
下一页
广告