
- Scikit Learn 教程
- Scikit Learn - 首页
- Scikit Learn - 简介
- Scikit Learn - 建模过程
- Scikit Learn - 数据表示
- Scikit Learn - 估计器 API
- Scikit Learn - 约定
- Scikit Learn - 线性模型
- Scikit Learn - 扩展线性模型
- 随机梯度下降
- Scikit Learn - 支持向量机
- Scikit Learn - 异常检测
- Scikit Learn - K 近邻算法
- Scikit Learn - KNN 学习
- 朴素贝叶斯分类
- Scikit Learn - 决策树
- 随机决策树
- Scikit Learn - 集成方法
- Scikit Learn - 聚类方法
- 聚类性能评估
- 使用 PCA 的降维
- Scikit Learn 有用资源
- Scikit Learn 快速指南
- Scikit Learn - 有用资源
- Scikit Learn - 讨论
Scikit Learn 快速指南
Scikit Learn - 简介
在本章中,我们将了解什么是 Scikit-Learn 或 Sklearn,Scikit-Learn 的起源以及其他相关主题,例如负责 Scikit-Learn 的开发和维护的社区和贡献者、它的先决条件、安装及其功能。
什么是 Scikit-Learn (Sklearn)
Scikit-learn (Sklearn) 是 Python 中最有用和最强大的机器学习库。它提供了一系列高效的机器学习和统计建模工具,包括通过 Python 中的一致接口进行分类、回归、聚类和降维。这个库主要用 Python 编写,构建于NumPy、SciPy 和Matplotlib 之上。
Scikit-Learn 的起源
它最初被称为scikits.learn,最初由 David Cournapeau 于 2007 年作为 Google Summer of Code 项目开发。后来,在 2010 年,来自 FIRCA(法国计算机科学与自动化研究所)的 Fabian Pedregosa、Gael Varoquaux、Alexandre Gramfort 和 Vincent Michel 将该项目提升到另一个层次,并在 2010 年 2 月 1 日发布了第一个公开版本(v0.1 beta)。
让我们来看看它的版本历史 -
2019 年 5 月:scikit-learn 0.21.0
2019 年 3 月:scikit-learn 0.20.3
2018 年 12 月:scikit-learn 0.20.2
2018 年 11 月:scikit-learn 0.20.1
2018 年 9 月:scikit-learn 0.20.0
2018 年 7 月:scikit-learn 0.19.2
2017 年 7 月:scikit-learn 0.19.0
2016 年 9 月:scikit-learn 0.18.0
2015 年 11 月:scikit-learn 0.17.0
2015 年 3 月:scikit-learn 0.16.0
2014 年 7 月:scikit-learn 0.15.0
2013 年 8 月:scikit-learn 0.14
社区与贡献者
Scikit-learn 是一个社区项目,任何人都可以为其做出贡献。该项目托管在https://github.com/scikit-learn/scikit-learn。以下人员目前是 Sklearn 开发和维护的核心贡献者 -
Joris Van den Bossche(数据科学家)
Thomas J Fan(软件开发工程师)
Alexandre Gramfort(机器学习研究员)
Olivier Grisel(机器学习专家)
Nicolas Hug(副研究科学家)
Andreas Mueller(机器学习科学家)
Hanmin Qin(软件工程师)
Adrin Jalali(开源开发者)
Nelle Varoquaux(数据科学研究员)
Roman Yurchak(数据科学家)
Booking.com、JP Morgan、Evernote、Inria、AWeber、Spotify 等众多组织都在使用 Sklearn。
先决条件
在我们开始使用 scikit-learn 最新版本之前,我们需要以下内容 -
Python (>=3.5)
NumPy (>= 1.11.0)
Scipy (>= 0.17.0)
Joblib (>= 0.11)
Sklearn 绘图功能需要 Matplotlib (>= 1.5.1)。
使用数据结构和分析的一些 scikit-learn 示例需要 Pandas (>= 0.18.0)。
安装
如果您已经安装了 NumPy 和 Scipy,以下是用两种最简单的方法安装 scikit-learn 的方法 -
使用 pip
可以使用以下命令通过 pip 安装 scikit-learn -
pip install -U scikit-learn
使用 conda
可以使用以下命令通过 conda 安装 scikit-learn -
conda install scikit-learn
另一方面,如果您的 Python 工作站上尚未安装 NumPy 和 Scipy,则可以使用pip 或conda 来安装它们。
使用 scikit-learn 的另一种方法是使用Canopy 和Anaconda 等 Python 发行版,因为它们都附带了 scikit-learn 的最新版本。
功能
Scikit-learn 库不侧重于加载、操作和汇总数据,而是侧重于对数据建模。Sklearn 提供的一些最流行的模型组如下 -
监督学习算法 - 几乎所有流行的监督学习算法,如线性回归、支持向量机 (SVM)、决策树等,都是 scikit-learn 的一部分。
无监督学习算法 - 另一方面,它还包含从聚类、因子分析、PCA(主成分分析)到无监督神经网络的所有流行的无监督学习算法。
聚类 - 此模型用于对未标记数据进行分组。
交叉验证 - 用于检查监督模型在未见数据上的准确性。
降维 - 用于减少数据中属性的数量,可用于汇总、可视化和特征选择。
集成方法 - 顾名思义,它用于组合多个监督模型的预测。
特征提取 - 用于从数据中提取特征以定义图像和文本数据中的属性。
特征选择 - 用于识别有用的属性以创建监督模型。
开源 - 它是一个开源库,也可以在 BSD 许可下商业使用。
Scikit Learn - 建模过程
本章介绍 Sklearn 中涉及的建模过程。让我们详细了解一下,并从数据集加载开始。
数据集加载
数据的集合称为数据集。它包含以下两个组成部分 -
特征 - 数据的变量称为其特征。它们也称为预测变量、输入或属性。
特征矩阵 - 如果有多个特征,则为特征的集合。
特征名称 - 所有特征名称的列表。
响应 - 基本上取决于特征变量的输出变量。它们也称为目标、标签或输出。
响应向量 - 用于表示响应列。通常,我们只有一个响应列。
目标名称 - 表示响应向量可能取的值。
Scikit-learn 有几个示例数据集,例如用于分类的iris 和digits,以及用于回归的波士顿房价。
示例
以下是如何加载iris 数据集的示例 -
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
feature_names = iris.feature_names
target_names = iris.target_names
print("Feature names:", feature_names)
print("Target names:", target_names)
print("\nFirst 10 rows of X:\n", X[:10])
输出
Feature names: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)'] Target names: ['setosa' 'versicolor' 'virginica'] First 10 rows of X: [ [5.1 3.5 1.4 0.2] [4.9 3. 1.4 0.2] [4.7 3.2 1.3 0.2] [4.6 3.1 1.5 0.2] [5. 3.6 1.4 0.2] [5.4 3.9 1.7 0.4] [4.6 3.4 1.4 0.3] [5. 3.4 1.5 0.2] [4.4 2.9 1.4 0.2] [4.9 3.1 1.5 0.1] ]
分割数据集
为了检查模型的准确性,我们可以将数据集分成两部分 -训练集和测试集。使用训练集训练模型,使用测试集测试模型。之后,我们可以评估模型的效果。
示例
下面的示例将数据按 70:30 的比例分割,即 70% 的数据将用作训练数据,30% 的数据将用作测试数据。数据集与上面的示例一样是 iris 数据集。
from sklearn.datasets import load_iris iris = load_iris() X = iris.data y = iris.target from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split( X, y, test_size = 0.3, random_state = 1 ) print(X_train.shape) print(X_test.shape) print(y_train.shape) print(y_test.shape)
输出
(105, 4) (45, 4) (105,) (45,)
如上例所示,它使用 scikit-learn 的train_test_split() 函数分割数据集。此函数具有以下参数 -
X, y - 这里,X 是特征矩阵,y 是响应向量,需要分割。
test_size - 这表示测试数据与总给定数据的比率。在上例中,我们为 X 的 150 行设置test_data = 0.3。它将产生 150*0.3 = 45 行的测试数据。
random_size - 用于保证分割始终相同。这在需要可重复结果的情况下非常有用。
训练模型
接下来,我们可以使用我们的数据集来训练一些预测模型。如前所述,scikit-learn 具有广泛的机器学习 (ML) 算法,这些算法具有用于拟合、预测准确性、召回率等的一致接口。
示例
在下面的示例中,我们将使用 KNN(K 近邻)分类器。不必深入了解 KNN 算法的细节,因为后面会有单独的章节讲解。此示例用于让您了解实现部分。
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size = 0.4, random_state=1
)
from sklearn.neighbors import KNeighborsClassifier
from sklearn import metrics
classifier_knn = KNeighborsClassifier(n_neighbors = 3)
classifier_knn.fit(X_train, y_train)
y_pred = classifier_knn.predict(X_test)
# Finding accuracy by comparing actual response values(y_test)with predicted response value(y_pred)
print("Accuracy:", metrics.accuracy_score(y_test, y_pred))
# Providing sample data and the model will make prediction out of that data
sample = [[5, 5, 3, 2], [2, 4, 3, 5]]
preds = classifier_knn.predict(sample)
pred_species = [iris.target_names[p] for p in preds] print("Predictions:", pred_species)
输出
Accuracy: 0.9833333333333333 Predictions: ['versicolor', 'virginica']
模型持久化
训练模型后,最好使模型持久化以供将来使用,这样我们就不需要反复重新训练它。这可以使用joblib 包的dump 和load 功能来完成。
考虑下面的示例,我们将保存上面训练的模型 (classifier_knn) 以供将来使用 -
from sklearn.externals import joblib joblib.dump(classifier_knn, 'iris_classifier_knn.joblib')
上面的代码会将模型保存到名为 iris_classifier_knn.joblib 的文件中。现在,可以使用以下代码从文件中重新加载该对象 -
joblib.load('iris_classifier_knn.joblib')
数据预处理
由于我们处理大量原始数据,在将数据输入机器学习算法之前,我们需要将其转换为有意义的数据。这个过程称为数据预处理。Scikit-learn 有一个名为preprocessing 的包用于此目的。preprocessing 包具有以下技术 -
二值化
当我们需要将数值转换为布尔值时,使用此预处理技术。
示例
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]]
)
data_binarized = preprocessing.Binarizer(threshold=0.5).transform(input_data)
print("\nBinarized data:\n", data_binarized)
在上例中,我们使用阈值 = 0.5,因此所有大于 0.5 的值将转换为 1,所有小于 0.5 的值将转换为 0。
输出
Binarized data: [ [ 1. 0. 1.] [ 0. 1. 1.] [ 0. 0. 1.] [ 1. 1. 0.] ]
均值移除
此技术用于消除特征向量中的均值,以便每个特征都以零为中心。
示例
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]]
)
#displaying the mean and the standard deviation of the input data
print("Mean =", input_data.mean(axis=0))
print("Stddeviation = ", input_data.std(axis=0))
#Removing the mean and the standard deviation of the input data
data_scaled = preprocessing.scale(input_data)
print("Mean_removed =", data_scaled.mean(axis=0))
print("Stddeviation_removed =", data_scaled.std(axis=0))
输出
Mean = [ 1.75 -1.275 2.2 ] Stddeviation = [ 2.71431391 4.20022321 4.69414529] Mean_removed = [ 1.11022302e-16 0.00000000e+00 0.00000000e+00] Stddeviation_removed = [ 1. 1. 1.]
缩放
我们使用此预处理技术来缩放特征向量。特征向量的缩放很重要,因为特征不应人为地过大或过小。
示例
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]
]
)
data_scaler_minmax = preprocessing.MinMaxScaler(feature_range=(0,1))
data_scaled_minmax = data_scaler_minmax.fit_transform(input_data)
print ("\nMin max scaled data:\n", data_scaled_minmax)
输出
Min max scaled data: [ [ 0.48648649 0.58252427 0.99122807] [ 0. 1. 0.81578947] [ 0.27027027 0. 1. ] [ 1. 0.99029126 0. ] ]
归一化
我们使用此预处理技术来修改特征向量。特征向量的归一化是必要的,以便可以以共同的尺度测量特征向量。归一化有两种类型,如下所示 -
L1 归一化
也称为最小绝对偏差。它以这样的方式修改值,使得每一行中绝对值的总和始终保持为 1。以下示例显示了在输入数据上实现 L1 归一化的过程。
示例
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]
]
)
data_normalized_l1 = preprocessing.normalize(input_data, norm='l1')
print("\nL1 normalized data:\n", data_normalized_l1)
输出
L1 normalized data: [ [ 0.22105263 -0.2 0.57894737] [-0.2027027 0.32432432 0.47297297] [ 0.03571429 -0.56428571 0.4 ] [ 0.42142857 0.16428571 -0.41428571] ]
L2 归一化
也称为最小二乘法。它以这样的方式修改值,使得每一行的平方和始终保持为1。以下示例显示了在输入数据上实现L2归一化的过程。
示例
import numpy as np
from sklearn import preprocessing
Input_data = np.array(
[
[2.1, -1.9, 5.5],
[-1.5, 2.4, 3.5],
[0.5, -7.9, 5.6],
[5.9, 2.3, -5.8]
]
)
data_normalized_l2 = preprocessing.normalize(input_data, norm='l2')
print("\nL1 normalized data:\n", data_normalized_l2)
输出
L2 normalized data: [ [ 0.33946114 -0.30713151 0.88906489] [-0.33325106 0.53320169 0.7775858 ] [ 0.05156558 -0.81473612 0.57753446] [ 0.68706914 0.26784051 -0.6754239 ] ]
Scikit Learn - 数据表示
众所周知,机器学习是关于从数据中创建模型的。为此,计算机必须首先理解数据。接下来,我们将讨论各种表示数据的方法,以便计算机能够理解——
数据表示为表格
在Scikit-learn中表示数据的最佳方法是表格形式。表格表示一个二维数据网格,其中行代表数据集的单个元素,列代表与这些单个元素相关的量。
示例
通过以下示例,我们可以使用python的seaborn库,将iris数据集下载为Pandas DataFrame的形式。
import seaborn as sns
iris = sns.load_dataset('iris')
iris.head()
输出
sepal_length sepal_width petal_length petal_width species 0 5.1 3.5 1.4 0.2 setosa 1 4.9 3.0 1.4 0.2 setosa 2 4.7 3.2 1.3 0.2 setosa 3 4.6 3.1 1.5 0.2 setosa 4 5.0 3.6 1.4 0.2 setosa
从上面的输出中,我们可以看到数据的每一行代表一朵观察到的花,行数代表数据集中花的总数。通常,我们将矩阵的行称为样本。
另一方面,数据的每一列代表描述每个样本的定量信息。通常,我们将矩阵的列称为特征。
数据作为特征矩阵
特征矩阵可以定义为表格布局,其中信息可以被认为是一个二维矩阵。它存储在一个名为X的变量中,并假设它是一个二维矩阵,形状为[n_samples, n_features]。它通常包含在NumPy数组或Pandas DataFrame中。如前所述,样本始终代表数据集描述的单个对象,而特征则以定量方式描述每个样本的不同观察结果。
数据作为目标数组
除了用X表示的特征矩阵外,我们还有目标数组。它也称为标签,用y表示。标签或目标数组通常是一维的,长度为n_samples。它通常包含在NumPy array或Pandas Series中。目标数组可以同时具有连续数值和离散值。
目标数组与特征列有何不同?
我们可以通过一点来区分两者,即目标数组通常是我们想要从数据中预测的量,即在统计术语中它是因变量。
示例
在下面的例子中,从iris数据集中,我们根据其他测量结果来预测花的种类。在这种情况下,Species列将被视为特征。
import seaborn as sns
iris = sns.load_dataset('iris')
%matplotlib inline
import seaborn as sns; sns.set()
sns.pairplot(iris, hue='species', height=3);
输出
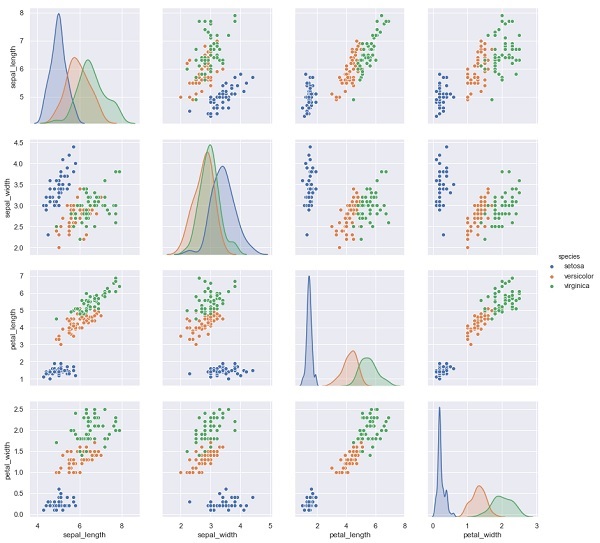
X_iris = iris.drop('species', axis=1)
X_iris.shape
y_iris = iris['species']
y_iris.shape
输出
(150,4) (150,)
Scikit Learn - 估计器 API
在本章中,我们将学习估计器API(应用程序编程接口)。让我们从了解什么是估计器API开始。
什么是估计器API
它是Scikit-learn实现的主要API之一。它为广泛的机器学习应用提供了一个一致的接口,这就是为什么Scikit-Learn中的所有机器学习算法都是通过估计器API实现的。从数据中学习(拟合数据)的对象是一个估计器。它可以与任何算法一起使用,例如分类、回归、聚类,甚至与转换器一起使用,转换器可以从原始数据中提取有用的特征。
为了拟合数据,所有估计器对象都公开了一个fit方法,如下所示:
estimator.fit(data)
接下来,所有估计器的参数都可以在实例化时通过相应的属性设置,如下所示。
estimator = Estimator (param1=1, param2=2) estimator.param1
上述结果将为1。
一旦数据与估计器拟合,参数就会根据现有的数据进行估计。现在,所有估计的参数都将是估计器对象的属性,以下划线结尾,如下所示:
estimator.estimated_param_
估计器API的用途
估计器的主要用途如下:
模型的估计和解码
估计器对象用于模型的估计和解码。此外,模型被估计为以下内容的确定性函数:
在对象构造中提供的参数。
如果估计器的random_state参数设置为None,则为全局随机状态(numpy.random)。
传递给最近一次调用fit、fit_transform或fit_predict的任何数据。
传递给一系列partial_fit调用的任何数据。
将非矩形数据表示映射到矩形数据
它将非矩形数据表示映射到矩形数据。简单来说,它接收输入,其中每个样本不表示为固定长度的类似数组的对象,并为每个样本生成一个类似数组的特征对象。
核心样本和异常样本之间的区别
它使用以下方法对核心样本和异常样本之间的区别进行建模:
fit
如果为转导式,则为fit_predict
如果为归纳式,则为predict
指导原则
在设计Scikit-Learn API时,考虑了以下指导原则:
一致性
此原则指出,所有对象都应共享一个从有限方法集中提取的通用接口。文档也应该保持一致。
有限的对象层次结构
此指导原则指出:
算法应由Python类表示。
数据集应以标准格式表示,例如NumPy数组、Pandas DataFrame、SciPy稀疏矩阵。
参数名称应使用标准Python字符串。
组合
众所周知,机器学习算法可以表示为许多基本算法的序列。Scikit-learn在需要时会使用这些基本算法。
合理的默认值
根据此原则,Scikit-learn库在机器学习模型需要用户指定参数时定义一个合适的默认值。
检查
根据此指导原则,每个指定的参数值都作为公共属性公开。
使用估计器API的步骤
以下是使用Scikit-Learn估计器API的步骤:
步骤1:选择模型类别
在第一步中,我们需要选择一个模型类别。这可以通过从Scikit-learn导入相应的估计器类来完成。
步骤2:选择模型超参数
在此步骤中,我们需要选择类模型超参数。这可以通过使用所需的值实例化类来完成。
步骤3:整理数据
接下来,我们需要将数据整理成特征矩阵(X)和目标向量(y)。
步骤4:模型拟合
现在,我们需要将模型拟合到您的数据。这可以通过调用模型实例的fit()方法来完成。
步骤5:应用模型
拟合模型后,我们可以将其应用于新数据。对于监督学习,使用predict()方法预测未知数据的标签。而对于无监督学习,使用predict()或transform()来推断数据的属性。
监督学习示例
在这里,作为此过程的一个示例,我们采用将直线拟合到(x,y)数据(即简单线性回归)的常见情况。
首先,我们需要加载数据集,我们使用iris数据集:
示例
import seaborn as sns
iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shape
输出
(150, 4)
示例
y_iris = iris['species'] y_iris.shape
输出
(150,)
示例
现在,对于这个回归示例,我们将使用以下样本数据:
%matplotlib inline import matplotlib.pyplot as plt import numpy as np rng = np.random.RandomState(35) x = 10*rng.rand(40) y = 2*x-1+rng.randn(40) plt.scatter(x,y);
输出
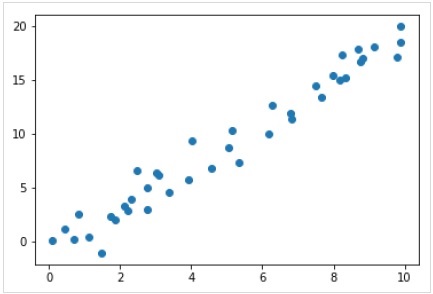
因此,我们有上述数据用于我们的线性回归示例。
现在,使用此数据,我们可以应用上述步骤。
选择模型类别
在这里,为了计算简单的线性回归模型,我们需要导入线性回归类,如下所示:
from sklearn.linear_model import LinearRegression
选择模型超参数
一旦我们选择了一个模型类别,我们需要做出一些重要的选择,这些选择通常表示为超参数,或者必须在模型拟合到数据之前设置的参数。在这里,对于这个线性回归示例,我们想使用fit_intercept超参数来拟合截距,如下所示:
示例
model = LinearRegression(fit_intercept = True) model
输出
LinearRegression(copy_X = True, fit_intercept = True, n_jobs = None, normalize = False)
整理数据
现在,我们知道我们的目标变量y处于正确的形式,即长度为n_samples的一维数组。但是,我们需要重塑特征矩阵X,使其成为大小为[n_samples, n_features]的矩阵。这可以如下完成:
示例
X = x[:, np.newaxis] X.shape
输出
(40, 1)
模型拟合
一旦我们整理好数据,就该拟合模型了,即,将我们的模型应用于数据。这可以借助fit()方法完成,如下所示:
示例
model.fit(X, y)
输出
LinearRegression(copy_X = True, fit_intercept = True, n_jobs = None,normalize = False)
在Scikit-learn中,fit()过程有一些尾随下划线。
对于此示例,以下参数显示了数据简单线性拟合的斜率:
示例
model.coef_
输出
array([1.99839352])
以下参数表示对数据的简单线性拟合的截距:
示例
model.intercept_
输出
-0.9895459457775022
将模型应用于新数据
训练模型后,我们可以将其应用于新数据。监督机器学习的主要任务是根据不是训练集一部分的新数据来评估模型。这可以借助predict()方法完成,如下所示:
示例
xfit = np.linspace(-1, 11) Xfit = xfit[:, np.newaxis] yfit = model.predict(Xfit) plt.scatter(x, y) plt.plot(xfit, yfit);
输出
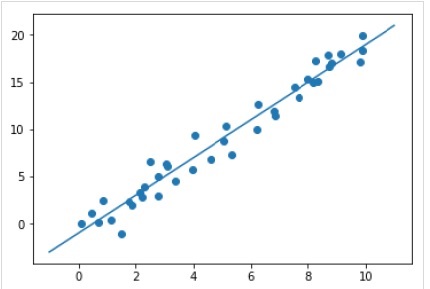
完整的可运行示例
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shape
y_iris = iris['species']
y_iris.shape
rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=True)
model
X = x[:, np.newaxis]
X.shape
model.fit(X, y)
model.coef_
model.intercept_
xfit = np.linspace(-1, 11)
Xfit = xfit[:, np.newaxis]
yfit = model.predict(Xfit)
plt.scatter(x, y)
plt.plot(xfit, yfit);
无监督学习示例
在这里,作为此过程的一个示例,我们采用降低Iris数据集维数的常见情况,以便我们可以更轻松地对其进行可视化。对于此示例,我们将使用主成分分析 (PCA),这是一种快速的线性降维技术。
像上面给出的示例一样,我们可以加载并绘制来自iris数据集的随机数据。之后,我们可以按照以下步骤操作:
选择模型类别
from sklearn.decomposition import PCA
选择模型超参数
示例
model = PCA(n_components=2) model
输出
PCA(copy = True, iterated_power = 'auto', n_components = 2, random_state = None, svd_solver = 'auto', tol = 0.0, whiten = False)
模型拟合
示例
model.fit(X_iris)
输出
PCA(copy = True, iterated_power = 'auto', n_components = 2, random_state = None, svd_solver = 'auto', tol = 0.0, whiten = False)
将数据转换为二维
示例
X_2D = model.transform(X_iris)
现在,我们可以绘制结果,如下所示:
输出
iris['PCA1'] = X_2D[:, 0]
iris['PCA2'] = X_2D[:, 1]
sns.lmplot("PCA1", "PCA2", hue = 'species', data = iris, fit_reg = False);
输出
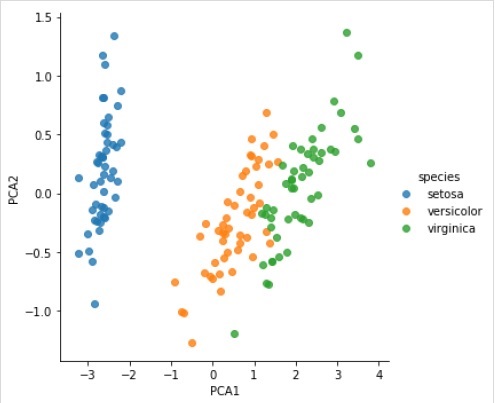
完整的可运行示例
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
iris = sns.load_dataset('iris')
X_iris = iris.drop('species', axis = 1)
X_iris.shape
y_iris = iris['species']
y_iris.shape
rng = np.random.RandomState(35)
x = 10*rng.rand(40)
y = 2*x-1+rng.randn(40)
plt.scatter(x,y);
from sklearn.decomposition import PCA
model = PCA(n_components=2)
model
model.fit(X_iris)
X_2D = model.transform(X_iris)
iris['PCA1'] = X_2D[:, 0]
iris['PCA2'] = X_2D[:, 1]
sns.lmplot("PCA1", "PCA2", hue='species', data=iris, fit_reg=False);
Scikit Learn - 约定
Scikit-learn的对象共享一个统一的基本API,它包含以下三个互补接口:
估计器接口 - 用于构建和拟合模型。
预测器接口 - 用于进行预测。
转换器接口 - 用于转换数据。
这些API采用简单的约定,设计选择以避免框架代码的激增为指导。
约定的目的
约定的目的是确保API遵循以下广泛的原则:
一致性 - 所有对象,无论是基本对象还是复合对象,都必须共享一个一致的接口,该接口进一步由有限的一组方法组成。
检查 - 构造函数参数和学习算法确定的参数值应存储并作为公共属性公开。
避免类激增 - 数据集应表示为NumPy数组或Scipy稀疏矩阵,而超参数名称和值应表示为标准Python字符串,以避免框架代码的激增。
组合 - 无论算法是表示为数据转换的序列或组合,还是自然地被视为参数化在其他算法上的元算法,都应使用现有的构建块进行实现和组合。
合理的默认值 - 在scikit-learn中,每当操作需要用户定义的参数时,都会定义一个合适的默认值。此默认值应导致操作以合理的方式执行,例如,为手头的任务提供基线解决方案。
各种约定
Sklearn中可用的约定解释如下:
类型转换
文档说明输入应转换为float64类型。以下示例将解释如何使用sklearn.random_projection模块降低数据的维度。
示例
import numpy as np from sklearn import random_projection rannge = np.random.RandomState(0) X = range.rand(10,2000) X = np.array(X, dtype = 'float32') X.dtype Transformer_data = random_projection.GaussianRandomProjection() X_new = transformer.fit_transform(X) X_new.dtype
输出
dtype('float32')
dtype('float64')
在上述示例中,我们可以看到X是float32类型,通过fit_transform(X)转换为float64类型。
重新拟合和更新参数
估计器的超参数可以在构造后通过set_params()方法更新和重新拟合。让我们看下面的例子来理解它。
示例
import numpy as np from sklearn.datasets import load_iris from sklearn.svm import SVC X, y = load_iris(return_X_y = True) clf = SVC() clf.set_params(kernel = 'linear').fit(X, y) clf.predict(X[:5])
输出
array([0, 0, 0, 0, 0])
估计器构造完成后,上面的代码将通过SVC.set_params()将默认内核rbf更改为线性。
现在,下面的代码将把内核改回rbf以重新拟合估计器并进行第二次预测。
示例
clf.set_params(kernel = 'rbf', gamma = 'scale').fit(X, y) clf.predict(X[:5])
输出
array([0, 0, 0, 0, 0])
完整代码
以下是完整的可执行程序。
import numpy as np from sklearn.datasets import load_iris from sklearn.svm import SVC X, y = load_iris(return_X_y = True) clf = SVC() clf.set_params(kernel = 'linear').fit(X, y) clf.predict(X[:5]) clf.set_params(kernel = 'rbf', gamma = 'scale').fit(X, y) clf.predict(X[:5])
多类别和多标签拟合
在多类别拟合的情况下,学习和预测任务都取决于所拟合目标数据的格式。使用的模块是sklearn.multiclass。请查看下面的示例,其中多类别分类器拟合在一维数组上。
示例
from sklearn.svm import SVC from sklearn.multiclass import OneVsRestClassifier from sklearn.preprocessing import LabelBinarizer X = [[1, 2], [3, 4], [4, 5], [5, 2], [1, 1]] y = [0, 0, 1, 1, 2] classif = OneVsRestClassifier(estimator = SVC(gamma = 'scale',random_state = 0)) classif.fit(X, y).predict(X)
输出
array([0, 0, 1, 1, 2])
在上面的例子中,分类器拟合在多类别标签的一维数组上,因此predict()方法提供了相应的多类别预测。但另一方面,也可以拟合在二维的二元标签指示器数组上,如下所示:
示例
from sklearn.svm import SVC from sklearn.multiclass import OneVsRestClassifier from sklearn.preprocessing import LabelBinarizer X = [[1, 2], [3, 4], [4, 5], [5, 2], [1, 1]] y = LabelBinarizer().fit_transform(y) classif.fit(X, y).predict(X)
输出
array(
[
[0, 0, 0],
[0, 0, 0],
[0, 1, 0],
[0, 1, 0],
[0, 0, 0]
]
)
类似地,在多标签拟合的情况下,一个实例可以被赋予多个标签,如下所示:
示例
from sklearn.preprocessing import MultiLabelBinarizer y = [[0, 1], [0, 2], [1, 3], [0, 2, 3], [2, 4]] y = MultiLabelBinarizer().fit_transform(y) classif.fit(X, y).predict(X)
输出
array(
[
[1, 0, 1, 0, 0],
[1, 0, 1, 0, 0],
[1, 0, 1, 1, 0],
[1, 0, 1, 1, 0],
[1, 0, 1, 0, 0]
]
)
在上面的示例中,sklearn.MultiLabelBinarizer用于将多标签的二维数组二值化以进行拟合。这就是为什么predict()函数输出一个二维数组,其中每个实例都有多个标签。
Scikit Learn - 线性模型
本章将帮助您学习Scikit-Learn中的线性建模。让我们首先了解Sklearn中的线性回归是什么。
下表列出了Scikit-Learn提供的各种线性模型:
| 序号 | 模型和描述 |
|---|---|
| 1 |
这是最好的统计模型之一,它研究因变量(Y)与给定的一组自变量(X)之间的关系。 |
| 2 |
逻辑回归,尽管其名称如此,但它是一种分类算法,而不是回归算法。基于给定的一组自变量,它用于估计离散值(0或1,是/否,真/假)。 |
| 3 |
岭回归或Tikhonov正则化是一种正则化技术,它执行L2正则化。它通过添加等于系数大小平方的惩罚(收缩量)来修改损失函数。 |
| 4 |
贝叶斯回归允许使用概率分布器而不是点估计来制定线性回归,从而提供了一种自然的机制来应对数据不足或数据分布不佳的情况。 |
| 5 |
LASSO是一种执行L1正则化的正则化技术。它通过添加等于系数绝对值之和的惩罚(收缩量)来修改损失函数。 |
| 6 |
它允许联合拟合多个回归问题,强制所有回归问题(也称为任务)的选择特征相同。Sklearn提供了一个名为MultiTaskLasso的线性模型,它使用混合L1、L2范数进行正则化训练,从而联合估计多个回归问题的稀疏系数。 |
| 7 |
弹性网络是一种正则化回归方法,它线性组合LASSO和岭回归方法的两种惩罚,即L1和L2。当存在多个相关特征时,它非常有用。 |
| 8 |
这是一个弹性网络模型,允许联合拟合多个回归问题,强制所有回归问题(也称为任务)的选择特征相同。 |
Scikit Learn - 扩展线性模型
本章重点介绍Sklearn中的多项式特征和管道工具。
多项式特征介绍
在数据的非线性函数上训练的线性模型通常保持线性方法的快速性能。它还允许它们拟合更广泛的数据范围。这就是为什么在机器学习中使用这种在非线性函数上训练的线性模型的原因。
一个例子是,可以通过从系数构造多项式特征来扩展简单的线性回归。
数学上,假设我们有标准线性回归模型,那么对于二维数据,它看起来像这样:
$$Y=W_{0}+W_{1}X_{1}+W_{2}X_{2}$$现在,我们可以将特征组合在二阶多项式中,我们的模型将如下所示:
$$Y=W_{0}+W_{1}X_{1}+W_{2}X_{2}+W_{3}X_{1}X_{2}+W_{4}X_1^2+W_{5}X_2^2$$上面仍然是一个线性模型。在这里,我们看到由此产生的多项式回归属于线性模型的同一类,并且可以类似地求解。
为此,scikit-learn提供了一个名为PolynomialFeatures的模块。此模块将输入数据矩阵转换为给定次数的新数据矩阵。
参数
下表包含PolynomialFeatures模块使用的参数
| 序号 | 参数和描述 |
|---|---|
| 1 |
degree − 整数,默认值 = 2 它表示多项式特征的次数。 |
| 2 |
interaction_only − 布尔值,默认值 = false 默认情况下,它是false,但如果设置为true,则会生成大多数次数不同的输入特征的乘积特征。这些特征称为交互特征。 |
| 3 |
include_bias − 布尔值,默认值 = true 它包括一个偏差列,即所有多项式幂都为零的特征。 |
| 4 |
order − str in {‘C’, ‘F’},默认值 = ‘C’ 此参数表示密集情况下输出数组的顺序。’F’顺序意味着计算速度更快,但另一方面,它可能会减慢后续估计器的速度。 |
属性
下表包含PolynomialFeatures模块使用的属性
| 序号 | 属性和描述 |
|---|---|
| 1 |
powers_ − 数组,形状 (n_output_features, n_input_features) 它显示powers_[i,j]是第i个输出中第j个输入的指数。 |
| 2 |
n_input_features_ − int 顾名思义,它给出输入特征的总数。 |
| 3 |
n_output_features_ − int 顾名思义,它给出多项式输出特征的总数。 |
实现示例
下面的Python脚本使用PolynomialFeatures转换器将8的数组转换为形状(4,2):
from sklearn.preprocessing import PolynomialFeatures import numpy as np Y = np.arange(8).reshape(4, 2) poly = PolynomialFeatures(degree=2) poly.fit_transform(Y)
输出
array(
[
[ 1., 0., 1., 0., 0., 1.],
[ 1., 2., 3., 4., 6., 9.],
[ 1., 4., 5., 16., 20., 25.],
[ 1., 6., 7., 36., 42., 49.]
]
)
使用管道工具简化流程
上述预处理,即,将输入数据矩阵转换为给定次数的新数据矩阵,可以使用Pipeline工具简化,这些工具基本上用于将多个估计器链接到一个。
示例
下面的python脚本使用Scikit-learn的管道工具来简化预处理(将拟合到三阶多项式数据)。
#First, import the necessary packages.
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
import numpy as np
#Next, create an object of Pipeline tool
Stream_model = Pipeline([('poly', PolynomialFeatures(degree=3)), ('linear', LinearRegression(fit_intercept=False))])
#Provide the size of array and order of polynomial data to fit the model.
x = np.arange(5)
y = 3 - 2 * x + x ** 2 - x ** 3
Stream_model = model.fit(x[:, np.newaxis], y)
#Calculate the input polynomial coefficients.
Stream_model.named_steps['linear'].coef_
输出
array([ 3., -2., 1., -1.])
上面的输出显示,在多项式特征上训练的线性模型能够恢复精确的输入多项式系数。
Scikit Learn - 随机梯度下降
在这里,我们将学习Sklearn中的一种优化算法,称为随机梯度下降 (SGD)。
随机梯度下降 (SGD) 是一种简单而有效的优化算法,用于查找函数的参数/系数的值,以最小化成本函数。换句话说,它用于在凸损失函数(例如 SVM 和逻辑回归)下进行线性分类器的判别学习。它已成功应用于大规模数据集,因为对系数的更新是在每个训练实例中执行的,而不是在实例结束时执行。
SGD 分类器
随机梯度下降 (SGD) 分类器基本上实现了一个简单的 SGD 学习例程,支持各种用于分类的损失函数和惩罚。Scikit-learn 提供SGDClassifier模块来实现 SGD 分类。
参数
下表包含SGDClassifier模块使用的参数:
| 序号 | 参数和描述 |
|---|---|
| 1 |
loss − str,默认值 = ‘hinge’ 它表示实现时要使用的损失函数。默认值为“hinge”,这将给我们一个线性 SVM。可以使用的其他选项包括:
|
| 2 |
penalty − str,‘none’,‘l2’,‘l1’,‘elasticnet’ 它是模型中使用的正则化项。默认情况下,它是 L2。我们也可以使用 L1 或“elasticnet;但两者都可能使模型稀疏,因此无法使用 L2 实现。 |
| 3 |
alpha − float,默认值 = 0.0001 Alpha,乘以正则化项的常数,是一个调整参数,它决定我们想要惩罚模型的程度。默认值为 0.0001。 |
| 4 |
l1_ratio − float,默认值 = 0.15 这称为 ElasticNet 混合参数。其范围为 0 <= l1_ratio <= 1。如果 l1_ratio = 1,则惩罚将是 L1 惩罚。如果 l1_ratio = 0,则惩罚将是 L2 惩罚。 |
| 5 |
fit_intercept − 布尔值,默认值 = True 此参数指定应向决策函数添加常数(偏差或截距)。如果将其设置为 false,则计算中不会使用截距,并且将假设数据已居中。 |
| 6 |
tol − float 或 none,可选,默认值 = 1.e-3 此参数表示迭代的停止条件。其默认值为 False,但如果设置为 None,则当 𝒍loss > best_loss - tol 连续 n_iter_no_change 个时期时,迭代将停止。 |
| 7 |
shuffle − 布尔值,可选,默认值 = True 此参数表示我们是否希望在每个时期之后对训练数据进行洗牌。 |
| 8 |
verbose − 整数,默认值 = 0 它表示详细程度。其默认值为 0。 |
| 9 |
epsilon − float,默认值 = 0.1 此参数指定不敏感区域的宽度。如果 loss = ‘epsilon-insensitive’,则当前预测与正确标签之间的任何差异小于阈值都将被忽略。 |
| 10 |
max_iter − int,可选,默认值 = 1000 顾名思义,它表示对时期(即训练数据)的最大迭代次数。 |
| 11 |
warm_start − bool,可选,默认值 = false 将此参数设置为 True,我们可以重用对 fit 的先前调用的解决方案作为初始化。如果我们选择默认值 false,它将擦除以前的解决方案。 |
| 12 |
random_state − int,RandomState 实例或 None,可选,默认值 = none 此参数表示用于对数据进行洗牌的伪随机数生成的种子。以下是选项:
|
| 13 |
n_jobs − int 或 none,可选,默认值 = None 它表示用于多类别问题的 OVA(一对多)计算的 CPU 数量。默认值为 none,这意味着 1。 |
| 14 |
learning_rate − string,可选,默认值 = ‘optimal’
|
| 15 |
eta0 − double,默认值 = 0.0 它表示上述学习率选项(即“constant”、“invscalling”或“adaptive”)的初始学习率。 |
| 16 |
power_t − idouble,默认值 =0.5 它是“incscalling”学习率的指数。 |
| 17 |
early_stopping − bool,默认值 = False 此参数表示是否使用提前停止策略,当验证分数不再提高时终止训练。其默认值为false,但当设置为true时,它会自动将训练数据的一部分(分层抽样)作为验证集,并在验证分数不再提高时停止训练。 |
| 18 |
validation_fraction − 浮点数,默认值 = 0.1 仅在early_stopping为true时使用。它表示用于提前停止训练而预留的验证集所占训练数据的比例。 |
| 19 |
n_iter_no_change − 整数,默认值=5 它表示算法在提前停止前允许运行多少次迭代而不改进。 |
| 20 |
class_weight − 字典,{class_label: weight} 或 “balanced”,或 None,可选 此参数表示与各类别相关的权重。如果没有提供,则假定所有类别的权重为1。 |
| 20 |
warm_start − bool,可选,默认值 = false 将此参数设置为 True,我们可以重用对 fit 的先前调用的解决方案作为初始化。如果我们选择默认值 false,它将擦除以前的解决方案。 |
| 21 |
average − 布尔值或整数,可选,默认值 = false 它表示用于多类别问题的 OVA(一对多)计算的 CPU 数量。默认值为 none,这意味着 1。 |
属性
下表列出了SGDClassifier模块使用的属性 −
| 序号 | 属性和描述 |
|---|---|
| 1 |
coef_ − 数组,形状为(1, n_features)(如果n_classes==2),否则为(n_classes, n_features) 此属性提供了分配给特征的权重。 |
| 2 |
intercept_ − 数组,形状为(1,)(如果n_classes==2),否则为(n_classes,) 它表示决策函数中的常数项。 |
| 3 |
n_iter_ − 整数 它给出达到停止准则所需的迭代次数。 |
实现示例
与其他分类器一样,随机梯度下降 (SGD) 必须使用以下两个数组进行拟合 −
一个名为X的数组,包含训练样本。其大小为[n_samples, n_features]。
一个名为Y的数组,包含目标值,即训练样本的类别标签。其大小为[n_samples]。
示例
下面的Python脚本使用SGDClassifier线性模型 −
import numpy as np from sklearn import linear_model X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]]) Y = np.array([1, 1, 2, 2]) SGDClf = linear_model.SGDClassifier(max_iter = 1000, tol=1e-3,penalty = "elasticnet") SGDClf.fit(X, Y)
输出
SGDClassifier( alpha = 0.0001, average = False, class_weight = None, early_stopping = False, epsilon = 0.1, eta0 = 0.0, fit_intercept = True, l1_ratio = 0.15, learning_rate = 'optimal', loss = 'hinge', max_iter = 1000, n_iter = None, n_iter_no_change = 5, n_jobs = None, penalty = 'elasticnet', power_t = 0.5, random_state = None, shuffle = True, tol = 0.001, validation_fraction = 0.1, verbose = 0, warm_start = False )
示例
现在,拟合完成后,模型可以预测新值,如下所示 −
SGDClf.predict([[2.,2.]])
输出
array([2])
示例
对于上述示例,我们可以使用以下Python脚本获取权重向量 −
SGDClf.coef_
输出
array([[19.54811198, 9.77200712]])
示例
同样,我们可以使用以下Python脚本获取截距值 −
SGDClf.intercept_
输出
array([10.])
示例
我们可以使用SGDClassifier.decision_function获取到超平面的带符号距离,如下面的Python脚本所示 −
SGDClf.decision_function([[2., 2.]])
输出
array([68.6402382])
SGD回归器
随机梯度下降 (SGD) 回归器基本上实现了一个简单的SGD学习程序,支持各种损失函数和惩罚项以拟合线性回归模型。Scikit-learn 提供SGDRegressor模块来实现SGD回归。
参数
SGDRegressor使用的参数与SGDClassifier模块中使用的参数几乎相同。区别在于“loss”参数。对于SGDRegressor模块的loss参数,其有效值为:
squared_loss − 指的是普通最小二乘拟合。
huber: SGDRegressor − 通过在超过epsilon距离后从平方损失切换到线性损失来纠正异常值。“huber”的作用是修改“squared_loss”,以便算法更少地关注纠正异常值。
epsilon_insensitive − 实际上,它忽略小于epsilon的误差。
squared_epsilon_insensitive − 与epsilon_insensitive相同。唯一的区别在于,它在超过epsilon的容差后变为平方损失。
另一个区别是名为“power_t”的参数的默认值为0.25,而不是SGDClassifier中的0.5。此外,它没有“class_weight”和“n_jobs”参数。
属性
SGDRegressor的属性也与SGDClassifier模块的属性相同。它另外还有三个属性:
average_coef_ − 数组,形状为(n_features,)
顾名思义,它提供了分配给特征的平均权重。
average_intercept_ − 数组,形状为(1,)
顾名思义,它提供了平均截距项。
t_ − 整数
它提供了在训练阶段执行的权重更新次数。
注意 − average_coef_ 和 average_intercept_ 属性只有在将‘average’参数设置为True后才能使用。
实现示例
下面的Python脚本使用SGDRegressor线性模型 −
import numpy as np from sklearn import linear_model n_samples, n_features = 10, 5 rng = np.random.RandomState(0) y = rng.randn(n_samples) X = rng.randn(n_samples, n_features) SGDReg =linear_model.SGDRegressor( max_iter = 1000,penalty = "elasticnet",loss = 'huber',tol = 1e-3, average = True ) SGDReg.fit(X, y)
输出
SGDRegressor( alpha = 0.0001, average = True, early_stopping = False, epsilon = 0.1, eta0 = 0.01, fit_intercept = True, l1_ratio = 0.15, learning_rate = 'invscaling', loss = 'huber', max_iter = 1000, n_iter = None, n_iter_no_change = 5, penalty = 'elasticnet', power_t = 0.25, random_state = None, shuffle = True, tol = 0.001, validation_fraction = 0.1, verbose = 0, warm_start = False )
示例
现在,拟合完成后,我们可以使用以下Python脚本获取权重向量 −
SGDReg.coef_
输出
array([-0.00423314, 0.00362922, -0.00380136, 0.00585455, 0.00396787])
示例
同样,我们可以使用以下Python脚本获取截距值 −
SGReg.intercept_
输出
SGReg.intercept_
示例
我们可以使用以下Python脚本获取训练阶段的权重更新次数 −
SGDReg.t_
输出
61.0
SGD的优缺点
以下是SGD的优点 −
随机梯度下降 (SGD) 非常高效。
它非常易于实现,因为有很多代码调整的机会。
以下是SGD的缺点 −
随机梯度下降 (SGD) 需要多个超参数,例如正则化参数。
它对特征缩放敏感。
Scikit Learn - 支持向量机
本章介绍一种称为支持向量机 (SVM) 的机器学习方法。
简介
支持向量机 (SVM) 是一种功能强大且灵活的有监督机器学习方法,用于分类、回归和异常值检测。SVM 在高维空间中非常高效,通常用于分类问题。SVM 流行且内存效率高,因为它们在决策函数中只使用训练点的一个子集。
SVM 的主要目标是将数据集划分成多个类别,以便找到一个最大间隔超平面 (MMH),这可以通过以下两个步骤完成 −
支持向量机将首先迭代生成超平面,以最佳方式分离类别。
之后,它将选择能够正确分离类别的超平面。
SVM 中的一些重要概念如下 −
支持向量 − 可以定义为最接近超平面的数据点。支持向量有助于确定分离线。
超平面 − 分隔具有不同类别的对象集的决策平面或空间。
间隔 − 不同类别最接近数据点之间的两条线之间的间隙称为间隔。
下图将使您深入了解这些 SVM 概念 −
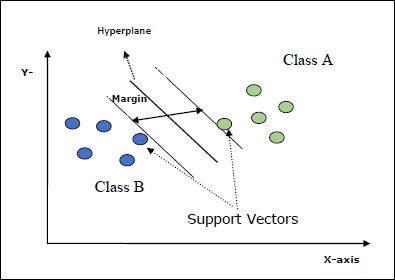
Scikit-learn 中的 SVM 支持稀疏和密集样本向量作为输入。
SVM 分类
Scikit-learn 提供了三个类,即SVC、NuSVC和LinearSVC,它们可以执行多类分类。
SVC
它是C-支持向量分类,其实现基于libsvm。scikit-learn 使用的模块是sklearn.svm.SVC。此类根据一对一方案处理多类支持。
参数
下表列出了sklearn.svm.SVC类使用的参数 −
| 序号 | 参数和描述 |
|---|---|
| 1 |
C − 浮点数,可选,默认值 = 1.0 它是误差项的惩罚参数。 |
| 2 |
kernel − 字符串,可选,默认值 = ‘rbf’ 此参数指定要在算法中使用的内核类型。我们可以从‘linear’、‘poly’、‘rbf’、‘sigmoid’、‘precomputed’中选择一个。内核的默认值为‘rbf’。 |
| 3 |
degree − 整数,可选,默认值 = 3 它表示“poly”内核函数的度数,其他内核将忽略它。 |
| 4 |
gamma − {‘scale’、‘auto’} 或浮点数, 它是内核“rbf”、“poly”和“sigmoid”的内核系数。 |
| 5 |
可选默认值 − = ‘scale’ 如果选择默认值,即 gamma = ‘scale’,则SVC 使用的 gamma 值为 1/(𝑛_𝑓𝑒𝑎𝑡𝑢𝑟𝑒𝑠∗𝑋.𝑣𝑎𝑟())。 另一方面,如果 gamma = ‘auto’,它使用 1/𝑛_𝑓𝑒𝑎𝑡𝑢𝑟𝑒𝑠。 |
| 6 |
coef0 − 浮点数,可选,默认值=0.0 内核函数中的常数项,仅在“poly”和“sigmoid”中有效。 |
| 7 |
tol − 浮点数,可选,默认值 = 1.e-3 此参数表示迭代的停止准则。 |
| 8 |
shrinking − 布尔值,可选,默认值 = True 此参数表示是否要使用收缩启发式。 |
| 9 |
verbose − 布尔值,默认值:false 启用或禁用详细输出。其默认值为false。 |
| 10 |
probability − 布尔值,可选,默认值 = false 此参数启用或禁用概率估计。默认值为false,但在调用fit之前必须启用它。 |
| 11 |
max_iter − 整数,可选,默认值 = -1 顾名思义,它表示求解器中的最大迭代次数。值为-1表示迭代次数没有限制。 |
| 12 |
cache_size − 浮点数,可选 此参数将指定内核缓存的大小。值为MB(兆字节)。 |
| 13 |
random_state − int,RandomState 实例或 None,可选,默认值 = none 此参数表示生成的伪随机数的种子,该种子在洗牌数据时使用。选项如下:
|
| 14 |
class_weight − {字典、‘balanced’},可选 此参数将SVC的第j类的参数C设置为𝑐𝑙𝑎𝑠𝑠_𝑤𝑒𝑖𝑔ℎ𝑡[𝑗]∗𝐶。如果使用默认选项,则表示所有类别的权重都为1。另一方面,如果选择class_weight:balanced,它将使用y的值来自动调整权重。 |
| 15 |
decision_function_shape − ‘ovo’、‘ovr’,默认值 = ‘ovr’ 此参数将决定算法是否返回与所有其他分类器形状相同的‘ovr’(一对多)决策函数,还是libsvm的原始ovo(一对一)决策函数。 |
| 16 |
break_ties − 布尔值,可选,默认值 = false True − predict 将根据 decision_function 的置信度值打破平局 False − predict 将返回平局类别中的第一个类别。 |
属性
下表列出了sklearn.svm.SVC类使用的属性 −
| 序号 | 属性和描述 |
|---|---|
| 1 |
support_ − 类数组,形状 = [n_SV] 它返回支持向量的索引。 |
| 2 |
support_vectors_ − 类数组,形状 = [n_SV, n_features] 它返回支持向量。 |
| 3 |
n_support_ − 类数组,dtype=int32,形状 = [n_class] 它表示每个类别的支持向量数量。 |
| 4 |
dual_coef_ − 数组,形状 = [n_class-1,n_SV] 这些是决策函数中支持向量的系数。 |
| 5 |
coef_ − 数组,形状 = [n_class * (n_class-1)/2, n_features] 此属性仅在线性内核情况下可用,它提供了分配给特征的权重。 |
| 6 |
intercept_ − 数组,形状 = [n_class * (n_class-1)/2] 它表示决策函数中的常数项。 |
| 7 |
fit_status_ − 整数 如果正确拟合,输出将为0。如果错误拟合,输出将为1。 |
| 8 |
classes_ − 形状为[n_classes]的数组 它给出类别的标签。 |
实现示例
与其他分类器一样,SVC 也必须使用以下两个数组进行拟合 −
一个名为X的数组,包含训练样本。其大小为[n_samples, n_features]。
一个名为Y的数组,包含目标值,即训练样本的类别标签。其大小为[n_samples]。
下面的Python脚本使用sklearn.svm.SVC类 −
import numpy as np X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]]) y = np.array([1, 1, 2, 2]) from sklearn.svm import SVC SVCClf = SVC(kernel = 'linear',gamma = 'scale', shrinking = False,) SVCClf.fit(X, y)
输出
SVC(C = 1.0, cache_size = 200, class_weight = None, coef0 = 0.0, decision_function_shape = 'ovr', degree = 3, gamma = 'scale', kernel = 'linear', max_iter = -1, probability = False, random_state = None, shrinking = False, tol = 0.001, verbose = False)
示例
现在,拟合完成后,我们可以使用以下Python脚本获取权重向量 −
SVCClf.coef_
输出
array([[0.5, 0.5]])
示例
同样,我们可以获取其他属性的值,如下所示 −
SVCClf.predict([[-0.5,-0.8]])
输出
array([1])
示例
SVCClf.n_support_
输出
array([1, 1])
示例
SVCClf.support_vectors_
输出
array(
[
[-1., -1.],
[ 1., 1.]
]
)
示例
SVCClf.support_
输出
array([0, 2])
示例
SVCClf.intercept_
输出
array([-0.])
示例
SVCClf.fit_status_
输出
0
NuSVC
NuSVC 是 Nu 支持向量分类。它是scikit-learn提供的另一个可以执行多类分类的类。它类似于SVC,但NuSVC接受略微不同的参数集。与SVC不同的参数如下:
nu − 浮点数,可选,默认值 = 0.5
它表示训练错误比例的上限和支持向量比例的下限。其值应在 (0,1] 区间内。
其余参数和属性与 SVC 相同。
实现示例
我们也可以使用sklearn.svm.NuSVC类实现相同的示例。
import numpy as np X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]]) y = np.array([1, 1, 2, 2]) from sklearn.svm import NuSVC NuSVCClf = NuSVC(kernel = 'linear',gamma = 'scale', shrinking = False,) NuSVCClf.fit(X, y)
输出
NuSVC(cache_size = 200, class_weight = None, coef0 = 0.0, decision_function_shape = 'ovr', degree = 3, gamma = 'scale', kernel = 'linear', max_iter = -1, nu = 0.5, probability = False, random_state = None, shrinking = False, tol = 0.001, verbose = False)
我们可以像 SVC 那样获取其余属性的输出。
LinearSVC
它是线性支持向量分类器。它类似于具有 kernel = 'linear' 的 SVC。它们的区别在于LinearSVC基于liblinear实现,而SVC基于libsvm实现。这就是LinearSVC在惩罚项和损失函数的选择上具有更大灵活性的原因。它也更能适应大量的样本。
如果我们谈论它的参数和属性,它不支持'kernel',因为它被假定为线性,并且它也缺少一些属性,例如support_,support_vectors_,n_support_,fit_status_和dual_coef_。
但是,它支持penalty和loss参数,如下所示:
penalty − 字符串,L1 或 L2(默认 = 'L2')
此参数用于指定惩罚(正则化)中使用的范数(L1 或 L2)。
loss − 字符串,hinge,squared_hinge(默认 = squared_hinge)
它表示损失函数,其中 'hinge' 是标准 SVM 损失,'squared_hinge' 是 hinge 损失的平方。
实现示例
以下 Python 脚本使用sklearn.svm.LinearSVC类:
from sklearn.svm import LinearSVC from sklearn.datasets import make_classification X, y = make_classification(n_features = 4, random_state = 0) LSVCClf = LinearSVC(dual = False, random_state = 0, penalty = 'l1',tol = 1e-5) LSVCClf.fit(X, y)
输出
LinearSVC(C = 1.0, class_weight = None, dual = False, fit_intercept = True, intercept_scaling = 1, loss = 'squared_hinge', max_iter = 1000, multi_class = 'ovr', penalty = 'l1', random_state = 0, tol = 1e-05, verbose = 0)
示例
现在,拟合完成后,模型可以预测新值,如下所示 −
LSVCClf.predict([[0,0,0,0]])
输出
[1]
示例
对于上述示例,我们可以使用以下Python脚本获取权重向量 −
LSVCClf.coef_
输出
[[0. 0. 0.91214955 0.22630686]]
示例
同样,我们可以使用以下Python脚本获取截距值 −
LSVCClf.intercept_
输出
[0.26860518]
SVM 回归
如前所述,SVM 用于分类和回归问题。Scikit-learn 的支持向量分类 (SVC) 方法也可以扩展到解决回归问题。这种扩展的方法称为支持向量回归 (SVR)。
SVM 和 SVR 的基本相似性
SVC 创建的模型仅依赖于训练数据的一个子集。为什么?因为构建模型的成本函数并不关心位于边界之外的训练数据点。
而 SVR(支持向量回归)生成的模型也仅依赖于训练数据的一个子集。为什么?因为构建模型的成本函数忽略了任何接近模型预测的训练数据点。
Scikit-learn 提供三个类,即SVR、NuSVR 和 LinearSVR,作为 SVR 的三种不同实现。
SVR
它是 Epsilon-支持向量回归,其实现基于libsvm。与SVC相反,模型中有两个自由参数,即'C'和'epsilon'。
epsilon − 浮点数,可选,默认 = 0.1
它表示 epsilon-SVR 模型中的 epsilon,并指定 epsilon 管,在该管内,训练损失函数中与预测值与实际值距离在 epsilon 之内的点没有关联的惩罚。
其余参数和属性与我们在SVC中使用的相似。
实现示例
以下 Python 脚本使用sklearn.svm.SVR类:
from sklearn import svm X = [[1, 1], [2, 2]] y = [1, 2] SVRReg = svm.SVR(kernel = ’linear’, gamma = ’auto’) SVRReg.fit(X, y)
输出
SVR(C = 1.0, cache_size = 200, coef0 = 0.0, degree = 3, epsilon = 0.1, gamma = 'auto', kernel = 'linear', max_iter = -1, shrinking = True, tol = 0.001, verbose = False)
示例
现在,拟合完成后,我们可以使用以下Python脚本获取权重向量 −
SVRReg.coef_
输出
array([[0.4, 0.4]])
示例
同样,我们可以获取其他属性的值,如下所示 −
SVRReg.predict([[1,1]])
输出
array([1.1])
同样,我们也可以获取其他属性的值。
NuSVR
NuSVR 是 Nu 支持向量回归。它类似于 NuSVC,但 NuSVR 使用参数nu来控制支持向量的数量。此外,与 NuSVC 中nu替换 C 参数不同,这里它替换了epsilon。
实现示例
以下 Python 脚本使用sklearn.svm.SVR类:
from sklearn.svm import NuSVR import numpy as np n_samples, n_features = 20, 15 np.random.seed(0) y = np.random.randn(n_samples) X = np.random.randn(n_samples, n_features) NuSVRReg = NuSVR(kernel = 'linear', gamma = 'auto',C = 1.0, nu = 0.1)^M NuSVRReg.fit(X, y)
输出
NuSVR(C = 1.0, cache_size = 200, coef0 = 0.0, degree = 3, gamma = 'auto', kernel = 'linear', max_iter = -1, nu = 0.1, shrinking = True, tol = 0.001, verbose = False)
示例
现在,拟合完成后,我们可以使用以下Python脚本获取权重向量 −
NuSVRReg.coef_
输出
array(
[
[-0.14904483, 0.04596145, 0.22605216, -0.08125403, 0.06564533,
0.01104285, 0.04068767, 0.2918337 , -0.13473211, 0.36006765,
-0.2185713 , -0.31836476, -0.03048429, 0.16102126, -0.29317051]
]
)
同样,我们也可以获取其他属性的值。
LinearSVR
它是线性支持向量回归。它类似于具有 kernel = 'linear' 的 SVR。它们的区别在于LinearSVR基于liblinear实现,而SVC基于libsvm实现。这就是LinearSVR在惩罚项和损失函数的选择上具有更大灵活性的原因。它也更能适应大量的样本。
如果我们谈论它的参数和属性,它不支持'kernel',因为它被假定为线性,并且它也缺少一些属性,例如support_,support_vectors_,n_support_,fit_status_和dual_coef_。
但是,它支持如下所示的 'loss' 参数:
loss − 字符串,可选,默认 = 'epsilon_insensitive'
它表示损失函数,其中 epsilon_insensitive 损失是 L1 损失,平方 epsilon_insensitive 损失是 L2 损失。
实现示例
以下 Python 脚本使用sklearn.svm.LinearSVR类:
from sklearn.svm import LinearSVR from sklearn.datasets import make_regression X, y = make_regression(n_features = 4, random_state = 0) LSVRReg = LinearSVR(dual = False, random_state = 0, loss = 'squared_epsilon_insensitive',tol = 1e-5) LSVRReg.fit(X, y)
输出
LinearSVR( C=1.0, dual=False, epsilon=0.0, fit_intercept=True, intercept_scaling=1.0, loss='squared_epsilon_insensitive', max_iter=1000, random_state=0, tol=1e-05, verbose=0 )
示例
现在,拟合完成后,模型可以预测新值,如下所示 −
LSRReg.predict([[0,0,0,0]])
输出
array([-0.01041416])
示例
对于上述示例,我们可以使用以下Python脚本获取权重向量 −
LSRReg.coef_
输出
array([20.47354746, 34.08619401, 67.23189022, 87.47017787])
示例
同样,我们可以使用以下Python脚本获取截距值 −
LSRReg.intercept_
输出
array([-0.01041416])
Scikit Learn - 异常检测
在这里,我们将学习什么是 Sklearn 中的异常检测以及它如何用于识别数据点。
异常检测是一种用于识别数据集中与其余数据不匹配的数据点的技术。它在商业中有很多应用,例如欺诈检测、入侵检测、系统健康监控、监控和预测性维护。异常(也称为异常值)可以分为以下三类:
点异常− 当单个数据实例相对于其余数据被认为是异常时发生。
上下文异常− 此类异常是特定于上下文的。如果数据实例在特定上下文中是异常的,则会发生这种情况。
集体异常− 当一组相关的数据实例相对于整个数据集而不是单个值是异常时发生。
方法
可以使用两种方法,即异常值检测和新颖性检测,进行异常检测。有必要了解它们之间的区别。
异常值检测
训练数据包含远离其余数据的异常值。此类异常值定义为观察值。这就是为什么异常值检测估计器总是试图拟合具有最集中训练数据的区域,同时忽略异常观察值的原因。它也称为无监督异常检测。
新颖性检测
它关注的是检测训练数据中未包含的新观测值中的未观察到的模式。这里,训练数据没有被异常值污染。它也称为半监督异常检测。
scikit-learn 提供了一组 ML 工具,可用于异常值检测和新颖性检测。这些工具首先通过使用 fit() 方法无监督地从数据中实现对象学习,如下所示:
estimator.fit(X_train)
现在,新的观察结果将使用 predict() 方法分类为内点 (标记为 1) 或异常点 (标记为 -1),如下所示:
estimator.fit(X_test)
估计器将首先计算原始评分函数,然后预测方法将对该原始评分函数使用阈值。我们可以借助score_sample方法访问此原始评分函数,并可以通过contamination参数控制阈值。
我们还可以定义decision_function方法,该方法将异常值定义为负值,将内点定义为非负值。
estimator.decision_function(X_test)
Sklearn 的异常值检测算法
让我们首先了解什么是椭圆包络。
拟合椭圆包络
该算法假设常规数据来自已知分布,例如高斯分布。对于异常值检测,Scikit-learn 提供了一个名为covariance.EllipticEnvelop的对象。
此对象将稳健的协方差估计拟合到数据,从而将椭圆拟合到中心数据点。它忽略中心模式之外的点。
参数
下表包含sklearn.covariance.EllipticEnvelop方法使用的参数:
| 序号 | 参数和描述 |
|---|---|
| 1 |
store_precision − 布尔值,可选,默认 = True 如果存储估计的精度,我们可以指定它。 |
| 2 |
assume_centered − 布尔值,可选,默认 = False 如果我们将其设置为 False,它将使用 FastMCD 算法直接计算稳健的位置和协方差。另一方面,如果设置为 True,它将计算稳健位置和协方差的支持。 |
| 3 |
support_fraction − (0., 1.) 内的浮点数,可选,默认 = None 此参数告诉方法有多少比例的点应包含在原始 MCD 估计的支持中。 |
| 4 |
contamination − (0., 1.) 内的浮点数,可选,默认 = 0.1 它提供了数据集中异常值的比例。 |
| 5 |
random_state − int,RandomState 实例或 None,可选,默认值 = none 此参数表示生成的伪随机数的种子,该种子在洗牌数据时使用。选项如下:
|
属性
下表包含sklearn.covariance.EllipticEnvelop方法使用的属性:
| 序号 | 属性和描述 |
|---|---|
| 1 |
support_ − 类似数组,形状 (n_samples,) 它表示用于计算位置和形状的稳健估计的观察值的掩码。 |
| 2 |
location_ − 类似数组,形状 (n_features) 它返回估计的稳健位置。 |
| 3 |
covariance_ − 类似数组,形状 (n_features, n_features) 它返回估计的稳健协方差矩阵。 |
| 4 |
precision_ − 类似数组,形状 (n_features, n_features) 它返回估计的伪逆矩阵。 |
| 5 |
offset_ − 浮点数 它用于根据原始分数定义决策函数。decision_function = score_samples - offset_ |
实现示例
import numpy as np^M from sklearn.covariance import EllipticEnvelope^M true_cov = np.array([[.5, .6],[.6, .4]]) X = np.random.RandomState(0).multivariate_normal(mean = [0, 0], cov=true_cov,size=500) cov = EllipticEnvelope(random_state = 0).fit(X)^M # Now we can use predict method. It will return 1 for an inlier and -1 for an outlier. cov.predict([[0, 0],[2, 2]])
输出
array([ 1, -1])
隔离森林
对于高维数据集,一种有效的异常值检测方法是使用随机森林。scikit-learn 提供了ensemble.IsolationForest方法,该方法通过随机选择特征来隔离观察值。之后,它会在所选特征的最大值和最小值之间随机选择一个值。
在这里,隔离样本所需的分割次数等于从根节点到终止节点的路径长度。
参数
下表包含sklearn.ensemble.IsolationForest方法使用的参数:
| 序号 | 参数和描述 |
|---|---|
| 1 |
n_estimators − 整数,可选,默认 = 100 它表示集成中基本估计器的数量。 |
| 2 |
max_samples − 整数或浮点数,可选,默认 = “auto” 它表示要从 X 中抽取以训练每个基本估计器的样本数。如果我们选择整数作为其值,它将抽取 max_samples 个样本。如果我们选择浮点数作为其值,它将抽取 max_samples * 𝑋.shape[0] 个样本。并且,如果我们选择 auto 作为其值,它将抽取 max_samples = min(256, n_samples)。 |
| 3 |
support_fraction − (0., 1.) 内的浮点数,可选,默认 = None 此参数告诉方法有多少比例的点应包含在原始 MCD 估计的支持中。 |
| 4 |
contamination − auto 或浮点数,可选,默认 = auto 它提供了数据集中异常值的比例。如果我们将其设置为默认值,即 auto,它将像在原始论文中一样确定阈值。如果设置为浮点数,则污染范围将在 [0,0.5] 范围内。 |
| 5 |
random_state − int,RandomState 实例或 None,可选,默认值 = none 此参数表示生成的伪随机数的种子,该种子在洗牌数据时使用。选项如下:
|
| 6 |
max_features − 整数或浮点数,可选(默认 = 1.0) 它表示要从 X 中抽取以训练每个基本估计器的特征数。如果我们选择整数作为其值,它将抽取 max_features 个特征。如果我们选择浮点数作为其值,它将抽取 max_features * X.shape[1] 个样本。 |
| 7 | bootstrap − 布尔值,可选(默认 = False) 其默认选项为 False,这意味着将不进行替换地进行采样。另一方面,如果设置为 True,则表示单个树拟合训练数据的随机子集,并进行替换采样。 |
| 8 |
n_jobs − 整数或 None,可选(默认 = None) 它表示要为fit()和predict()方法并行运行的作业数。 |
| 9 |
verbose − 整数,可选(默认 = 0) 此参数控制树构建过程的详细程度。 |
| 10 |
warm_start − 布尔值,可选(默认 = False) 如果 warm_start = true,我们可以重复使用之前的调用解决方案来拟合,并且可以向集成中添加更多估计器。但是,如果设置为 false,我们需要拟合一个全新的森林。 |
属性
下表包含sklearn.ensemble.IsolationForest方法使用的属性:
| 序号 | 属性和描述 |
|---|---|
| 1 |
estimators_ − DecisionTreeClassifier 列表 提供所有拟合的子估计器的集合。 |
| 2 |
max_samples_ − 整数 它提供使用的实际样本数。 |
| 3 |
offset_ − 浮点数 它用于根据原始分数定义决策函数。decision_function = score_samples - offset_ |
实现示例
下面的 Python 脚本将使用sklearn.ensemble.IsolationForest方法在给定数据上拟合10棵树。
from sklearn.ensemble import IsolationForest import numpy as np X = np.array([[-1, -2], [-3, -3], [-3, -4], [0, 0], [-50, 60]]) OUTDClf = IsolationForest(n_estimators = 10) OUTDclf.fit(X)
输出
IsolationForest( behaviour = 'old', bootstrap = False, contamination='legacy', max_features = 1.0, max_samples = 'auto', n_estimators = 10, n_jobs=None, random_state = None, verbose = 0 )
局部异常因子
局部异常因子 (LOF) 算法是另一种有效的算法,用于对高维数据执行异常值检测。scikit-learn 提供了neighbors.LocalOutlierFactor 方法,该方法计算一个分数,称为局部异常因子,反映了观测值的异常程度。该算法的主要逻辑是检测密度明显低于其邻居的样本。这就是为什么它根据其邻居来测量给定数据点的局部密度偏差。
参数
下表列出了sklearn.neighbors.LocalOutlierFactor方法使用的参数。
| 序号 | 参数和描述 |
|---|---|
| 1 |
n_neighbors − int,可选,默认为 20 它表示 kneighbors 查询默认使用的邻居数。如果使用点,则将使用所有样本。 |
| 2 |
algorithm − 可选 用于计算最近邻居的算法。
|
| 3 |
leaf_size − int,可选,默认为 30 此参数的值会影响构建和查询的速度。它还会影响存储树所需的内存。此参数传递给 BallTree 或 KdTree 算法。 |
| 4 |
contamination − auto 或浮点数,可选,默认 = auto 它提供了数据集中异常值的比例。如果我们将其设置为默认值,即 auto,它将像在原始论文中一样确定阈值。如果设置为浮点数,则污染范围将在 [0,0.5] 范围内。 |
| 5 |
metric − 字符串或可调用对象,默认值 它表示用于距离计算的度量。 |
| 6 |
P − int,可选(默认为 2) 它是 Minkowski 度量的参数。P=1 等效于使用 manhattan_distance,即 L1,而 P=2 等效于使用 euclidean_distance,即 L2。 |
| 7 |
novelty − 布尔值,(默认为 False) 默认情况下,LOF 算法用于异常值检测,但如果我们将 novelty 设置为 true,则可以将其用于新颖性检测。 |
| 8 |
n_jobs − 整数或 None,可选(默认 = None) 它表示要为 fit() 和 predict() 方法并行运行的作业数。 |
属性
下表列出了sklearn.neighbors.LocalOutlierFactor方法使用的属性。
| 序号 | 属性和描述 |
|---|---|
| 1 |
negative_outlier_factor_ − numpy 数组,形状 (n_samples,) 提供训练样本的相反 LOF。 |
| 2 |
n_neighbors_ − 整数 它提供用于邻居查询的实际邻居数。 |
| 3 |
offset_ − 浮点数 它用于根据原始分数定义二元标签。 |
实现示例
下面给出的 Python 脚本将使用sklearn.neighbors.LocalOutlierFactor方法从任何与我们的数据集对应的数组构建 NeighborsClassifier 类。
from sklearn.neighbors import NearestNeighbors samples = [[0., 0., 0.], [0., .5, 0.], [1., 1., .5]] LOFneigh = NearestNeighbors(n_neighbors = 1, algorithm = "ball_tree",p=1) LOFneigh.fit(samples)
输出
NearestNeighbors( algorithm = 'ball_tree', leaf_size = 30, metric='minkowski', metric_params = None, n_jobs = None, n_neighbors = 1, p = 1, radius = 1.0 )
示例
现在,我们可以使用下面的 Python 脚本,从这个构建的分类器中询问与 [0.5, 1., 1.5] 最接近的点。
print(neigh.kneighbors([[.5, 1., 1.5]])
输出
(array([[1.7]]), array([[1]], dtype = int64))
一类 SVM
由 Schölkopf 等人提出的 One-Class SVM 是一种无监督的异常值检测方法。它在高维数据中也非常有效,并估计高维分布的支持。它在Sklearn.svm.OneClassSVM 对象的支持向量机模块中实现。为了定义边界,它需要一个核(最常用的是 RBF)和一个标量参数。
为了更好地理解,让我们用svm.OneClassSVM对象拟合我们的数据。
示例
from sklearn.svm import OneClassSVM X = [[0], [0.89], [0.90], [0.91], [1]] OSVMclf = OneClassSVM(gamma = 'scale').fit(X)
现在,我们可以按如下方式获取输入数据的 score_samples:
OSVMclf.score_samples(X)
输出
array([1.12218594, 1.58645126, 1.58673086, 1.58645127, 1.55713767])
Scikit Learn - K 近邻 (KNN)
本章将帮助您了解 Sklearn 中的最近邻方法。
基于邻域的学习方法既有监督又有非监督类型。监督的基于邻域的学习可用于分类和回归预测问题,但在工业中主要用于分类预测问题。
基于邻域的学习方法没有专门的训练阶段,并在分类时使用所有数据进行训练。它也不对底层数据做任何假设。这就是它们本质上是懒惰的和非参数的原因。
最近邻方法背后的主要原理是:
找到距离新数据点最近的预定义数量的训练样本。
根据这些训练样本预测标签。
这里,样本数量可以是用户定义的常量(如在 K 近邻学习中),也可以根据点的局部密度而变化(如在基于半径的邻域学习中)。
sklearn.neighbors 模块
Scikit-learn 有sklearn.neighbors模块,它为基于无监督和监督邻域的学习方法提供功能。作为输入,此模块中的类可以处理 NumPy 数组或scipy.sparse矩阵。
算法类型
可在基于邻域的方法的实现中使用的不同类型的算法如下:
暴力搜索
计算数据集中所有点对之间的距离的暴力方法提供了最简单的最近邻搜索实现。从数学上讲,对于 D 维中的 N 个样本,暴力方法的规模为O[DN2]。
对于小的数据样本,此算法非常有用,但是随着样本数量的增加,它变得不可行。可以通过编写关键字algorithm='brute'来启用暴力搜索。
KD 树
为了解决暴力方法的计算效率低下的问题,人们发明了一种基于树的数据结构,即 KD 树数据结构。基本上,KD 树是一种二叉树结构,称为 K 维树。它通过将参数空间沿数据轴递归地划分成嵌套的正交区域来划分参数空间,并将数据点填充到这些区域中。
优点
以下是 KD 树算法的一些优点:
构建速度快 − 由于分区仅沿数据轴进行,因此 KD 树的构建速度非常快。
距离计算少 − 此算法只需要很少的距离计算就能确定查询点的最近邻。它只需要O[log(N)]次距离计算。
缺点
仅对低维邻域搜索速度快 − 它对低维 (D < 20) 邻域搜索速度非常快,但是随着 D 的增长,它变得效率低下。由于分区仅沿数据轴进行,
可以通过编写关键字algorithm='kd_tree'来启用 KD 树邻域搜索。
球树
众所周知,KD 树在更高维度上效率低下,因此,为了解决 KD 树的这种效率低下,开发了球树数据结构。从数学上讲,它将数据递归地划分为由质心 C 和半径 r 定义的节点,使得节点中的每个点都位于由质心C和半径r定义的超球体内。它使用下面给出的三角不等式,减少了最近邻搜索的候选点数
$$ \arrowvert X+Y\arrowvert\leq \arrowvert X\arrowvert+\arrowvert Y\arrowvert $$优点
以下是球树算法的一些优点:
在高度结构化的数据上效率高 − 由于球树将数据划分成一系列嵌套的超球体,因此它在高度结构化的数据上效率很高。
优于 KD 树 − 球树在高维情况下优于 KD 树,因为它具有球树节点的球形几何形状。
缺点
代价高昂 − 将数据划分成一系列嵌套的超球体使其构建代价非常高昂。
可以通过编写关键字algorithm='ball_tree'来启用球树邻域搜索。
选择最近邻算法
为给定数据集选择最佳算法取决于以下因素:
样本数 (N) 和维度 (D)
在选择最近邻算法时,这是最重要的因素。原因如下:
暴力算法的查询时间增长为 O[DN]。
球树算法的查询时间增长为 O[D log(N)]。
KD 树算法的查询时间随 D 的变化方式很奇怪,很难表征。当 D < 20 时,成本为 O[D log(N)],此算法非常有效。另一方面,当 D > 20 时,它效率低下,因为成本增加到接近 O[DN]。
数据结构
影响这些算法性能的另一个因素是数据的内在维度或数据的稀疏性。这是因为球树和 KD 树算法的查询时间会受到它的很大影响。而暴力算法的查询时间不受数据结构的影响。通常,球树和 KD 树算法在应用于具有较小内在维度的稀疏数据时会产生更快的查询时间。
邻居数 (k)
为查询点请求的邻居数 (k) 会影响球树和 KD 树算法的查询时间。随着邻居数 (k) 的增加,它们的查询时间会变慢。而暴力算法的查询时间将不受 k 值的影响。
查询点数
因为它们需要构建阶段,所以如果查询点很多,KD 树和球树算法将非常有效。另一方面,如果查询点较少,则暴力算法的性能优于 KD 树和球树算法。
Scikit Learn - KNN 学习
k-NN (k 近邻) 是最简单的机器学习算法之一,其本质是非参数的和懒惰的。非参数意味着对底层数据分布没有假设,即模型结构由数据集决定。懒惰或基于实例的学习意味着为了生成模型,它不需要任何训练数据点,并且在测试阶段使用所有训练数据。
k-NN 算法包括以下两个步骤:
步骤 1
在此步骤中,它计算并存储训练集中每个样本的 k 个最近邻。
步骤 2
在此步骤中,对于未标记的样本,它从数据集中检索 k 个最近邻。然后,在这些 k 个最近邻中,它通过投票来预测类别(得票最多的类别获胜)。
实现 k 近邻算法的模块sklearn.neighbors为无监督和监督基于邻域的学习方法提供了功能。
无监督最近邻实现不同的算法(BallTree、KDTree 或暴力搜索)来为每个样本找到最近邻。这个无监督版本基本上只是上面讨论的步骤 1,并且是许多算法(KNN 和 K 均值是最著名的)的基础,这些算法需要邻域搜索。简单来说,它是用于实现邻域搜索的无监督学习器。
另一方面,监督的基于邻域的学习用于分类和回归。
无监督 KNN 学习
如上所述,存在许多像 KNN 和 K 均值这样的算法需要最近邻搜索。这就是为什么 Scikit-learn 决定将其邻域搜索部分实现为它自己的“学习器”。将邻域搜索作为单独的学习器的原因是,为了寻找最近邻而计算所有成对距离显然效率不高。让我们看看 Sklearn 用于实现无监督最近邻学习的模块以及示例。
Scikit-learn 模块
sklearn.neighbors.NearestNeighbors 模块用于实现无监督最近邻学习。它使用名为 BallTree、KDTree 或 Brute Force 的特定最近邻算法。换句话说,它充当这三种算法的统一接口。
参数
下表列出了NearestNeighbors 模块使用的参数:
| 序号 | 参数和描述 |
|---|---|
| 1 |
n_neighbors − int,可选 要获取的邻居数量。默认值为 5。 |
| 2 |
radius − float,可选 它限制返回邻居的距离。默认值为 1.0。 |
| 3 |
algorithm − {‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’},可选 此参数将采用您要用于计算最近邻的算法(BallTree、KDTree 或 Brute-force)。如果您提供 'auto',它将尝试根据传递给 fit 方法的值确定最合适的算法。 |
| 4 |
leaf_size − int,可选 它可以影响构建和查询的速度以及存储树所需的内存。它传递给 BallTree 或 KDTree。虽然最佳值取决于问题的性质,但其默认值为 30。 |
| 5 |
metric − 字符串或可调用对象 这是用于计算点之间距离的度量。我们可以将其作为字符串或可调用函数传递。对于可调用函数,度量标准将应用于每一对行,并记录结果值。这不如将度量名称作为字符串传递高效。 我们可以从 scikit-learn 或 scipy.spatial.distance 中选择度量标准。有效值为: Scikit-learn − [‘cosine’,’manhattan’,’Euclidean’, ‘l1’,’l2’, ‘cityblock’] Scipy.spatial.distance − [‘braycurtis’,’canberra’,’chebyshev’,’dice’,’hamming’,’jaccard’, ‘correlation’,’kulsinski’,’mahalanobis’,’minkowski’,’rogerstanimoto’,’russellrao’, ‘sokalmicheme’,’sokalsneath’, ‘seuclidean’, ‘sqeuclidean’, ‘yule’]。 默认度量为 'Minkowski'。 |
| 6 |
P − 整数,可选 它是 Minkowski 度量的参数。默认值为 2,相当于使用 Euclidean_distance(l2)。 |
| 7 |
metric_params − dict,可选 这是度量函数的其他关键字参数。默认值为 None。 |
| 8 |
N_jobs − int 或 None,可选 它表示要为邻居搜索运行的并行作业数。默认值为 None。 |
实现示例
下面的示例将使用sklearn.neighbors.NearestNeighbors 模块查找两组数据之间的最近邻。
首先,我们需要导入所需的模块和包:
from sklearn.neighbors import NearestNeighbors import numpy as np
现在,导入包后,定义我们想要找到最近邻的数据集:
Input_data = np.array([[-1, 1], [-2, 2], [-3, 3], [1, 2], [2, 3], [3, 4],[4, 5]])
接下来,应用无监督学习算法,如下所示:
nrst_neigh = NearestNeighbors(n_neighbors = 3, algorithm = 'ball_tree')
接下来,用输入数据集拟合模型。
nrst_neigh.fit(Input_data)
现在,找到数据集的 K 近邻。它将返回每个点的邻居的索引和距离。
distances, indices = nbrs.kneighbors(Input_data) indices
输出
array(
[
[0, 1, 3],
[1, 2, 0],
[2, 1, 0],
[3, 4, 0],
[4, 5, 3],
[5, 6, 4],
[6, 5, 4]
], dtype = int64
)
distances
输出
array(
[
[0. , 1.41421356, 2.23606798],
[0. , 1.41421356, 1.41421356],
[0. , 1.41421356, 2.82842712],
[0. , 1.41421356, 2.23606798],
[0. , 1.41421356, 1.41421356],
[0. , 1.41421356, 1.41421356],
[0. , 1.41421356, 2.82842712]
]
)
上述输出表明,每个点的最近邻都是该点本身,即为零。这是因为查询集与训练集匹配。
示例
我们还可以通过生成稀疏图来显示相邻点之间的连接,如下所示:
nrst_neigh.kneighbors_graph(Input_data).toarray()
输出
array(
[
[1., 1., 0., 1., 0., 0., 0.],
[1., 1., 1., 0., 0., 0., 0.],
[1., 1., 1., 0., 0., 0., 0.],
[1., 0., 0., 1., 1., 0., 0.],
[0., 0., 0., 1., 1., 1., 0.],
[0., 0., 0., 0., 1., 1., 1.],
[0., 0., 0., 0., 1., 1., 1.]
]
)
一旦我们拟合了无监督NearestNeighbors 模型,数据将存储在基于参数'algorithm'设置的值的数据结构中。之后,我们可以在需要邻居搜索的模型中使用这个无监督学习器的kneighbors。
完整的可运行程序
from sklearn.neighbors import NearestNeighbors import numpy as np Input_data = np.array([[-1, 1], [-2, 2], [-3, 3], [1, 2], [2, 3], [3, 4],[4, 5]]) nrst_neigh = NearestNeighbors(n_neighbors = 3, algorithm='ball_tree') nrst_neigh.fit(Input_data) distances, indices = nbrs.kneighbors(Input_data) indices distances nrst_neigh.kneighbors_graph(Input_data).toarray()
有监督 KNN 学习
有监督的基于邻居的学习用于以下方面:
- 分类,用于具有离散标签的数据
- 回归,用于具有连续标签的数据。
最近邻分类器
我们可以借助以下两个特征来理解基于邻居的分类:
- 它是根据每个点的最近邻的简单多数投票计算的。
- 它只是存储训练数据的实例,因此它是一种非泛化学习。
Scikit-learn 模块
以下是 scikit-learn 使用的两种不同类型的最近邻分类器:
| 序号 | 分类器和描述 |
|---|---|
| 1. | KNeighborsClassifier
分类器名称中的 K 代表 k 个最近邻,其中 k 是用户指定的整数值。因此,顾名思义,此分类器实现了基于 k 个最近邻的学习。k 值的选择取决于数据。 |
| 2. | RadiusNeighborsClassifier
分类器名称中的 Radius 代表指定半径 r 内的最近邻,其中 r 是用户指定的浮点值。因此,顾名思义,此分类器实现了基于每个训练点固定半径 r 内的邻居数量的学习。 |
最近邻回归器
它用于数据标签本质上是连续的情况。分配的数据标签是根据其最近邻的标签的平均值计算的。
以下是 scikit-learn 使用的两种不同类型的最近邻回归器:
KNeighborsRegressor
回归器名称中的 K 代表 k 个最近邻,其中k是用户指定的整数值。因此,顾名思义,此回归器实现了基于 k 个最近邻的学习。k 值的选择取决于数据。让我们通过一个实现示例来更好地理解它。
以下是 scikit-learn 使用的两种不同类型的最近邻回归器:
实现示例
在这个示例中,我们将使用 scikit-learn KNeighborsRegressor 在名为 Iris 花数据集的数据集上实现 KNN。
首先,导入 iris 数据集,如下所示:
from sklearn.datasets import load_iris iris = load_iris()
现在,我们需要将数据分成训练数据和测试数据。我们将使用 Sklearn train_test_split 函数将数据分成 70(训练数据)和 20(测试数据)的比例:
X = iris.data[:, :4] y = iris.target from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20)
接下来,我们将使用 Sklearn 预处理模块进行数据缩放,如下所示:
from sklearn.preprocessing import StandardScaler scaler = StandardScaler() scaler.fit(X_train) X_train = scaler.transform(X_train) X_test = scaler.transform(X_test)
接下来,从 Sklearn 导入KNeighborsRegressor 类,并提供邻居的值,如下所示。
示例
import numpy as np from sklearn.neighbors import KNeighborsRegressor knnr = KNeighborsRegressor(n_neighbors = 8) knnr.fit(X_train, y_train)
输出
KNeighborsRegressor( algorithm = 'auto', leaf_size = 30, metric = 'minkowski', metric_params = None, n_jobs = None, n_neighbors = 8, p = 2, weights = 'uniform' )
示例
现在,我们可以找到 MSE(均方误差),如下所示:
print ("The MSE is:",format(np.power(y-knnr.predict(X),4).mean()))
输出
The MSE is: 4.4333349609375
示例
现在,用它来预测值,如下所示:
X = [[0], [1], [2], [3]] y = [0, 0, 1, 1] from sklearn.neighbors import KNeighborsRegressor knnr = KNeighborsRegressor(n_neighbors = 3) knnr.fit(X, y) print(knnr.predict([[2.5]]))
输出
[0.66666667]
完整的可运行程序
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
import numpy as np
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors=8)
knnr.fit(X_train, y_train)
print ("The MSE is:",format(np.power(y-knnr.predict(X),4).mean()))
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors=3)
knnr.fit(X, y)
print(knnr.predict([[2.5]]))
RadiusNeighborsRegressor
回归器名称中的 Radius 代表指定半径 r 内的最近邻,其中 r 是用户指定的浮点值。因此,顾名思义,此回归器实现了基于每个训练点固定半径 r 内的邻居数量的学习。让我们通过一个实现示例来更好地理解它:
实现示例
在这个示例中,我们将使用 scikit-learn RadiusNeighborsRegressor 在名为 Iris 花数据集的数据集上实现 KNN:
首先,导入 iris 数据集,如下所示:
from sklearn.datasets import load_iris iris = load_iris()
现在,我们需要将数据分成训练数据和测试数据。我们将使用 Sklearn train_test_split 函数将数据分成 70(训练数据)和 20(测试数据)的比例:
X = iris.data[:, :4] y = iris.target from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)
接下来,我们将使用 Sklearn 预处理模块进行数据缩放,如下所示:
from sklearn.preprocessing import StandardScaler scaler = StandardScaler() scaler.fit(X_train) X_train = scaler.transform(X_train) X_test = scaler.transform(X_test)
接下来,从 Sklearn 导入RadiusneighborsRegressor 类,并提供半径的值,如下所示:
import numpy as np from sklearn.neighbors import RadiusNeighborsRegressor knnr_r = RadiusNeighborsRegressor(radius=1) knnr_r.fit(X_train, y_train)
示例
现在,我们可以找到 MSE(均方误差),如下所示:
print ("The MSE is:",format(np.power(y-knnr_r.predict(X),4).mean()))
输出
The MSE is: The MSE is: 5.666666666666667
示例
现在,用它来预测值,如下所示:
X = [[0], [1], [2], [3]] y = [0, 0, 1, 1] from sklearn.neighbors import RadiusNeighborsRegressor knnr_r = RadiusNeighborsRegressor(radius=1) knnr_r.fit(X, y) print(knnr_r.predict([[2.5]]))
输出
[1.]
完整的可运行程序
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:, :4]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
import numpy as np
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius = 1)
knnr_r.fit(X_train, y_train)
print ("The MSE is:",format(np.power(y-knnr_r.predict(X),4).mean()))
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import RadiusNeighborsRegressor
knnr_r = RadiusNeighborsRegressor(radius = 1)
knnr_r.fit(X, y)
print(knnr_r.predict([[2.5]]))
Scikit Learn - 使用朴素贝叶斯进行分类
朴素贝叶斯方法是一组基于应用贝叶斯定理的监督学习算法,其强有力的假设是所有预测器都相互独立,即一个特征在一个类中的存在与同一类中任何其他特征的存在无关。这是一个天真的假设,这就是为什么这些方法被称为朴素贝叶斯方法。
贝叶斯定理陈述了以下关系,以便找到类别的后验概率,即标签和一些观察到的特征的概率,$P\left(\begin{array}{c} Y\arrowvert features\end{array}\right)$。
$$P\left(\begin{array}{c} Y\arrowvert features\end{array}\right)=\left(\frac{P\lgroup Y\rgroup P\left(\begin{array}{c} features\arrowvert Y\end{array}\right)}{P\left(\begin{array}{c} features\end{array}\right)}\right)$$这里,$P\left(\begin{array}{c} Y\arrowvert features\end{array}\right)$ 是类的后验概率。
$P\left(\begin{array}{c} Y\end{array}\right)$ 是类的先验概率。
$P\left(\begin{array}{c} features\arrowvert Y\end{array}\right)$ 是似然,即给定类的预测器的概率。
$P\left(\begin{array}{c} features\end{array}\right)$ 是预测器的先验概率。
Scikit-learn 提供了不同的朴素贝叶斯分类器模型,即高斯、多项式、补充和伯努利。它们的主要区别在于它们对 𝑷$P\left(\begin{array}{c} features\arrowvert Y\end{array}\right)$(即给定类的预测器的概率)的分布所做的假设。
| 序号 | 模型和描述 |
|---|---|
| 1 |
高斯朴素贝叶斯
高斯朴素贝叶斯分类器假设每个标签的数据都来自简单的正态分布。 |
| 2 |
多项式朴素贝叶斯
它假设特征来自简单的多项式分布。 |
| 3 |
伯努利朴素贝叶斯
该模型的假设是特征本质上是二元的(0 和 1)。伯努利朴素贝叶斯分类的一个应用是使用“词袋”模型进行文本分类。 |
| 4 |
补充朴素贝叶斯
它旨在纠正多项式贝叶斯分类器所做的严重假设。这种 NB 分类器适用于不平衡数据集。 |
构建朴素贝叶斯分类器
我们还可以将朴素贝叶斯分类器应用于 Scikit-learn 数据集。在下面的示例中,我们正在应用 GaussianNB 并拟合 Scikit-leran 的 breast_cancer 数据集。
示例
Import Sklearn from sklearn.datasets import load_breast_cancer from sklearn.model_selection import train_test_split data = load_breast_cancer() label_names = data['target_names'] labels = data['target'] feature_names = data['feature_names'] features = data['data'] print(label_names) print(labels[0]) print(feature_names[0]) print(features[0]) train, test, train_labels, test_labels = train_test_split( features,labels,test_size = 0.40, random_state = 42 ) from sklearn.naive_bayes import GaussianNB GNBclf = GaussianNB() model = GNBclf.fit(train, train_labels) preds = GNBclf.predict(test) print(preds)
输出
[ 1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0 1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0 1 1 0 1 1 0 0 0 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 0 0 1 1 0 1 0 1 1 1 1 0 1 1 0 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 0 0 1 1 0 1 ]
上述输出包含一系列 0 和 1,它们基本上是来自肿瘤类别(即恶性和良性)的预测值。
Scikit Learn - 决策树
在本章中,我们将学习 Sklearn 中称为决策树的学习方法。
决策树 (DTs) 是最强大的非参数监督学习方法。它们可以用于分类和回归任务。DTs 的主要目标是创建一个模型,通过学习从数据特征推导出的简单决策规则来预测目标变量值。决策树有两个主要实体;一个是根节点,数据在此处分割;另一个是决策节点或叶子节点,我们在此处获得最终输出。
决策树算法
下面解释了不同的决策树算法:
ID3
它由 Ross Quinlan 于 1986 年开发。它也称为迭代二分器 3。该算法的主要目标是为每个节点找到那些分类特征,这些特征将为分类目标产生最大的信息增益。
它允许树生长到最大尺寸,然后为了提高树对未见数据的处理能力,应用修剪步骤。该算法的输出将是多路树。
C4.5
它是 ID3 的后继者,它动态地定义一个离散属性,该属性将连续属性值划分为一组离散的区间。这就是它取消了分类特征限制的原因。它将 ID3 训练的树转换为一组“IF-THEN”规则。
为了确定应用这些规则的顺序,将首先评估每个规则的准确性。
C5.0
它的工作方式类似于 C4.5,但它使用更少的内存并构建更小的规则集。它比 C4.5 更准确。
CART
它被称为分类和回归树算法。它基本上通过使用特征和阈值来生成二元分割,在每个节点产生最大的信息增益(称为基尼指数)。
同质性取决于基尼指数,基尼指数的值越高,同质性就越高。它类似于 C4.5 算法,但不同之处在于它不计算规则集,也不支持数值目标变量(回归)。
决策树分类
在本例中,决策变量是分类变量。
Sklearn 模块 − Scikit-learn 库提供名为 DecisionTreeClassifier 的模块,用于对数据集执行多类分类。
参数
下表列出了 sklearn.tree.DecisionTreeClassifier 模块使用的参数:
| 序号 | 参数和描述 |
|---|---|
| 1 | criterion − 字符串,可选,默认为 “gini” 它表示用于衡量分割质量的函数。支持的标准是“gini”和“entropy”。默认为 gini,表示基尼不纯度,而 entropy 表示信息增益。 |
| 2 | splitter − 字符串,可选,默认为 “best” 它告诉模型在每个节点选择哪个策略(“best”或“random”)进行分割。 |
| 3 | max_depth − 整数或 None,可选,默认为 None 此参数决定树的最大深度。默认值为 None,这意味着节点将一直扩展,直到所有叶子节点都是纯的,或者所有叶子节点包含的样本数少于 min_smaples_split。 |
| 4 | min_samples_split − 整数,浮点数,可选,默认为 2 此参数提供拆分内部节点所需的最小样本数。 |
| 5 | min_samples_leaf − 整数,浮点数,可选,默认为 1 此参数提供叶节点所需的最小样本数。 |
| 6 | min_weight_fraction_leaf − 浮点数,可选,默认为 0. 使用此参数,模型将获得叶节点所需的权重总和的最小加权分数。 |
| 7 | max_features − 整数,浮点数,字符串或 None,可选,默认为 None 它为模型提供了在寻找最佳分割时要考虑的特征数量。 |
| 8 | random_state − int,RandomState 实例或 None,可选,默认值 = none 此参数表示生成的伪随机数的种子,该种子在洗牌数据时使用。选项如下:
|
| 9 | max_leaf_nodes − 整数或 None,可选,默认为 None 此参数将以最佳优先的方式生成具有 max_leaf_nodes 的树。默认为 none,这意味着将有无限数量的叶子节点。 |
| 10 | min_impurity_decrease − 浮点数,可选,默认为 0. 此值用作节点分割的标准,因为如果此分割引起的杂质减少大于或等于 min_impurity_decrease 值,则模型将分割节点。 |
| 11 | min_impurity_split − 浮点数,默认为 1e-7 它表示树增长中提前停止的阈值。 |
| 12 | class_weight − 字典,字典列表,“balanced”或 None,默认为 None 它表示与类关联的权重。格式为 {class_label: weight}。如果我们使用默认选项,则表示所有类别的权重都为 1。另一方面,如果您选择 class_weight: balanced,它将使用 y 的值来自动调整权重。 |
| 13 | presort − 布尔值,可选,默认为 False 它告诉模型是否预先对数据进行排序,以加快拟合过程中寻找最佳分割的速度。默认为 false,但如果设置为 true,则可能会减慢训练过程。 |
属性
下表列出了 sklearn.tree.DecisionTreeClassifier 模块使用的属性:
| 序号 | 参数和描述 |
|---|---|
| 1 | feature_importances_ − 形状为 =[n_features] 的数组 此属性将返回特征重要性。 |
| 2 | classes_: − 形状为 = [n_classes] 的数组或此类数组的列表 它表示类标签,即单输出问题,或类标签数组列表,即多输出问题。 |
| 3 | max_features_ − 整数 它表示 max_features 参数推断出的值。 |
| 4 | n_classes_ − 整数或列表 它表示类的数量,即单输出问题,或每个输出的类数量列表,即多输出问题。 |
| 5 | n_features_ − 整数 执行 fit() 方法时,它给出特征的数量。 |
| 6 | n_outputs_ − 整数 执行 fit() 方法时,它给出输出的数量。 |
方法
下表列出了 sklearn.tree.DecisionTreeClassifier 模块使用的方法:
| 序号 | 参数和描述 |
|---|---|
| 1 | apply(self, X[, check_input]) 此方法将返回叶子的索引。 |
| 2 | decision_path(self, X[, check_input]) 顾名思义,此方法将返回树中的决策路径。 |
| 3 | fit(self, X, y[, sample_weight, …]) fit() 方法将根据给定的训练集 (X, y) 构建决策树分类器。 |
| 4 | get_depth(self) 顾名思义,此方法将返回决策树的深度。 |
| 5 | get_n_leaves(self) 顾名思义,此方法将返回决策树的叶子数量。 |
| 6 | get_params(self[, deep]) 我们可以使用此方法获取估计器的参数。 |
| 7 | predict(self, X[, check_input]) 它将预测 X 的类值。 |
| 8 | predict_log_proba(self, X) 它将预测我们提供的输入样本 X 的类对数概率。 |
| 9 | predict_proba(self, X[, check_input]) 它将预测我们提供的输入样本 X 的类概率。 |
| 10 | score(self, X, y[, sample_weight]) 顾名思义,score() 方法将返回给定测试数据和标签上的平均精度。 |
| 11 | set_params(self, \*\*params) 我们可以使用此方法设置估计器的参数。 |
实现示例
下面的 Python 脚本将使用 sklearn.tree.DecisionTreeClassifier 模块构建一个分类器,用于根据我们具有 25 个样本和两个特征(“身高”和“头发长度”)的数据集预测男性或女性:
from sklearn import tree from sklearn.model_selection import train_test_split X=[[165,19],[175,32],[136,35],[174,65],[141,28],[176,15] ,[131,32],[166,6],[128,32],[179,10],[136,34],[186,2],[12 6,25],[176,28],[112,38],[169,9],[171,36],[116,25],[196,2 5], [196,38], [126,40], [197,20], [150,25], [140,32],[136,35]] Y=['Man','Woman','Woman','Man','Woman','Man','Woman','Ma n','Woman','Man','Woman','Man','Woman','Woman','Woman',' Man','Woman','Woman','Man', 'Woman', 'Woman', 'Man', 'Man', 'Woman', 'Woman'] data_feature_names = ['height','length of hair'] X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = 0.3, random_state = 1) DTclf = tree.DecisionTreeClassifier() DTclf = clf.fit(X,Y) prediction = DTclf.predict([[135,29]]) print(prediction)
输出
['Woman']
我们还可以通过使用以下 python predict_proba() 方法预测每个类的概率:
示例
prediction = DTclf.predict_proba([[135,29]]) print(prediction)
输出
[[0. 1.]]
决策树回归
在本例中,决策变量是连续变量。
Sklearn 模块 − Scikit-learn 库提供名为 DecisionTreeRegressor 的模块,用于将决策树应用于回归问题。
参数
DecisionTreeRegressor 使用的参数与 DecisionTreeClassifier 模块中使用的参数几乎相同。区别在于 “criterion” 参数。对于 DecisionTreeRegressor 模块,“criterion: 字符串,可选,默认为 “mse””参数具有以下值:
mse − 代表均方误差。它等于方差减少作为特征选择标准。它使用每个终端节点的均值来最小化 L2 损失。
freidman_mse − 它也使用均方误差,但使用了弗里德曼的改进评分。
mae − 代表平均绝对误差。它使用每个终端节点的中位数来最小化 L1 损失。
另一个区别是它没有 ‘class_weight’ 参数。
属性
DecisionTreeRegressor 的属性也与 DecisionTreeClassifier 模块的属性相同。区别在于它没有 ‘classes_’ 和 ‘n_classes_’ 属性。
方法
DecisionTreeRegressor 的方法也与 DecisionTreeClassifier 模块的方法相同。区别在于它没有 ‘predict_log_proba()’ 和 ‘predict_proba()’ 属性。
实现示例
决策树回归模型中的 fit() 方法将采用 y 的浮点值。让我们通过使用 Sklearn.tree.DecisionTreeRegressor 来查看一个简单的实现示例:
from sklearn import tree X = [[1, 1], [5, 5]] y = [0.1, 1.5] DTreg = tree.DecisionTreeRegressor() DTreg = clf.fit(X, y)
拟合后,我们可以使用此回归模型进行预测,如下所示:
DTreg.predict([[4, 5]])
输出
array([1.5])
Scikit Learn - 随机决策树
本章将帮助您了解 Sklearn 中的随机决策树。
随机决策树算法
众所周知,决策树通常通过递归分割数据进行训练,但由于容易过拟合,它们已被转换为随机森林,方法是在数据的各种子样本上训练许多树。sklearn.ensemble 模块包含以下两种基于随机决策树的算法:
随机森林算法
对于正在考虑的每个特征,它计算局部最佳特征/分割组合。在随机森林中,集成中的每个决策树都是从训练集中有放回地抽取的样本构建的,然后从每个样本中获得预测,最后通过投票选择最佳解决方案。它可用于分类和回归任务。
随机森林分类
要创建随机森林分类器,Scikit-learn 模块提供 sklearn.ensemble.RandomForestClassifier。在构建随机森林分类器时,此模块使用的主要参数是 ‘max_features’ 和 ‘n_estimators’。
这里,‘max_features’ 是在分割节点时要考虑的特征随机子集的大小。如果我们将此参数的值选择为 none,则它将考虑所有特征,而不是随机子集。另一方面,n_estimators 是森林中的树木数量。树木数量越多,结果越好。但计算时间也会更长。
实现示例
在下面的示例中,我们使用 sklearn.ensemble.RandomForestClassifier 构建随机森林分类器,并使用 cross_val_score 模块检查其精度。
from sklearn.model_selection import cross_val_score from sklearn.datasets import make_blobs from sklearn.ensemble import RandomForestClassifier X, y = make_blobs(n_samples = 10000, n_features = 10, centers = 100,random_state = 0) RFclf = RandomForestClassifier(n_estimators = 10,max_depth = None,min_samples_split = 2, random_state = 0) scores = cross_val_score(RFclf, X, y, cv = 5) scores.mean()
输出
0.9997
示例
我们还可以使用 sklearn 数据集构建随机森林分类器。在下面的示例中,我们使用 iris 数据集。我们还将找到其精度分数和混淆矩阵。
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
path = "https://archive.ics.uci.edu/ml/machine-learning-database
s/iris/iris.data"
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']
dataset = pd.read_csv(path, names = headernames)
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, 4].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30)
RFclf = RandomForestClassifier(n_estimators = 50)
RFclf.fit(X_train, y_train)
y_pred = RFclf.predict(X_test)
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)
输出
Confusion Matrix:
[[14 0 0]
[ 0 18 1]
[ 0 0 12]]
Classification Report:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 14
Iris-versicolor 1.00 0.95 0.97 19
Iris-virginica 0.92 1.00 0.96 12
micro avg 0.98 0.98 0.98 45
macro avg 0.97 0.98 0.98 45
weighted avg 0.98 0.98 0.98 45
Accuracy: 0.9777777777777777
随机森林回归
要创建随机森林回归,Scikit-learn 模块提供 sklearn.ensemble.RandomForestRegressor。在构建随机森林回归器时,它将使用与 sklearn.ensemble.RandomForestClassifier 使用的参数相同。
实现示例
在下面的示例中,我们使用 sklearn.ensemble.RandomForestregressor 构建随机森林回归器,并使用 predict() 方法预测新值。
from sklearn.ensemble import RandomForestRegressor from sklearn.datasets import make_regression X, y = make_regression(n_features = 10, n_informative = 2,random_state = 0, shuffle = False) RFregr = RandomForestRegressor(max_depth = 10,random_state = 0,n_estimators = 100) RFregr.fit(X, y)
输出
RandomForestRegressor( bootstrap = True, criterion = 'mse', max_depth = 10, max_features = 'auto', max_leaf_nodes = None, min_impurity_decrease = 0.0, min_impurity_split = None, min_samples_leaf = 1, min_samples_split = 2, min_weight_fraction_leaf = 0.0, n_estimators = 100, n_jobs = None, oob_score = False, random_state = 0, verbose = 0, warm_start = False )
拟合后,我们可以从回归模型中进行预测,如下所示:
print(RFregr.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))
输出
[98.47729198]
极端随机树方法
对于正在考虑的每个特征,它都会为分割选择一个随机值。使用极端随机树方法的好处是可以进一步降低模型的方差。使用这些方法的缺点是它会稍微增加偏差。
极端随机树方法分类
要使用极端随机树方法创建分类器,Scikit-learn 模块提供 sklearn.ensemble.ExtraTreesClassifier。它使用与 sklearn.ensemble.RandomForestClassifier 使用的参数相同。唯一的区别在于它们构建树的方式,如上所述。
实现示例
在下面的示例中,我们使用 sklearn.ensemble.ExtraTreeClassifier 构建随机森林分类器,并使用 cross_val_score 模块检查其精度。
from sklearn.model_selection import cross_val_score from sklearn.datasets import make_blobs from sklearn.ensemble import ExtraTreesClassifier X, y = make_blobs(n_samples = 10000, n_features = 10, centers=100,random_state = 0) ETclf = ExtraTreesClassifier(n_estimators = 10,max_depth = None,min_samples_split = 10, random_state = 0) scores = cross_val_score(ETclf, X, y, cv = 5) scores.mean()
输出
1.0
示例
我们还可以使用 sklearn 数据集使用极端随机树方法构建分类器。在下面的示例中,我们使用 Pima-Indian 数据集。
from pandas import read_csv from sklearn.model_selection import KFold from sklearn.model_selection import cross_val_score from sklearn.ensemble import ExtraTreesClassifier path = r"C:\pima-indians-diabetes.csv" headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] data = read_csv(path, names=headernames) array = data.values X = array[:,0:8] Y = array[:,8] seed = 7 kfold = KFold(n_splits=10, random_state=seed) num_trees = 150 max_features = 5 ETclf = ExtraTreesClassifier(n_estimators=num_trees, max_features=max_features) results = cross_val_score(ETclf, X, Y, cv=kfold) print(results.mean())
输出
0.7551435406698566
极端随机树方法回归
要创建**Extra-Tree**回归模型,Scikit-learn模块提供**sklearn.ensemble.ExtraTreesRegressor**。构建随机森林回归器时,它将使用与**sklearn.ensemble.ExtraTreesClassifier**相同的参数。
实现示例
在下面的示例中,我们将应用**sklearn.ensemble.ExtraTreesRegressor**,并使用与创建随机森林回归器时相同的数据。让我们看看输出结果的差异。
from sklearn.ensemble import ExtraTreesRegressor from sklearn.datasets import make_regression X, y = make_regression(n_features = 10, n_informative = 2,random_state = 0, shuffle = False) ETregr = ExtraTreesRegressor(max_depth = 10,random_state = 0,n_estimators = 100) ETregr.fit(X, y)
输出
ExtraTreesRegressor(bootstrap = False, criterion = 'mse', max_depth = 10, max_features = 'auto', max_leaf_nodes = None, min_impurity_decrease = 0.0, min_impurity_split = None, min_samples_leaf = 1, min_samples_split = 2, min_weight_fraction_leaf = 0.0, n_estimators = 100, n_jobs = None, oob_score = False, random_state = 0, verbose = 0, warm_start = False)
示例
拟合后,我们可以从回归模型中进行预测,如下所示:
print(ETregr.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))
输出
[85.50955817]
Scikit Learn - 集成方法
本章,我们将学习Sklearn中的提升方法,这使得能够构建集成模型。
提升方法以增量的方式构建集成模型。其主要原理是通过依次训练每个基础模型估计器来增量构建模型。为了构建强大的集成模型,这些方法基本上结合了多个弱学习器,这些弱学习器在对训练数据的多次迭代中依次进行训练。sklearn.ensemble模块包含以下两种提升方法。
AdaBoost
它是最成功的提升集成方法之一,其关键在于它赋予数据集实例权重的方式。这就是为什么该算法在构建后续模型时需要较少关注这些实例。
AdaBoost分类
要创建AdaBoost分类器,Scikit-learn模块提供**sklearn.ensemble.AdaBoostClassifier**。构建此分类器时,该模块使用的主要参数是**base_estimator**。这里,base_estimator是从中构建提升集成模型的基础估计器的值。如果我们将此参数的值设置为None,则基础估计器将为**DecisionTreeClassifier(max_depth=1)**。
实现示例
在下面的示例中,我们将使用**sklearn.ensemble.AdaBoostClassifier**构建AdaBoost分类器,并预测并检查其得分。
from sklearn.ensemble import AdaBoostClassifier from sklearn.datasets import make_classification X, y = make_classification(n_samples = 1000, n_features = 10,n_informative = 2, n_redundant = 0,random_state = 0, shuffle = False) ADBclf = AdaBoostClassifier(n_estimators = 100, random_state = 0) ADBclf.fit(X, y)
输出
AdaBoostClassifier(algorithm = 'SAMME.R', base_estimator = None, learning_rate = 1.0, n_estimators = 100, random_state = 0)
示例
拟合后,我们可以预测新的值,如下所示:
print(ADBclf.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))
输出
[1]
示例
现在我们可以检查得分,如下所示:
ADBclf.score(X, y)
输出
0.995
示例
我们还可以使用sklearn数据集使用Extra-Tree方法构建分类器。例如,在下面给出的示例中,我们使用Pima-Indian数据集。
from pandas import read_csv from sklearn.model_selection import KFold from sklearn.model_selection import cross_val_score from sklearn.ensemble import AdaBoostClassifier path = r"C:\pima-indians-diabetes.csv" headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] data = read_csv(path, names = headernames) array = data.values X = array[:,0:8] Y = array[:,8] seed = 5 kfold = KFold(n_splits = 10, random_state = seed) num_trees = 100 max_features = 5 ADBclf = AdaBoostClassifier(n_estimators = num_trees, max_features = max_features) results = cross_val_score(ADBclf, X, Y, cv = kfold) print(results.mean())
输出
0.7851435406698566
AdaBoost回归
要使用AdaBoost方法创建回归器,Scikit-learn库提供**sklearn.ensemble.AdaBoostRegressor**。构建回归器时,它将使用与**sklearn.ensemble.AdaBoostClassifier**相同的参数。
实现示例
在下面的示例中,我们将使用**sklearn.ensemble.AdaBoostRegressor**构建AdaBoost回归器,并使用predict()方法预测新值。
from sklearn.ensemble import AdaBoostRegressor from sklearn.datasets import make_regression X, y = make_regression(n_features = 10, n_informative = 2,random_state = 0, shuffle = False) ADBregr = RandomForestRegressor(random_state = 0,n_estimators = 100) ADBregr.fit(X, y)
输出
AdaBoostRegressor(base_estimator = None, learning_rate = 1.0, loss = 'linear', n_estimators = 100, random_state = 0)
示例
拟合后,我们可以从回归模型中进行预测,如下所示:
print(ADBregr.predict([[0, 2, 3, 0, 1, 1, 1, 1, 2, 2]]))
输出
[85.50955817]
梯度提升树
它也称为**梯度提升回归树**(GRBT)。它基本上是将提升推广到任意可微损失函数。它以弱预测模型集成的形式生成预测模型。它可用于回归和分类问题。它们的主要优势在于它们能够自然地处理混合类型数据。
梯度提升树分类
要创建梯度提升树分类器,Scikit-learn模块提供**sklearn.ensemble.GradientBoostingClassifier**。构建此分类器时,该模块使用的主要参数是“loss”。这里,“loss”是要优化的损失函数的值。如果我们选择loss = 'deviance',它指的是具有概率输出的分类的偏差。
另一方面,如果我们将此参数的值设置为'exponential',则它将恢复AdaBoost算法。参数**n_estimators**将控制弱学习器的数量。名为**learning_rate**的超参数(范围为(0.0, 1.0])将通过收缩来控制过拟合。
实现示例
在下面的示例中,我们将使用**sklearn.ensemble.GradientBoostingClassifier**构建梯度提升分类器。我们将此分类器与50个弱学习器拟合。
from sklearn.datasets import make_hastie_10_2 from sklearn.ensemble import GradientBoostingClassifier X, y = make_hastie_10_2(random_state = 0) X_train, X_test = X[:5000], X[5000:] y_train, y_test = y[:5000], y[5000:] GDBclf = GradientBoostingClassifier(n_estimators = 50, learning_rate = 1.0,max_depth = 1, random_state = 0).fit(X_train, y_train) GDBclf.score(X_test, y_test)
输出
0.8724285714285714
示例
我们还可以使用sklearn数据集使用梯度提升分类器构建分类器。在下面的示例中,我们使用Pima-Indian数据集。
from pandas import read_csv from sklearn.model_selection import KFold from sklearn.model_selection import cross_val_score from sklearn.ensemble import GradientBoostingClassifier path = r"C:\pima-indians-diabetes.csv" headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] data = read_csv(path, names = headernames) array = data.values X = array[:,0:8] Y = array[:,8] seed = 5 kfold = KFold(n_splits = 10, random_state = seed) num_trees = 100 max_features = 5 ADBclf = GradientBoostingClassifier(n_estimators = num_trees, max_features = max_features) results = cross_val_score(ADBclf, X, Y, cv = kfold) print(results.mean())
输出
0.7946582356674234
梯度提升树回归
要使用梯度提升树方法创建回归器,Scikit-learn库提供**sklearn.ensemble.GradientBoostingRegressor**。它可以通过参数名称loss指定回归的损失函数。loss的默认值为'ls'。
实现示例
在下面的示例中,我们将使用**sklearn.ensemble.GradientBoostingRegressor**构建梯度提升回归器,并使用mean_squared_error()方法找到均方误差。
import numpy as np from sklearn.metrics import mean_squared_error from sklearn.datasets import make_friedman1 from sklearn.ensemble import GradientBoostingRegressor X, y = make_friedman1(n_samples = 2000, random_state = 0, noise = 1.0) X_train, X_test = X[:1000], X[1000:] y_train, y_test = y[:1000], y[1000:] GDBreg = GradientBoostingRegressor(n_estimators = 80, learning_rate=0.1, max_depth = 1, random_state = 0, loss = 'ls').fit(X_train, y_train)
拟合后,我们可以找到均方误差,如下所示:
mean_squared_error(y_test, GDBreg.predict(X_test))
输出
5.391246106657164
Scikit Learn - 聚类方法
在这里,我们将学习Sklearn中的聚类方法,这将有助于识别数据样本中的任何相似性。
聚类方法是最有用的无监督机器学习方法之一,用于查找数据样本之间的相似性和关系模式。之后,它们将这些样本聚类到具有基于特征的相似性的组中。聚类确定当前未标记数据中的内在分组,因此它很重要。
Scikit-learn库使用**sklearn.cluster**对未标记数据进行聚类。在此模块下,scikit-learn包含以下聚类方法:
KMeans
此算法计算质心并进行迭代,直到找到最佳质心。它需要指定聚类数量,这就是为什么它假设它们已经知道。该算法的主要逻辑是通过最小化称为惯性的标准来分离样本到n个方差相等的组中来对数据进行聚类。算法识别的聚类数量用'K'表示。
Scikit-learn使用**sklearn.cluster.KMeans**模块执行K均值聚类。在计算聚类中心和惯性值时,名为**sample_weight**的参数允许**sklearn.cluster.KMeans**模块为某些样本分配更大的权重。
亲和传播
此算法基于不同样本对之间“消息传递”的概念,直到收敛。它不需要在运行算法之前指定聚类数量。该算法的时间复杂度为O(N²T),这是其最大的缺点。
Scikit-learn使用**sklearn.cluster.AffinityPropagation**模块执行亲和传播聚类。
均值漂移
此算法主要发现样本平滑密度中的**块**。它通过将点移向数据点的最高密度来迭代地将数据点分配给聚类。它不依赖于名为**bandwidth**的参数来指示要搜索的区域的大小,而是自动设置聚类数量。
Scikit-learn使用**sklearn.cluster.MeanShift**模块执行均值漂移聚类。
谱聚类
在聚类之前,此算法基本上使用数据相似矩阵的特征值(即谱)来在较少的维度上执行降维。当聚类数量很大时,不建议使用此算法。
Scikit-learn使用**sklearn.cluster.SpectralClustering**模块执行谱聚类。
层次聚类
此算法通过连续合并或拆分聚类来构建嵌套聚类。此聚类层次结构表示为树状图(即树)。它分为以下两类:
**凝聚层次算法** - 在这种层次算法中,每个数据点都被视为单个聚类。然后,它连续地将聚类对聚合在一起。这使用自下而上的方法。
**分裂层次算法** - 在这种层次算法中,所有数据点都被视为一个大的聚类。在聚类过程中,它通过使用自上而下的方法将一个大的聚类划分为各种小的聚类。
Scikit-learn使用**sklearn.cluster.AgglomerativeClustering**模块执行凝聚层次聚类。
DBSCAN
它代表**“基于密度的噪声应用空间聚类”**。此算法基于“聚类”和“噪声”的直观概念,即聚类是数据空间中低密度区域中被低密度数据点区域分隔开的密集区域。
Scikit-learn使用**sklearn.cluster.DBSCAN**模块执行DBSCAN聚类。此算法使用两个重要参数,即min_samples和eps来定义密集。
参数**min_samples**的值越高或参数eps的值越低,表明形成聚类所需的较高数据点密度。
OPTICS
它代表**“排序点以识别聚类结构”**。此算法还在空间数据中查找基于密度的聚类。它的基本工作逻辑类似于DBSCAN。
它通过以这种方式对数据库的点进行排序,使得空间上最接近的点在排序中成为相邻点,从而解决了DBSCAN算法的一个主要弱点——在不同密度的数据中检测有意义的聚类的问题。
Scikit-learn使用**sklearn.cluster.OPTICS**模块执行OPTICS聚类。
BIRCH
它代表使用层次结构的平衡迭代减少和聚类。它用于对大型数据集执行层次聚类。它为给定数据构建一棵名为**CFT**(即**特征特征树**)的树。
CFT 的优点是称为 CF(特征特征)节点的数据节点保存了聚类所需的必要信息,这进一步避免了需要将整个输入数据保存在内存中。
Scikit-learn使用**sklearn.cluster.Birch**模块执行BIRCH聚类。
比较聚类算法
下表将对scikit-learn中的聚类算法(基于参数、可扩展性和度量)进行比较。
| 序号 | 算法名称 | 参数 | 可扩展性 | 使用的度量 |
|---|---|---|---|---|
| 1 | K-Means | 聚类数 | 非常大的n_samples | 点之间的距离。 |
| 2 | 亲和传播 | 阻尼 | 它不能随着n_samples扩展 | 图距离 |
| 3 | 均值漂移 | 带宽 | 它不能随着n_samples扩展。 | 点之间的距离。 |
| 4 | 谱聚类 | 聚类数 | 中等程度的n_samples可扩展性。小程度的n_clusters可扩展性。 | 图距离 |
| 5 | 层次聚类 | 距离阈值或聚类数 | 大的n_samples 大的n_clusters | 点之间的距离。 |
| 6 | DBSCAN | 邻域大小 | 非常大的n_samples和中等n_clusters。 | 最近点距离 |
| 7 | OPTICS | 最小聚类成员资格 | 非常大的n_samples和大的n_clusters。 | 点之间的距离。 |
| 8 | BIRCH | 阈值,分支因子 | 大的n_samples 大的n_clusters | 点之间的欧几里德距离。 |
Scikit-learn数字数据集上的K-Means聚类
在这个例子中,我们将对数字数据集应用K-means聚类。此算法将在不使用原始标签信息的情况下识别相似的数字。实现是在Jupyter Notebook上完成的。
%matplotlib inline import matplotlib.pyplot as plt import seaborn as sns; sns.set() import numpy as np from sklearn.cluster import KMeans from sklearn.datasets import load_digits digits = load_digits() digits.data.shape
输出
1797, 64)
此输出显示数字数据集具有1797个样本和64个特征。
示例
现在,执行K-Means聚类,如下所示:
kmeans = KMeans(n_clusters = 10, random_state = 0) clusters = kmeans.fit_predict(digits.data) kmeans.cluster_centers_.shape
输出
(10, 64)
此输出显示K-means聚类创建了10个具有64个特征的聚类。
示例
fig, ax = plt.subplots(2, 5, figsize = (8, 3)) centers = kmeans.cluster_centers_.reshape(10, 8, 8) for axi, center in zip(ax.flat, centers): axi.set(xticks = [], yticks = []) axi.imshow(center, interpolation = 'nearest', cmap = plt.cm.binary)
输出
下面的输出包含显示K-Means聚类学习到的聚类中心的图像。
接下来,下面的Python脚本将学习到的聚类标签(通过K-Means)与其中找到的真实标签匹配:
from scipy.stats import mode labels = np.zeros_like(clusters) for i in range(10): mask = (clusters == i) labels[mask] = mode(digits.target[mask])[0]
我们还可以使用下面提到的命令来检查准确性。
from sklearn.metrics import accuracy_score accuracy_score(digits.target, labels)
输出
0.7935447968836951
完整的实现示例
%matplotlib inline import matplotlib.pyplot as plt import seaborn as sns; sns.set() import numpy as np from sklearn.cluster import KMeans from sklearn.datasets import load_digits digits = load_digits() digits.data.shape kmeans = KMeans(n_clusters = 10, random_state = 0) clusters = kmeans.fit_predict(digits.data) kmeans.cluster_centers_.shape fig, ax = plt.subplots(2, 5, figsize = (8, 3)) centers = kmeans.cluster_centers_.reshape(10, 8, 8) for axi, center in zip(ax.flat, centers): axi.set(xticks=[], yticks = []) axi.imshow(center, interpolation = 'nearest', cmap = plt.cm.binary) from scipy.stats import mode labels = np.zeros_like(clusters) for i in range(10): mask = (clusters == i) labels[mask] = mode(digits.target[mask])[0] from sklearn.metrics import accuracy_score accuracy_score(digits.target, labels)
Scikit Learn - 聚类性能评估
有各种函数可以帮助我们评估聚类算法的性能。
以下是Scikit-learn提供的一些重要且最常用的用于评估聚类性能的函数:
调整后的Rand指数
Rand指数是一个函数,它计算两个聚类之间的相似性度量。对于此计算,Rand指数考虑所有样本对,并计算在预测和真实聚类中被分配到相似或不同聚类的对。之后,使用以下公式将原始Rand指数得分“按机会调整”为调整后的Rand指数得分:
$$Adjusted\:RI=\left(RI-Expected_{-}RI\right)/\left(max\left(RI\right)-Expected_{-}RI\right)$$它有两个参数,即**labels_true**(它是地面真实类标签)和**labels_pred**(是要评估的聚类标签)。
示例
from sklearn.metrics.cluster import adjusted_rand_score labels_true = [0, 0, 1, 1, 1, 1] labels_pred = [0, 0, 2, 2, 3, 3] adjusted_rand_score(labels_true, labels_pred)
输出
0.4444444444444445
完美的标记得分将为1,而错误的标记或独立的标记得分将为0或负数。
基于互信息的得分
互信息是一个计算两个分配之间一致性的函数。它忽略排列。以下是可用版本:
归一化互信息 (NMI)
Scikit-learn 包含 **sklearn.metrics.normalized_mutual_info_score** 模块。
示例
from sklearn.metrics.cluster import normalized_mutual_info_score labels_true = [0, 0, 1, 1, 1, 1] labels_pred = [0, 0, 2, 2, 3, 3] normalized_mutual_info_score (labels_true, labels_pred)
输出
0.7611702597222881
调整后的互信息 (AMI)
Scikit-learn 包含 **sklearn.metrics.adjusted_mutual_info_score** 模块。
示例
from sklearn.metrics.cluster import adjusted_mutual_info_score labels_true = [0, 0, 1, 1, 1, 1] labels_pred = [0, 0, 2, 2, 3, 3] adjusted_mutual_info_score (labels_true, labels_pred)
输出
0.4444444444444448
Fowlkes-Mallows 得分
Fowlkes-Mallows 函数测量一组点的两个聚类的相似性。它可以定义为成对精确度和召回率的几何平均数。
数学公式:
$$FMS=\frac{TP}{\sqrt{\left(TP+FP\right)\left(TP+FN\right)}}$$这里,**TP = 真阳性** - 真实标签和预测标签中都属于相同聚类的点对数量。
**FP = 假阳性** - 真实标签中属于相同聚类但在预测标签中不属于相同聚类的点对数量。
**FN = 假阴性** - 预测标签中属于相同聚类但在真实标签中不属于相同聚类的点对数量。
Scikit-learn 包含 **sklearn.metrics.fowlkes_mallows_score** 模块。
示例
from sklearn.metrics.cluster import fowlkes_mallows_score labels_true = [0, 0, 1, 1, 1, 1] labels_pred = [0, 0, 2, 2, 3, 3] fowlkes_mallows__score (labels_true, labels_pred)
输出
0.6546536707079771
轮廓系数
轮廓函数将使用每个样本的平均类内距离和平均最近类距离来计算所有样本的平均轮廓系数。
数学公式:
$$S=\left(b-a\right)/max\left(a,b\right)$$这里,a 是类内距离。
而 b 是平均最近类距离。
Scikit-learn 包含 **sklearn.metrics.silhouette_score** 模块。
示例
from sklearn import metrics.silhouette_score from sklearn.metrics import pairwise_distances from sklearn import datasets import numpy as np from sklearn.cluster import KMeans dataset = datasets.load_iris() X = dataset.data y = dataset.target kmeans_model = KMeans(n_clusters = 3, random_state = 1).fit(X) labels = kmeans_model.labels_ silhouette_score(X, labels, metric = 'euclidean')
输出
0.5528190123564091
列联表
此矩阵将报告每对可靠的 (真实值, 预测值) 的交集基数。分类问题的混淆矩阵是一个方形列联表。
Scikit-learn 包含 **sklearn.metrics.contingency_matrix** 模块。
示例
from sklearn.metrics.cluster import contingency_matrix x = ["a", "a", "a", "b", "b", "b"] y = [1, 1, 2, 0, 1, 2] contingency_matrix(x, y)
输出
array([ [0, 2, 1], [1, 1, 1] ])
上面输出的第一行显示,在真实聚类为“a”的三个样本中,没有一个在 0 中,两个在 1 中,一个在 2 中。另一方面,第二行显示,在真实聚类为“b”的三个样本中,一个在 0 中,一个在 1 中,一个在 2 中。
Scikit-learn - 使用 PCA 的降维
降维是一种无监督机器学习方法,用于通过选择一组主要特征来减少每个数据样本的特征变量数量。主成分分析 (PCA) 是流行的降维算法之一。
精确 PCA
**主成分分析** (PCA) 用于使用数据的**奇异值分解** (SVD) 进行线性降维,以将其投影到低维空间。在使用 PCA 进行分解时,在应用 SVD 之前,输入数据对于每个特征都被居中,但未缩放。
Scikit-learn ML 库提供 **sklearn.decomposition.PCA** 模块,该模块实现为一个转换器对象,在其 fit() 方法中学习 n 个成分。它也可以用于将新数据投影到这些成分上。
示例
下面的示例将使用 sklearn.decomposition.PCA 模块从 Pima 印第安人糖尿病数据集查找最佳的 5 个主成分。
from pandas import read_csv
from sklearn.decomposition import PCA
path = r'C:\Users\Leekha\Desktop\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', ‘class']
dataframe = read_csv(path, names = names)
array = dataframe.values
X = array[:,0:8]
Y = array[:,8]
pca = PCA(n_components = 5)
fit = pca.fit(X)
print(("Explained Variance: %s") % (fit.explained_variance_ratio_))
print(fit.components_)
输出
Explained Variance: [0.88854663 0.06159078 0.02579012 0.01308614 0.00744094] [ [-2.02176587e-03 9.78115765e-02 1.60930503e-02 6.07566861e-029.93110844e-01 1.40108085e-02 5.37167919e-04 -3.56474430e-03] [-2.26488861e-02 -9.72210040e-01 -1.41909330e-01 5.78614699e-029.46266913e-02 -4.69729766e-02 -8.16804621e-04 -1.40168181e-01] [-2.24649003e-02 1.43428710e-01 -9.22467192e-01 -3.07013055e-012.09773019e-02 -1.32444542e-01 -6.39983017e-04 -1.25454310e-01] [-4.90459604e-02 1.19830016e-01 -2.62742788e-01 8.84369380e-01-6.55503615e-02 1.92801728e-01 2.69908637e-03 -3.01024330e-01] [ 1.51612874e-01 -8.79407680e-02 -2.32165009e-01 2.59973487e-01-1.72312241e-04 2.14744823e-02 1.64080684e-03 9.20504903e-01] ]
增量 PCA
**增量主成分分析** (IPCA) 用于解决主成分分析 (PCA) 最大的限制,即 PCA 只支持批量处理,这意味着所有要处理的输入数据都必须适合内存。
Scikit-learn ML 库提供 **sklearn.decomposition.IPCA** 模块,该模块可以通过在其 **partial_fit** 方法上对顺序获取的数据块进行处理,或者通过启用使用 **np.memmap**(内存映射文件)来实现 Out-of-Core PCA,而无需将整个文件加载到内存中。
与 PCA 相同,在使用 IPCA 进行分解时,在应用 SVD 之前,输入数据对于每个特征都被居中,但未缩放。
示例
下面的示例将在 Sklearn 数字数据集上使用 **sklearn.decomposition.IPCA** 模块。
from sklearn.datasets import load_digits from sklearn.decomposition import IncrementalPCA X, _ = load_digits(return_X_y = True) transformer = IncrementalPCA(n_components = 10, batch_size = 100) transformer.partial_fit(X[:100, :]) X_transformed = transformer.fit_transform(X) X_transformed.shape
输出
(1797, 10)
在这里,我们可以对较小的批次数据进行部分拟合(就像我们每批 100 个一样),或者您可以让 **fit()** 函数将数据分成批次。
核 PCA
核主成分分析是 PCA 的扩展,它使用核实现非线性降维。它支持 **transform** 和 **inverse_transform**。
Scikit-learn ML 库提供 **sklearn.decomposition.KernelPCA** 模块。
示例
下面的示例将在 Sklearn 数字数据集上使用 **sklearn.decomposition.KernelPCA** 模块。我们使用 sigmoid 核。
from sklearn.datasets import load_digits from sklearn.decomposition import KernelPCA X, _ = load_digits(return_X_y = True) transformer = KernelPCA(n_components = 10, kernel = 'sigmoid') X_transformed = transformer.fit_transform(X) X_transformed.shape
输出
(1797, 10)
使用随机 SVD 的 PCA
使用随机 SVD 的主成分分析 (PCA) 用于将数据投影到低维空间,同时保留大部分方差,方法是丢弃与较低奇异值相关的成分的奇异向量。在这里,**sklearn.decomposition.PCA** 模块以及可选参数 **svd_solver='randomized'** 将非常有用。
示例
下面的示例将使用带有可选参数 svd_solver='randomized' 的 **sklearn.decomposition.PCA** 模块从 Pima 印第安人糖尿病数据集查找最佳的 7 个主成分。
from pandas import read_csv
from sklearn.decomposition import PCA
path = r'C:\Users\Leekha\Desktop\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names = names)
array = dataframe.values
X = array[:,0:8]
Y = array[:,8]
pca = PCA(n_components = 7,svd_solver = 'randomized')
fit = pca.fit(X)
print(("Explained Variance: %s") % (fit.explained_variance_ratio_))
print(fit.components_)
输出
Explained Variance: [8.88546635e-01 6.15907837e-02 2.57901189e-02 1.30861374e-027.44093864e-03 3.02614919e-03 5.12444875e-04] [ [-2.02176587e-03 9.78115765e-02 1.60930503e-02 6.07566861e-029.93110844e-01 1.40108085e-02 5.37167919e-04 -3.56474430e-03] [-2.26488861e-02 -9.72210040e-01 -1.41909330e-01 5.78614699e-029.46266913e-02 -4.69729766e-02 -8.16804621e-04 -1.40168181e-01] [-2.24649003e-02 1.43428710e-01 -9.22467192e-01 -3.07013055e-012.09773019e-02 -1.32444542e-01 -6.39983017e-04 -1.25454310e-01] [-4.90459604e-02 1.19830016e-01 -2.62742788e-01 8.84369380e-01-6.55503615e-02 1.92801728e-01 2.69908637e-03 -3.01024330e-01] [ 1.51612874e-01 -8.79407680e-02 -2.32165009e-01 2.59973487e-01-1.72312241e-04 2.14744823e-02 1.64080684e-03 9.20504903e-01] [-5.04730888e-03 5.07391813e-02 7.56365525e-02 2.21363068e-01-6.13326472e-03 -9.70776708e-01 -2.02903702e-03 -1.51133239e-02] [ 9.86672995e-01 8.83426114e-04 -1.22975947e-03 -3.76444746e-041.42307394e-03 -2.73046214e-03 -6.34402965e-03 -1.62555343e-01] ]