Scikit-Learn - 支持向量机

本章讨论一种称为支持向量机 (SVM) 的机器学习方法。

介绍

支持向量机 (SVM) 是一种强大而灵活的监督式机器学习方法，用于分类、回归和异常值检测。SVM 在高维空间中非常有效，通常用于分类问题。SVM 广受欢迎且内存效率高，因为它们在决策函数中使用了训练点的子集。

SVM 的主要目标是将数据集划分为多个类别，以便找到一个**最大间隔超平面 (MMH)**，这可以通过以下两个步骤完成：

支持向量机将首先迭代生成超平面，以最佳方式分离类别。
之后，它将选择正确分离类别的超平面。

SVM 中的一些重要概念如下：

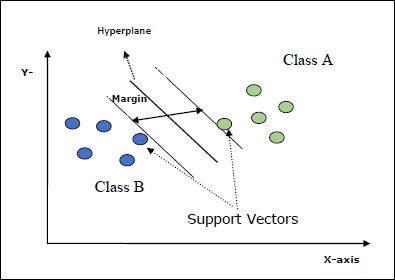
**支持向量** - 可以定义为最靠近超平面的数据点。支持向量有助于确定分离线。
**超平面** - 分割具有不同类别的对象集的决策平面或空间。
**间隔** - 不同类别最靠近数据点之间的两条线之间的间隙称为间隔。

以下图表将让您深入了解这些 SVM 概念：

Scikit-learn 中的 SVM 支持稀疏和密集样本向量作为输入。

SVM 的分类

Scikit-learn 提供了三个类，即**SVC、NuSVC** 和**LinearSVC**，它们可以执行多类分类。

SVC

它是 C 支持向量分类，其实现基于**libsvm**。Scikit-learn 使用的模块是**sklearn.svm.SVC**。此类根据一对一方案处理多类支持。

参数

下表包含**sklearn.svm.SVC** 类使用的参数：

序号	参数及描述
1	C - float，可选，默认值 = 1.0 它是误差项的惩罚参数。
2	kernel - string，可选，默认值 = 'rbf' 此参数指定算法中要使用的内核类型。我们可以从以下选项中选择一个：'linear'、'poly'、'rbf'、'sigmoid'、'precomputed'。内核的默认值为'rbf'。
3	degree - int，可选，默认值 = 3 它表示“poly”内核函数的度数，其他所有内核都会忽略它。
4	gamma - {'scale'、'auto'} 或 float，它是内核“rbf”、“poly”和“sigmoid”的内核系数。
5	可选默认值 - = 'scale' 如果您选择默认值，即 gamma = 'scale'，则 SVC 使用的 gamma 值为 1/(𝑛_𝑓𝑒𝑎𝑡𝑢𝑟𝑒𝑠∗𝑋.𝑣𝑎𝑟())。另一方面，如果 gamma = 'auto'，则它使用 1/𝑛_𝑓𝑒𝑎𝑡𝑢𝑟𝑒𝑠。
6	coef0 - float，可选，默认值 = 0.0 内核函数中的一个独立项，仅在“poly”和“sigmoid”中有效。
7	tol - float，可选，默认值 = 1.e-3 此参数表示迭代的停止条件。
8	shrinking - Boolean，可选，默认值 = True 此参数表示我们是否要使用收缩启发式方法。
9	verbose - Boolean，默认值：false 它启用或禁用详细输出。其默认值为 false。
10	probability - boolean，可选，默认值 = true 此参数启用或禁用概率估计。默认值为 false，但在调用 fit 之前必须启用它。
11	max_iter - int，可选，默认值 = -1 顾名思义，它表示求解器中的最大迭代次数。值 -1 表示迭代次数没有限制。
12	cache_size - float，可选此参数将指定内核缓存的大小。该值将以 MB（兆字节）为单位。
13	random_state - int、RandomState 实例或 None，可选，默认值 = none 此参数表示用于在洗牌数据时生成的伪随机数的种子。选项如下： int - 在这种情况下，random_state 是随机数生成器使用的种子。 RandomState 实例 - 在这种情况下，random_state 是随机数生成器。 None - 在这种情况下，随机数生成器是 np.random 使用的 RandonState 实例。
14	class_weight - {dict、'balanced'}，可选此参数将类 j 的参数 C 设置为 𝑐𝑙𝑎𝑠𝑠_𝑤𝑒𝑖𝑔ℎ𝑡[𝑗]∗𝐶 用于 SVC。如果我们使用默认选项，则意味着所有类都应该具有权重 1。另一方面，如果您选择*class_weight:balanced*，它将使用 y 的值来自动调整权重。
15	decision_function_shape - 'ovo'、'ovr'，默认值 = 'ovr' 此参数将决定算法是否返回形状为所有其他分类器的'ovr'（一对多）决策函数，或 libsvm 的原始ovo（一对一）决策函数。
16	break_ties - boolean，可选，默认值 = false True - predict 将根据 decision_function 的置信度值打破平局 False - predict 将返回平局类中的第一个类。

属性

下表包含**sklearn.svm.SVC** 类使用的属性：

序号	属性及描述
1	support_ - 类似数组，形状 = [n_SV] 它返回支持向量的索引。
2	support_vectors_ - 类似数组，形状 = [n_SV, n_features] 它返回支持向量。
3	n_support_ - 类似数组，dtype=int32，形状 = [n_class] 它表示每个类的支持向量数量。
4	dual_coef_ - 数组，形状 = [n_class-1,n_SV] 这些是决策函数中支持向量的系数。
5	coef_ - 数组，形状 = [n_class * (n_class-1)/2, n_features] 此属性仅在使用线性内核时可用，它提供了分配给特征的权重。
6	intercept_ - 数组，形状 = [n_class * (n_class-1)/2] 它表示决策函数中的独立项（常数）。
7	fit_status_ - int 如果正确拟合，则输出为 0。如果拟合不正确，则输出为 1。
8	classes_ - 形状为 [n_classes] 的数组它给出类的标签。

实现示例

与其他分类器一样，SVC 也必须使用以下两个数组进行拟合：

包含训练样本的数组X。其大小为 [n_samples, n_features]。
包含训练样本的目标值，即类标签的数组Y。其大小为 [n_samples]。

以下 Python 脚本使用sklearn.svm.SVC 类：

import numpy as np
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
from sklearn.svm import SVC
SVCClf = SVC(kernel = 'linear',gamma = 'scale', shrinking = False,)
SVCClf.fit(X, y)

输出

SVC(C = 1.0, cache_size = 200, class_weight = None, coef0 = 0.0,
   decision_function_shape = 'ovr', degree = 3, gamma = 'scale', kernel = 'linear',
   max_iter = -1, probability = False, random_state = None, shrinking = False,
   tol = 0.001, verbose = False)

示例

现在，一旦拟合，我们就可以借助以下 Python 脚本获取权重向量：

SVCClf.coef_

输出

array([[0.5, 0.5]])

示例

类似地，我们可以获取其他属性的值，如下所示：

SVCClf.predict([[-0.5,-0.8]])

输出

array([1])

示例

SVCClf.n_support_

输出

array([1, 1])

示例

SVCClf.support_vectors_

输出

array(
   [
      [-1., -1.],
      [ 1., 1.]
   ]
)

示例

SVCClf.support_

输出

array([0, 2])

示例

SVCClf.intercept_

输出

array([-0.])

示例

SVCClf.fit_status_

输出

NuSVC

NuSVC 是 Nu 支持向量分类。它是 Scikit-learn 提供的另一个可以执行多类分类的类。它类似于 SVC，但 NuSVC 接受略微不同的参数集。与 SVC 不同的参数如下：

nu - float，可选，默认值 = 0.5

它表示训练误差分数的上限和支持向量分数的下限。其值应在 (o,1] 的区间内。

其余参数和属性与 SVC 相同。

实现示例

我们也可以使用sklearn.svm.NuSVC 类实现相同的示例。

import numpy as np
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
from sklearn.svm import NuSVC
NuSVCClf = NuSVC(kernel = 'linear',gamma = 'scale', shrinking = False,)
NuSVCClf.fit(X, y)

输出

NuSVC(cache_size = 200, class_weight = None, coef0 = 0.0,
   decision_function_shape = 'ovr', degree = 3, gamma = 'scale', kernel = 'linear',
   max_iter = -1, nu = 0.5, probability = False, random_state = None,
   shrinking = False, tol = 0.001, verbose = False)

我们可以像在 SVC 中一样获取其余属性的输出。

LinearSVC

它是线性支持向量分类。它类似于具有 kernel = 'linear' 的 SVC。它们之间的区别在于LinearSVC 是根据 liblinear 实现的，而 SVC 是在libsvm 中实现的。这就是LinearSVC 在惩罚和损失函数的选择方面具有更大灵活性的原因。它还可以更好地扩展到大量样本。

如果我们谈论它的参数和属性，那么它不支持'kernel'，因为它被假定为线性，并且它也缺少一些属性，例如support_、support_vectors_、n_support_、fit_status_ 和dual_coef_。

但是，它支持penalty 和loss 参数，如下所示：

penalty - string，L1 或 L2（默认值 = 'L2'）

此参数用于指定惩罚（正则化）中使用的范数（L1 或 L2）。
loss - string，hinge、squared_hinge（默认值 = squared_hinge）

它表示损失函数，其中“hinge”是标准 SVM 损失，“squared_hinge”是 hinge 损失的平方。

实现示例

以下 Python 脚本使用sklearn.svm.LinearSVC 类：

from sklearn.svm import LinearSVC
from sklearn.datasets import make_classification
X, y = make_classification(n_features = 4, random_state = 0)
LSVCClf = LinearSVC(dual = False, random_state = 0, penalty = 'l1',tol = 1e-5)
LSVCClf.fit(X, y)

输出

LinearSVC(C = 1.0, class_weight = None, dual = False, fit_intercept = True,
   intercept_scaling = 1, loss = 'squared_hinge', max_iter = 1000,
   multi_class = 'ovr', penalty = 'l1', random_state = 0, tol = 1e-05, verbose = 0)

示例

现在，一旦拟合，模型就可以预测新值，如下所示：

LSVCClf.predict([[0,0,0,0]])

输出

[1]

示例

对于上述示例，我们可以借助以下 Python 脚本获取权重向量：

LSVCClf.coef_

输出

[[0. 0. 0.91214955 0.22630686]]

示例

类似地，我们可以借助以下 Python 脚本获取截距的值：

LSVCClf.intercept_

输出

[0.26860518]

SVM 回归

如前所述，SVM 用于分类和回归问题。Scikit-learn 的支持向量分类 (SVC) 方法也可以扩展到解决回归问题。该扩展方法称为支持向量回归 (SVR)。

SVM 和 SVR 之间的基本相似性

SVC 创建的模型仅依赖于训练数据的一个子集。为什么？因为构建模型的成本函数不关心位于间隔之外的训练数据点。

而 SVR（支持向量回归）生成的模型也仅依赖于训练数据的一个子集。为什么？因为构建模型的成本函数会忽略任何靠近模型预测的训练数据点。

Scikit-learn 提供了三个类，即**SVR、NuSVR 和 LinearSVR**，作为 SVR 的三种不同实现。

SVR

它是 Epsilon 支持向量回归，其实现基于**libsvm**。与SVC 相反，模型中有两个自由参数，即'C' 和'epsilon'。

epsilon - float，可选，默认值 = 0.1

它表示 epsilon-SVR 模型中的 epsilon，并指定 epsilon 管，在该管内，在训练损失函数中，对预测值与实际值之间的距离在 epsilon 内的点不关联任何惩罚。

其余参数和属性与我们在SVC 中使用的类似。

实现示例

以下 Python 脚本使用sklearn.svm.SVR 类：

from sklearn import svm
X = [[1, 1], [2, 2]]
y = [1, 2]
SVRReg = svm.SVR(kernel = ’linear’, gamma = ’auto’)
SVRReg.fit(X, y)

输出

SVR(C = 1.0, cache_size = 200, coef0 = 0.0, degree = 3, epsilon = 0.1, gamma = 'auto',
   kernel = 'linear', max_iter = -1, shrinking = True, tol = 0.001, verbose = False)

示例

现在，一旦拟合，我们就可以借助以下 Python 脚本获取权重向量：

SVRReg.coef_

输出

array([[0.4, 0.4]])

示例

类似地，我们可以获取其他属性的值，如下所示：

SVRReg.predict([[1,1]])

输出

array([1.1])

类似地，我们也可以获取其他属性的值。

NuSVR

NuSVR 是 Nu 支持向量回归。它类似于 NuSVC，但 NuSVR 使用参数nu来控制支持向量的数量。此外，与 NuSVC 中nu替换 C 参数不同，这里它替换了epsilon。

实现示例

以下 Python 脚本使用sklearn.svm.SVR 类：

from sklearn.svm import NuSVR
import numpy as np
n_samples, n_features = 20, 15
np.random.seed(0)
y = np.random.randn(n_samples)
X = np.random.randn(n_samples, n_features)
NuSVRReg = NuSVR(kernel = 'linear', gamma = 'auto',C = 1.0, nu = 0.1)^M
NuSVRReg.fit(X, y)

输出

NuSVR(C = 1.0, cache_size = 200, coef0 = 0.0, degree = 3, gamma = 'auto',
   kernel = 'linear', max_iter = -1, nu = 0.1, shrinking = True, tol = 0.001,
   verbose = False)

示例

现在，一旦拟合，我们就可以借助以下 Python 脚本获取权重向量：

NuSVRReg.coef_

输出

array(
   [
      [-0.14904483, 0.04596145, 0.22605216, -0.08125403, 0.06564533,
      0.01104285, 0.04068767, 0.2918337 , -0.13473211, 0.36006765,
      -0.2185713 , -0.31836476, -0.03048429, 0.16102126, -0.29317051]
   ]
)

类似地，我们也可以获取其他属性的值。

LinearSVR

它是线性支持向量回归。它类似于具有 kernel = 'linear' 的 SVR。它们之间的区别在于LinearSVR是用liblinear实现的，而 SVC是用libsvm实现的。这就是LinearSVR在惩罚和损失函数的选择方面具有更多灵活性的原因。它也更适合于大量样本。

但是，它支持以下'loss'参数：

loss - 字符串，可选，默认值 = 'epsilon_insensitive'

它表示损失函数，其中 epsilon_insensitive 损失是 L1 损失，而平方 epsilon_insensitive 损失是 L2 损失。

实现示例

以下 Python 脚本使用sklearn.svm.LinearSVR类：

from sklearn.svm import LinearSVR
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 4, random_state = 0)
LSVRReg = LinearSVR(dual = False, random_state = 0,
loss = 'squared_epsilon_insensitive',tol = 1e-5)
LSVRReg.fit(X, y)

输出

LinearSVR(
   C=1.0, dual=False, epsilon=0.0, fit_intercept=True,
   intercept_scaling=1.0, loss='squared_epsilon_insensitive',
   max_iter=1000, random_state=0, tol=1e-05, verbose=0
)

示例

现在，一旦拟合，模型就可以预测新值，如下所示：

LSRReg.predict([[0,0,0,0]])

输出

array([-0.01041416])

示例

对于上述示例，我们可以借助以下 Python 脚本获取权重向量：

LSRReg.coef_

输出

array([20.47354746, 34.08619401, 67.23189022, 87.47017787])

示例

类似地，我们可以借助以下 Python 脚本获取截距的值：

LSRReg.intercept_

输出

array([-0.01041416])

打印页面