数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究带解题示例的电源变换
一个实际电压源由一个理想电压源串联一个内阻组成（对于理想电压源，该内阻为零，因此输出电压变得与负载电流无关）。而一个实际电流源由一个理想电流源并联一个内阻组成（对于理想电流源，该并联电阻为无穷大）。
实际电压源和电流源是可以相互转换的，即实际电压源可以转换为实际电流源，反之亦然。
电压源到电流源的转换
考虑一个电压为 V伏特，串联内阻为 Rint欧姆的实际电压源。负载电阻 RL欧姆连接在负载端子上。
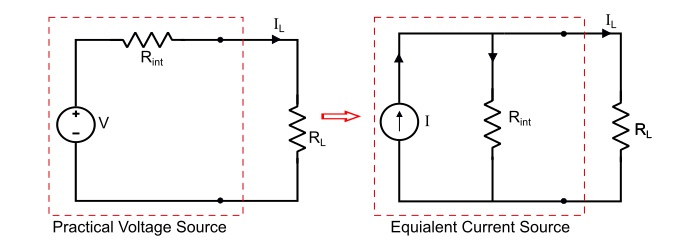
因此，参考实际电压源的电路，负载电流为
$$\mathrm{\mathit{I}_{L}=\frac{\mathit{V}}{\mathit{R}_{int}+ \mathit{R}_{L}}=\frac{\mathit{V} \mathit{R}_{int}}{(\mathit{R}_{int}+\mathit{R}_{L})\mathit{R}_{int}}=\frac{\mathit{V}}{\mathit{R}_{int}}(\frac{\mathit{R}_{int}}{\mathit{R}_{int}+\mathit{R}_{L}})}\:\:\:…(1)$$
现在，参考电流源的等效电路，负载电流为
$$\mathrm{\mathit{I}_{L}=\mathit{I}(\frac{\mathit{R}_{int}}{\mathit{R}_{int}+ \mathit{R}_{L}})}\:\:\:…(2)$$
为了使两个源相同，公式 (1) 和 (2) 应该产生相同的结果，即
$$\mathrm{\frac{\mathit{V}}{\mathit{R}_{int}}(\frac {\mathit{R}_{int}}{\mathit{R}_{int}+ \mathit{R}_{L}})=\mathit{I}(\frac {\mathit{R}_{int}}{\mathit{R}_{int}+ \mathit{R}_{L}})}$$
$$\mathrm{\Rightarrow\:\mathit{I}=\frac{\mathit{V}}{\mathit{R}_{int}}}\:\:\:…(3)$$
因此，一个恒定电压为 V，内阻为 Rint 的实际电压源等效于一个电流为 I = V/Rint，内阻为 Rint 的电流源，该内阻与电流源并联。
这里，等效电流源的内阻与电压源的内阻具有相同的值。
电流源到电压源的转换
考虑一个恒定电流为 I 安培，并联内阻为 Rint 的实际电流源，它可以转换为等效电压源，如下所示。
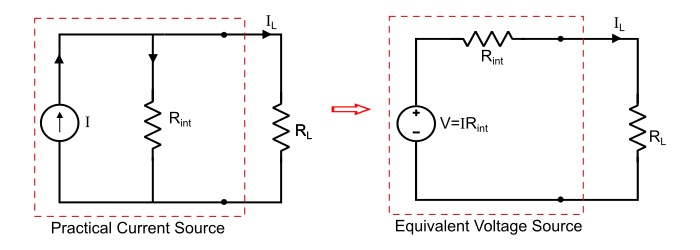
参考电流源的电路，负载电流为
$$\mathrm{\mathit{I}_{L}=\mathit{I}(\frac{\mathit{R}_{int}}{\mathit{R}_{int}+\mathit{R}_{L}})}\:\:\:… (4)$$
参考电压源的等效电路，负载电流为
$$\mathrm{\mathit{I}_{L}=\frac{\mathit{V}}{\mathit{R}_{int}+\mathit{R}_{L}}=\frac{V/\mathit{R}_{int}}{(\mathit{R}_{int}+\mathit{R}_{L})/\mathit{R}_{int}}=\frac{V}{\mathit{R}_{int}}(\frac{\mathit{R}_{int}}{\mathit{R}_{int}+\mathit{R}_{L}})}\:\:\:…(5)$$
为了使两个源相同，
$$\mathrm{\frac{\mathit{V}}{\mathit{R}_{int}}(\frac {\mathit{R}_{int}}{\mathit{R}_{int}+\mathit{R}_{L}})=I(\frac {\mathit{R}_{int}}{\mathit{R}_{int}+\mathit{R}_{L}})}$$
$$\mathrm{\Rightarrow\:\mathit{i}=\frac{\mathit{v}}{\mathit{R}_{int}}}$$
$$\mathrm{\Rightarrow\:\mathit{v}=\mathit{I}{\mathit{R}_{int}}}\:\:\:… (6)$$
因此，电流源可以转换为等效电压源，其中等效电压源的电压值为 V = IRint，电压源的串联电阻 Rint 与电流源的并联电阻具有相同的值。
数值示例 - 1
将一个串联内阻为 2 Ω 的 24 V 电压源转换为等效电流源。
解答
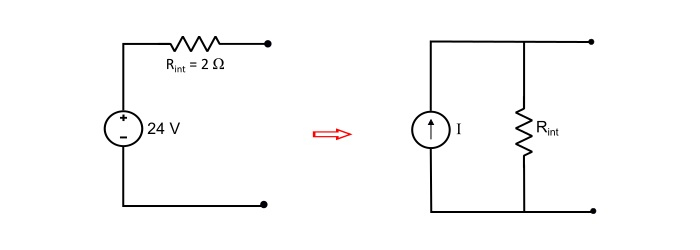
这里，等效电流源的源电流为
$$\mathrm{\mathit{I}=\frac{\mathit{V}}{\mathit{R}_{int}}=\frac{24}{2}=12\:A}$$
等效电流源的内阻 Rint 与原始电压源的值相同，因此
$$\mathrm{\mathit{R}_{int}=2\:Ω}$$
数值示例 - 2
一个电池的内阻为 2 Ω，开路电压为 24 V。当一个 6 Ω 的负载电阻连接到电池端子时，电池内部损耗的功率和端电压是多少？
解答
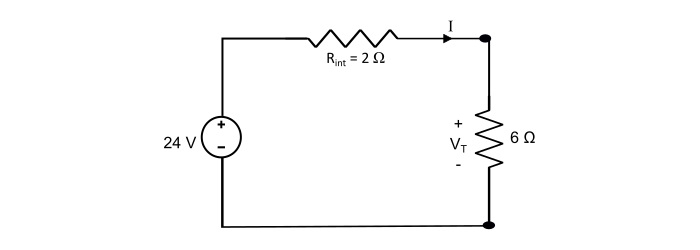
总电路电流为
$$\mathrm{\mathit{I}=\frac{24}{2+6}=3\:A}$$
$$\mathrm{电池内部损耗功率=\mathit{I}^{2}\mathit{R}_{int}=3^{2}×2=18\:W}$$
$$\mathrm{端电压(\mathit{V}_{r})=\mathit{IR}_{L}=3×6=18\:V}$$
23K+ 浏览量
