数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究C++实现完全二叉树中序遍历镜像节点之和
在这个问题中，我们得到一棵完全二叉树。我们的任务是创建一个程序来查找完全二叉树中镜像节点的中序遍历之和。
在这里，我们必须找到左子树的中序遍历，然后为每个节点添加其镜像节点的值。这意味着如果我们正在遍历左叶子节点，我们将把右叶子节点的值加到它上面，因为它就是镜像节点。
一些重要的定义
完全二叉树是二叉树，其中除最后一层外，所有层都具有最大数量的节点。
中序遍历是一种树遍历技术，其中首先访问左子树，然后访问根节点，最后访问右子树。
让我们举个例子来理解这个问题：
输入
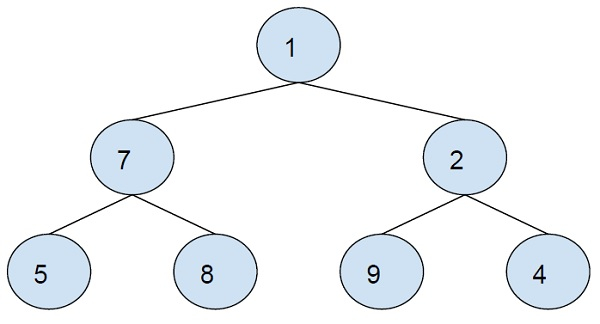
输出 − 9 9 17 2
解释 − 左子树的中序遍历是 5-7-8-1。
将所有节点与其镜像节点的值相加。
5 + 4 = 9 7 + 2 = 9 8 + 9 = 17 1 + 1 = 2
为了解决这个问题，我们将使用中序遍历来遍历二叉树。我们将使用两个节点，一个用于遍历左子树，另一个用于访问节点的镜像。例如，我们有左子树的根节点，我们将有一个镜像根节点来遍历它的镜像。
示例
程序演示解决方案的工作原理：
#include <iostream>
using namespace std;
typedef struct node {
int data;
struct node* left;
struct node* right;
node(int d){
data = d;
left = NULL;
right = NULL;
}
} Node;
void printMirrorSum(Node* root, Node* rootMirror){
if (root->left == NULL && rootMirror->right == NULL)
return;
printMirrorSum(root->left, rootMirror->right);
cout<<(root->left->data + rootMirror->right->data)<<endl;
printMirrorSum(root->right, rootMirror->left);
}
int main(){
Node* root = new Node(1);
root->left = new Node(7);
root->right = new Node(2);
root->left->left = new Node(5);
root->left->right = new Node(8);
root->right->left = new Node(9);
root->right->right = new Node(4);
cout<<"Sum of node and mirror image nodes are :\n";
printMirrorSum(root, root);
if (root)
cout<<(root->data + root->data);
return 0;
}输出
Sum of node and mirror image nodes are : 9 9 17 2
更新于: 2020年8月6日
浏览量 131
广告