树遍历

Table of content
上一页
下一页

遍历是访问树中所有节点的过程，也可能打印它们的的值。因为所有节点都通过边（链接）连接，我们总是从根（头部）节点开始。也就是说，我们无法随机访问树中的节点。有三种方法用于遍历树：

  • 中序遍历

  • 先序遍历

  • 后序遍历

通常，我们遍历树是为了搜索或定位树中给定的项或键，或者打印它包含的所有值。

中序遍历

在这种遍历方法中，先访问左子树，然后访问根节点，最后访问右子树。我们应该始终记住，每个节点本身都可以表示一个子树。

如果二叉树以**中序**方式遍历，则输出将以升序产生排序的键值。

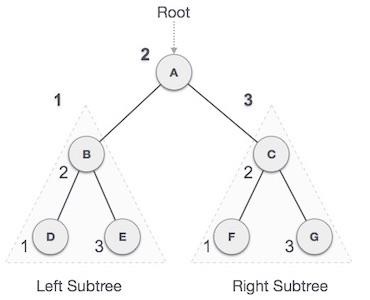
In-order Traversal

我们从**A**开始，按照中序遍历，移动到它的左子树**B**。**B**也以中序方式遍历。这个过程一直持续到所有节点都被访问。此树的中序遍历输出将为：

D → B → E → A → F → C → G

算法

直到所有节点都被遍历：

Step 1 − Recursively traverse left subtree.
Step 2 − Visit root node.
Step 3 − Recursively traverse right subtree.

示例

以下是此操作在各种编程语言中的实现：

C C++ Java Python
#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void inorder_traversal(struct node* root){
   if(root != NULL) {
      inorder_traversal(root->leftChild);
      printf("%d ",root->data);
      inorder_traversal(root->rightChild);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("Inorder traversal: ");
   inorder_traversal(root);
   return 0;
}

输出

Inorder traversal: 10 14 19 27 31 35 42

#include <iostream>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void inorder_traversal(struct node* root){
   if(root != NULL) {
      inorder_traversal(root->leftChild);
      printf("%d ",root->data);
      inorder_traversal(root->rightChild);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("Inorder traversal: ");
   inorder_traversal(root);
   return 0;
}

输出

Inorder traversal: 10 14 19 27 31 35 42 

class Node {
   int data;
   Node leftChild;
   Node rightChild;
   public Node(int key) {
      data = key;
      leftChild = rightChild = null;
   }
}
public class TreeDataStructure {
   Node root = null;
   void inorder_traversal(Node node) {
      if(node != null) {
         inorder_traversal(node.leftChild);
         System.out.print(node.data + " ");
         inorder_traversal(node.rightChild);
      }
   }
   public static void main(String args[]) {
      TreeDataStructure tree = new TreeDataStructure();
      tree.root = new Node(27);
      tree.root.leftChild = new Node(12);
      tree.root.rightChild = new Node(3);
      tree.root.leftChild.leftChild = new Node(44);
      tree.root.leftChild.rightChild = new Node(17);
      tree.root.rightChild.leftChild = new Node(56);
      System.out.println("Inorder traversal: ");
      tree.inorder_traversal(tree.root);
   }
}

输出

Inorder traversal: 
44 12 17 27 56 3 

class Node:
   def __init__(self, key):
      self.leftChild = None
      self.rightChild = None
      self.data = key

# Create a function to perform inorder tree traversal
def InorderTraversal(root):
   if root:
      InorderTraversal(root.leftChild)
      print(root.data)
      InorderTraversal(root.rightChild)

# Main class
if __name__ == "__main__":
   root = Node(3)
   root.leftChild = Node(26)
   root.rightChild = Node(42)
   root.leftChild.leftChild = Node(54)
   root.leftChild.rightChild = Node(65)
   root.rightChild.leftChild = Node(12)

   # Function call
   print("Inorder traversal of binary tree is")
   InorderTraversal(root)

输出

Inorder traversal of binary tree is
54
26
65
3
12
42

先序遍历

在这种遍历方法中，先访问根节点，然后访问左子树，最后访问右子树。

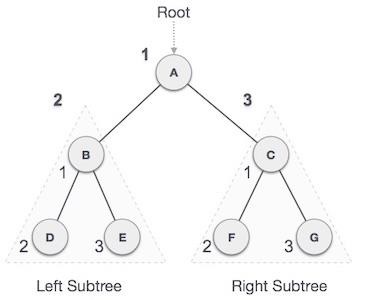
Pre-order Traversal

我们从**A**开始，按照先序遍历，首先访问**A**本身，然后移动到它的左子树**B**。**B**也以先序方式遍历。这个过程一直持续到所有节点都被访问。此树的先序遍历输出将为：

A → B → D → E → C → F → G

算法

直到所有节点都被遍历：

Step 1 − Visit root node.
Step 2 − Recursively traverse left subtree.
Step 3 − Recursively traverse right subtree.

示例

以下是此操作在各种编程语言中的实现：

C C++ Java Python
#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void pre_order_traversal(struct node* root){
   if(root != NULL) {
      printf("%d ",root->data);
      pre_order_traversal(root->leftChild);
      pre_order_traversal(root->rightChild);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("Preorder traversal: ");
   pre_order_traversal(root);
   return 0;
}

输出

Preorder traversal: 27 14 10 19 35 31 42 

#include <iostream>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void pre_order_traversal(struct node* root){
   if(root != NULL) {
      printf("%d ",root->data);
      pre_order_traversal(root->leftChild);
      pre_order_traversal(root->rightChild);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("Preorder traversal: ");
   pre_order_traversal(root);
   return 0;
}

输出

Preorder traversal: 27 14 10 19 35 31 42 

class Node {
   int data;
   Node leftChild;
   Node rightChild;
   public Node(int key) {
      data = key;
      leftChild = rightChild = null;
   }
}
public class TreeDataStructure {
   Node root = null;
   void pre_order_traversal(Node node) {
      if(node != null) {
         System.out.print(node.data + " ");
         pre_order_traversal(node.leftChild);
         pre_order_traversal(node.rightChild);
      }
   }
   public static void main(String args[]) {
      TreeDataStructure tree = new TreeDataStructure();
      tree.root = new Node(27);
      tree.root.leftChild = new Node(12);
      tree.root.rightChild = new Node(3);
      tree.root.leftChild.leftChild = new Node(44);
      tree.root.leftChild.rightChild = new Node(17);
      tree.root.rightChild.leftChild = new Node(56);
      System.out.println("Preorder traversal: ");
      tree.pre_order_traversal(tree.root);
   }
}

输出

Preorder traversal: 
27 12 44 17 3 56 

class Node:
   def __init__(self, key):
      self.leftChild = None
      self.rightChild = None
      self.data = key

# Create a function to perform postorder tree traversal
def PreorderTraversal(root):
   if root:
      print(root.data)
      PreorderTraversal(root.leftChild)
      PreorderTraversal(root.rightChild)

# Main class
if __name__ == "__main__":
   root = Node(3)
   root.leftChild = Node(26)
   root.rightChild = Node(42)
   root.leftChild.leftChild = Node(54)
   root.leftChild.rightChild = Node(65)
   root.rightChild.leftChild = Node(12)
   print("Preorder traversal of binary tree is")
   PreorderTraversal(root)

输出

Preorder traversal of binary tree is
3
26
54
65
42
12

后序遍历

在这种遍历方法中，根节点最后被访问，因此得名。首先遍历左子树，然后遍历右子树，最后遍历根节点。

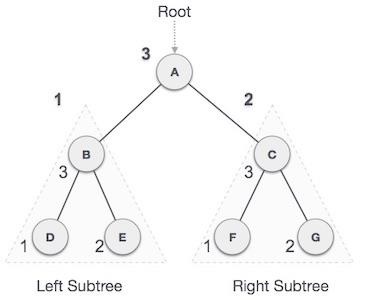
Post-order Traversal

我们从**A**开始，按照先序遍历，首先访问左子树**B**。**B**也以后序方式遍历。这个过程一直持续到所有节点都被访问。此树的后序遍历输出将为：

D → E → B → F → G → C → A

算法

直到所有节点都被遍历：

Step 1 − Recursively traverse left subtree.
Step 2 − Recursively traverse right subtree.
Step 3 − Visit root node.

示例

以下是此操作在各种编程语言中的实现：

C C++ Java Python
#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void post_order_traversal(struct node* root){
   if(root != NULL) {
      post_order_traversal(root->leftChild);
      post_order_traversal(root->rightChild);
      printf("%d ", root->data);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("Post order traversal: ");
   post_order_traversal(root);
   return 0;
}

输出

Post order traversal: 10 19 14 31 42 35 27

#include <iostream>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void post_order_traversal(struct node* root){
   if(root != NULL) {
      post_order_traversal(root->leftChild);
      post_order_traversal(root->rightChild);
      printf("%d ", root->data);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("Post order traversal: ");
   post_order_traversal(root);
   return 0;
}

输出

Post order traversal: 10 19 14 31 42 35 27

class Node {
   int data;
   Node leftChild;
   Node rightChild;
   public Node(int key) {
      data = key;
      leftChild = rightChild = null;
   }
}
public class TreeDataStructure {
   Node root = null;
   void post_order_traversal(Node node) {
      if(node != null) {
         post_order_traversal(node.leftChild);
         post_order_traversal(node.rightChild);
         System.out.print(node.data + " ");
      }
   }
   public static void main(String args[]) {
      TreeDataStructure tree = new TreeDataStructure();
      tree.root = new Node(27);
      tree.root.leftChild = new Node(12);
      tree.root.rightChild = new Node(3);
      tree.root.leftChild.leftChild = new Node(44);
      tree.root.leftChild.rightChild = new Node(17);
      tree.root.rightChild.leftChild = new Node(56);
      System.out.println("Post order traversal: ");
      tree.post_order_traversal(tree.root);
   }
}

输出

Post order traversal: 
44 17 12 56 3 27 

class Node:
   def __init__(self, key):
      self.leftChild = None
      self.rightChild = None
      self.data = key

# Create a function to perform preorder tree traversal
def PostorderTraversal(root):
   if root:
      PostorderTraversal(root.leftChild)
      PostorderTraversal(root.rightChild)
      print(root.data)

# Main class
if __name__ == "__main__":
   root = Node(3)
   root.leftChild = Node(26)
   root.rightChild = Node(42)
   root.leftChild.leftChild = Node(54)
   root.leftChild.rightChild = Node(65)
   root.rightChild.leftChild = Node(12)
   print("Postorder traversal of binary tree is")
   PostorderTraversal(root)

输出

Postorder traversal of binary tree is
54
65
26
12
42
3

完整实现

现在让我们看看树遍历在各种编程语言中的完整实现：

C C++ Java Python
#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

//if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void pre_order_traversal(struct node* root){
   if(root != NULL) {
      printf("%d ",root->data);
      pre_order_traversal(root->leftChild);
      pre_order_traversal(root->rightChild);
   }
}
void inorder_traversal(struct node* root){
   if(root != NULL) {
      inorder_traversal(root->leftChild);
      printf("%d ",root->data);
      inorder_traversal(root->rightChild);
   }
}
void post_order_traversal(struct node* root){
   if(root != NULL) {
      post_order_traversal(root->leftChild);
      post_order_traversal(root->rightChild);
      printf("%d ", root->data);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("Preorder traversal: ");
   pre_order_traversal(root);
   printf("\nInorder traversal: ");
   inorder_traversal(root);
   printf("\nPost order traversal: ");
   post_order_traversal(root);
   return 0;
}

输出

Preorder traversal: 27 14 10 19 35 31 42 
Inorder traversal: 10 14 19 27 31 35 42 
Post order traversal: 10 19 14 31 42 35 27

#include <iostream>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void pre_order_traversal(struct node* root){
   if(root != NULL) {
      printf("%d ",root->data);
      pre_order_traversal(root->leftChild);
      pre_order_traversal(root->rightChild);
   }
}
void inorder_traversal(struct node* root){
   if(root != NULL) {
      inorder_traversal(root->leftChild);
      printf("%d ",root->data);
      inorder_traversal(root->rightChild);
   }
}
void post_order_traversal(struct node* root){
   if(root != NULL) {
      post_order_traversal(root->leftChild);
      post_order_traversal(root->rightChild);
      printf("%d ", root->data);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("Preorder traversal: ");
   pre_order_traversal(root);
   printf("\nInorder traversal: ");
   inorder_traversal(root);
   printf("\nPost order traversal: ");
   post_order_traversal(root);
   return 0;
}

输出

Preorder traversal: 27 14 10 19 35 31 42 
Inorder traversal: 10 14 19 27 31 35 42 
Post order traversal: 10 19 14 31 42 35 27 

class Node {
   int data;
   Node leftChild;
   Node rightChild;
   public Node(int key) {
      data = key;
      leftChild = rightChild = null;
   }
}
public class TreeDataStructure {
   Node root = null;
   void inorder_traversal(Node node) {
      if(node != null) {
         inorder_traversal(node.leftChild);
         System.out.print(node.data + " ");
         inorder_traversal(node.rightChild);
      }
   }
   void pre_order_traversal(Node node) {
      if(node != null) {
         System.out.print(node.data + " ");
         pre_order_traversal(node.leftChild);
         pre_order_traversal(node.rightChild);
      }
   }
   void post_order_traversal(Node node) {
      if(node != null) {
         post_order_traversal(node.leftChild);
         post_order_traversal(node.rightChild);
         System.out.print(node.data + " ");
      }
   }
   public static void main(String args[]) {
      TreeDataStructure tree = new TreeDataStructure();
      tree.root = new Node(27);
      tree.root.leftChild = new Node(12);
      tree.root.rightChild = new Node(3);
      tree.root.leftChild.leftChild = new Node(44);
      tree.root.leftChild.rightChild = new Node(17);
      tree.root.rightChild.leftChild = new Node(56);
      System.out.println("Inorder traversal: ");
      tree.inorder_traversal(tree.root);
      System.out.println("\nPreorder traversal: ");
      tree.pre_order_traversal(tree.root);
      System.out.println("\nPost order traversal: ");
      tree.post_order_traversal(tree.root);
   }
}

输出

Inorder traversal: 
44 12 17 27 56 3 
Preorder traversal: 
27 12 44 17 3 56 
Post order traversal: 
44 17 12 56 3 27 

class Node:
   def __init__(self, key):
      self.leftChild = None
      self.rightChild = None
      self.data = key

# Create a function to perform inorder tree traversal
def InorderTraversal(root):
   if root:
      InorderTraversal(root.leftChild)
      print(root.data)
      InorderTraversal(root.rightChild)

# Create a function to perform preorder tree traversal
def PostorderTraversal(root):
   if root:
      PostorderTraversal(root.leftChild)
      PostorderTraversal(root.rightChild)
      print(root.data)

# Create a function to perform postorder tree traversal
def PreorderTraversal(root):
   if root:
      print(root.data)
      PreorderTraversal(root.leftChild)
      PreorderTraversal(root.rightChild)

# Main class
if __name__ == "__main__":
   root = Node(3)
   root.leftChild = Node(26)
   root.rightChild = Node(42)
   root.leftChild.leftChild = Node(54)
   root.leftChild.rightChild = Node(65)
   root.rightChild.leftChild = Node(12)

   # Function call
   print("Inorder traversal of binary tree is")
   InorderTraversal(root)
   print("\nPreorder traversal of binary tree is")
   PreorderTraversal(root)
   print("\nPostorder traversal of binary tree is")
   PostorderTraversal(root)

输出

Inorder traversal of binary tree is
54
26
65
3
12
42

Preorder traversal of binary tree is
3
26
54
65
42
12

Postorder traversal of binary tree is
54
65
26
12
42
3
打印页面
上一页
下一页
广告