生成树

什么是生成树？

生成树是图G的一个子集，它包含所有顶点，并且边数最少。因此，生成树不包含环路，并且不能是断开的。

根据这个定义，我们可以得出结论，每个连通且无向的图G至少有一棵生成树。断开的图没有任何生成树，因为它无法扩展到所有顶点。

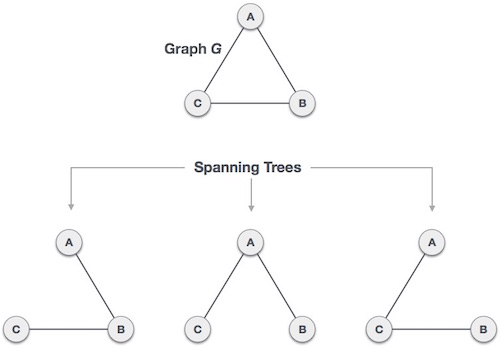
我们找到了一个完整图的三个生成树。一个完整的无向图最多可以有n^n-2个生成树，其中n是节点数。在上面提到的例子中，n是3，因此可以有3³⁻² = 3个生成树。

生成树的一般属性

现在我们了解了一个图可以有多个生成树。以下是与图G相关的生成树的一些属性：

• 一个连通图G可以有多个生成树。

• 图G的所有可能的生成树具有相同数量的边和顶点。

• 生成树不包含任何环路（回路）。

• 从生成树中移除一条边将使图断开，即生成树是最小连通的。

• 向生成树中添加一条边将创建一个回路或环路，即生成树是最大无环的。

生成树的数学性质

• 生成树有n-1条边，其中n是节点（顶点）的数量。

• 从一个完整图中，通过移除最多e - n + 1条边，我们可以构建一棵生成树。

• 一个完整图最多可以有n^n-2个生成树。

因此，我们可以得出结论，生成树是连通图G的一个子集，而断开的图没有生成树。

生成树的应用

生成树主要用于找到连接图中所有节点的最小路径。生成树的常见应用包括：

• 民用网络规划

• 计算机网络路由协议

• 聚类分析

让我们通过一个简单的例子来理解这一点。假设城市网络是一个巨大的图，现在计划以最少的线路部署电话线路，以便连接到所有城市节点。这就是生成树发挥作用的地方。

最小生成树 (MST)

在带权图中，最小生成树是指权重小于同一图中所有其他生成树的生成树。在现实情况下，此权重可以测量为距离、拥塞、交通负载或分配给边的任何任意值。

最小生成树算法

我们将在本文中学习两种最重要的生成树算法：

• 克鲁斯卡尔算法

• 普里姆算法

这两种算法都是贪心算法。