数组数据结构

上一页
下一页

什么是数组？

数组是一种线性数据结构，定义为一组具有相同或不同数据类型的元素的集合。它们存在于单维度和多维度中。当需要将多个类似性质的元素存储在一个地方时，这些数据结构就会出现。

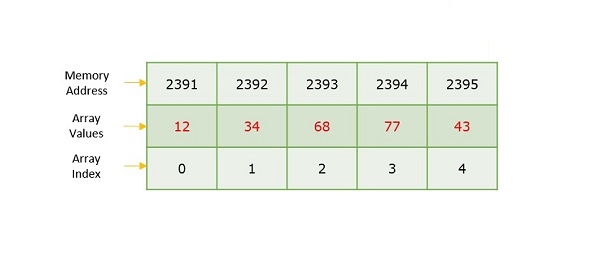
Array

数组索引和内存地址的区别在于，数组索引充当标记数组中元素的键值。但是，内存地址是可用空闲内存的起始地址。

以下是了解数组概念的重要术语。

  • 元素 - 存储在数组中的每个项目都称为元素。

  • 索引 - 数组中每个元素的位置都有一个数字索引，用于识别该元素。

语法

在C和C++编程语言中创建数组 -

data_type array_name[array_size]={elements separated by commas}
or,
data_type array_name[array_size];

在Java编程语言中创建数组 -

data_type[] array_name = {elements separated by commas}
or,
data_type array_name = new data_type[array_size];

数组的必要性

数组被用作从小型排序问题到更复杂问题（如旅行推销员问题）的许多问题的解决方案。除了数组之外，还有许多其他数据结构为这些问题提供了高效的时间和空间复杂度，那么是什么使使用数组变得更好呢？答案在于随机访问查找时间。

数组提供O(1)随机访问查找时间。这意味着访问数组的第1个索引和数组的第1000个索引将花费相同的时间。这是因为数组带有一个指针和一个偏移量值。指针指向内存的正确位置，偏移量值显示在所述内存中查找多远。

                           array_name[index]
                              |       |
                           Pointer   Offset

因此，在一个包含6个元素的数组中，要访问第一个元素，数组将指向第0个索引。类似地，要访问第6个元素，数组将指向第5个索引。

数组表示

数组表示为一组桶，每个桶存储一个元素。这些桶从'0'到'n-1'索引，其中n是该特定数组的大小。例如，大小为10的数组将具有从0到9索引的桶。

此索引对于多维数组也将类似。如果它是二维数组，则每个桶中将有子桶。然后它将被索引为array_name[m][n]，其中m和n是数组中每个级别的尺寸。

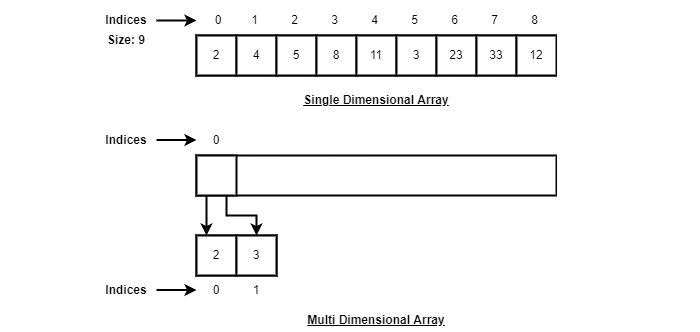
Array Representation

根据以上说明，以下是要考虑的重要事项。

  • 索引从0开始。

  • 数组长度为9，这意味着它可以存储9个元素。

  • 每个元素都可以通过其索引访问。例如，我们可以获取索引为6的元素作为23。

数组的基本操作

数组的基本操作包括插入、删除、搜索、显示、遍历和更新。这些操作通常用于修改数组中的数据或报告数组的状态。

以下是数组支持的基本操作。

  • 遍历 - 一次打印所有数组元素。

  • 插入 - 在给定索引处添加一个元素。

  • 删除 - 删除给定索引处的元素。

  • 搜索 - 使用给定索引或值搜索元素。

  • 更新 - 更新给定索引处的元素。

  • 显示 - 显示数组的内容。

在C中，当数组初始化为指定大小后，它会按照以下顺序为其元素分配默认值。

数据类型 默认值
bool false
char 0
int 0
float 0.0
double 0.0f
void
wchar_t 0

数组 - 插入操作

在插入操作中，我们将一个或多个元素添加到数组中。根据需要，可以在数组的开头、结尾或任何给定索引处添加新元素。这是使用编程语言的输入语句完成的。

算法

以下是在线性数组中插入元素的算法，直到我们到达数组的末尾 -

1. Start
2. Create an Array of a desired datatype and size.
3. Initialize a variable 'i' as 0.
4. Enter the element at ith index of the array.
5. Increment i by 1.
6. Repeat Steps 4 & 5 until the end of the array.
7. Stop

示例

在这里，我们看到了插入操作的实际实现，我们将在数组末尾添加数据 -

C C++ Java Python
#include <stdio.h>
int main(){
   int LA[3] = {}, i;
   printf("Array Before Insertion:\n");
   for(i = 0; i < 3; i++)
      printf("LA[%d] = %d \n", i, LA[i]);
   printf("Inserting Elements.. \n");
   printf("The array elements after insertion :\n"); // prints array values
   for(i = 0; i < 3; i++) {
      LA[i] = i + 2;
      printf("LA[%d] = %d \n", i, LA[i]);
   }
   return 0;
}

#include <iostream>
using namespace std;
int main(){
   int LA[3] = {}, i;
   cout << "Array Before Insertion:" << endl;
   for(i = 0; i < 3; i++)
      cout << "LA[" << i <<"] = " << LA[i] << endl; 
      
   //prints garbage values
   cout << "Inserting elements.." <<endl;
   cout << "Array After Insertion:" << endl; // prints array values
   for(i = 0; i < 5; i++) {
      LA[i] = i + 2;
      cout << "LA[" << i <<"] = " << LA[i] << endl;
   }
   return 0;
}

public class ArrayDemo {
   public static void main(String []args) {
      int LA[] = new int[3];
      System.out.println("Array Before Insertion:");
      for(int i = 0; i < 3; i++)
         System.out.println("LA[" + i + "] = " + LA[i]); //prints empty array
      System.out.println("Inserting Elements..");
      
      // Printing Array after Insertion
      System.out.println("Array After Insertion:");
      for(int i = 0; i < 3; i++) {
         LA[i] = i+3;
         System.out.println("LA[" + i + "] = " + LA[i]);
      }
   }
}

# python program to insert element using insert operation
def insert(arr, element):
	arr.append(element)
# Driver's code
if __name__ == '__main__':
	# declaring array and value to insert
	LA = [0, 0, 0]
	x = 0
	# array before inserting an element
	print("Array Before Insertion: ")
	for x in range(len(LA)):
	    print("LA", [x], " = " , LA[x])
	print("Inserting elements....")
	# array after Inserting element
	for x in range(len(LA)):
	    LA.append(x);
	    LA[x] = x+1;
	print("Array After Insertion: ")
	for x in range(len(LA)):
	    print("LA", [x], " = " , LA[x])

输出

Array Before Insertion:
LA[0] = 0
LA[1] = 0
LA[2] = 0
Inserting elements..
Array After Insertion:
LA[0] = 2
LA[1] = 3
LA[2] = 4
LA[3] = 5
LA[4] = 6

对于数组插入操作的其他变体，点击此处。

数组 - 删除操作

在此数组操作中，我们从数组的特定索引中删除一个元素。此删除操作发生在我们为后续索引中的值分配给当前索引时。

算法

假设LA是一个包含N个元素的线性数组，K是一个正整数，使得K<=N。以下是删除LA中第K个位置的元素的算法。

1. Start
2. Set J = K
3. Repeat steps 4 and 5 while J < N
4. Set LA[J] = LA[J + 1]
5. Set J = J+1
6. Set N = N-1
7. Stop

示例

以下是此操作在各种编程语言中的实现 -

C C++ Java Python
#include <stdio.h>
void main(){
   int LA[] = {1,3,5};
   int n = 3;
   int i;
   printf("The original array elements are :\n");
   for(i = 0; i<n; i++)
      printf("LA[%d] = %d \n", i, LA[i]);
   for(i = 1; i<n; i++) {
      LA[i] = LA[i+1];
      n = n - 1;
   }
   printf("The array elements after deletion :\n");
   for(i = 0; i<n; i++)
      printf("LA[%d] = %d \n", i, LA[i]);
}

#include <iostream>
using namespace std;
int main(){
   int LA[] = {1,3,5};
   int i, n = 3;
   cout << "The original array elements are :"<<endl;
   for(i = 0; i<n; i++) {
      cout << "LA[" << i << "] = " << LA[i] << endl;
   }
   for(i = 1; i<n; i++) {
      LA[i] = LA[i+1];
      n = n - 1;
   }
   cout << "The array elements after deletion :"<<endl;
   for(i = 0; i<n; i++) {
      cout << "LA[" << i << "] = " << LA[i] <<endl;
   }
}

public class ArrayDemo {
   public static void main(String []args) {
      int LA[] = new int[3];
      int n = LA.length;
      System.out.println("Array Before Deletion:");
      for(int i = 0; i < n; i++) {
         LA[i] = i + 3;
         System.out.println("LA[" + i + "] = " + LA[i]);
      }
      for(int i = 1; i<n-1; i++) {
         LA[i] = LA[i+1];
         n = n - 1;
      }
      System.out.println("Array After Deletion:");
      for(int i = 0; i < n; i++) {
         System.out.println("LA[" + i + "] = " + LA[i]);
      }
   }
}

#python program to delete the value using delete operation
if __name__ == '__main__':
	# Declaring array and deleting value
	LA = [0,0,0]
	n = len(LA)
	print("Array Before Deletion: ")
	for x in range(len(LA)):
	    LA.append(x)
	    LA[x] = x + 3
	    print("LA", [x], " = " , LA[x])
	# delete the value if exists 
	# or show error it does not exist in the list 
	for x in range(1, n-1):
	    LA[x] = LA[x+1]
	    n = n-1
	print("Array After Deletion: ")
	for x in range(n):
	    print("LA", [x], " = " , LA[x])

输出

The original array elements are :
LA[0] = 1
LA[1] = 3
LA[2] = 5
The array elements after deletion :
LA[0] = 1
LA[1] = 5

数组 - 搜索操作

使用键在数组中搜索元素；键元素依次比较数组中的每个值，以检查键是否存在于数组中。

算法

假设LA是一个包含N个元素的线性数组，K是一个正整数，使得K<=N。以下是使用顺序搜索查找值为ITEM的元素的算法。

1. Start
2. Set J = 0
3. Repeat steps 4 and 5 while J < N
4. IF LA[J] is equal ITEM THEN GOTO STEP 6
5. Set J = J +1
6. PRINT J, ITEM
7. Stop

示例

以下是此操作在各种编程语言中的实现 -

C C++ Java Python
#include <stdio.h>
void main(){
   int LA[] = {1,3,5,7,8};
   int item = 5, n = 5;
   int i = 0, j = 0;
   printf("The original array elements are :\n");
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
   for(i = 0; i<n; i++) {
      if( LA[i] == item ) {
         printf("Found element %d at position %d\n", item, i+1);
      }
   }
}

#include <iostream>
using namespace std;
int main(){
   int LA[] = {1,3,5,7,8};
   int item = 5, n = 5;
   int i = 0;
   cout << "The original array elements are : " <<endl;
   for(i = 0; i<n; i++) {
      cout << "LA[" << i << "] = " << LA[i] << endl;
   }
   for(i = 0; i<n; i++) {
      if( LA[i] == item ) {
         cout << "Found element " << item << " at position " << i+1 <<endl;
      }
   }
   return 0;
}

public class ArrayDemo{
   public static void main(String []args){
      int LA[] = new int[5];
      System.out.println("Array:");
      for(int i = 0; i < 5; i++) {
         LA[i] = i + 3;
         System.out.println("LA[" + i + "] = " + LA[i]);
      }
      for(int i = 0; i < 5; i++) {
         if(LA[i] == 6)
            System.out.println("Element " + 6 + " is found at index " + i);
      }
   }
}

#search operation using python
def findElement(arr, n, value):
	for i in range(n):
		if (arr[i] == value):
			return i
	# If the key is not found
	return -1
# Driver's code
if __name__ == '__main__':
	LA = [1,3,5,7,8]
	print("Array element are: ")
	for x in range(len(LA)):
	    print("LA", [x], " = ", LA[x])
	value = 5
	n = len(LA)
		# element found using search operation
	index = findElement(LA, n, value)
	if index != -1:
		print("Element", value, "Found at position = " + str(index + 1))
	else:
		print("Element not found")

输出

The original array elements are :
LA[0] = 1
LA[1] = 3
LA[2] = 5
LA[3] = 7
LA[4] = 8
Found element 5 at position 3

数组 - 遍历操作

此操作遍历数组的所有元素。我们使用循环语句来执行此操作。

算法

以下是遍历线性数组中所有元素的算法 -

1  Start
2. Initialize an Array of certain size and datatype.
3. Initialize another variable ‘i’ with 0.
4. Print the ith value in the array and increment i.
5. Repeat Step 4 until the end of the array is reached.
6. End

示例

以下是此操作在各种编程语言中的实现 -

C C++ Java Python
#include <stdio.h>
int main(){
   int LA[] = {1,3,5,7,8};
   int item = 10, k = 3, n = 5;
   int i = 0, j = n;
   printf("The original array elements are :\n");
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

#include <iostream>
using namespace std;
int main(){
   int LA[] = {1,3,5,7,8};
   int item = 10, k = 3, n = 5;
   int i = 0, j = n;
   cout << "The original array elements are:\n";
   for(i = 0; i<n; i++)
      cout << "LA[" << i << "] = " << LA[i] << endl;
   return 0;
}

public class ArrayDemo {
   public static void main(String []args) {
      int LA[] = new int[5];
      System.out.println("The array elements are: ");
      for(int i = 0; i < 5; i++) {
         LA[i] = i + 2;
         System.out.println("LA[" + i + "] = " + LA[i]);
      }
   }
}

# Python code to iterate over a array using python
LA = [1, 3, 5, 7, 8]
# length of the elements
length = len(LA)
# Traversing the elements using For loop and range
# same as 'for x in range(len(array))'
print("Array elements are: ")
for x in range(length):
	print("LA", [x], " = ", LA[x])

输出

The original array elements are :
LA[0] = 1
LA[1] = 3
LA[2] = 5
LA[3] = 7
LA[4] = 8

数组 - 更新操作

更新操作是指更新数组中给定索引处的现有元素。

算法

假设LA是一个包含N个元素的线性数组，K是一个正整数，使得K<=N。以下是更新LA中第K个位置的元素的算法。

1. Start
2. Set LA[K-1] = ITEM
3. Stop

示例

以下是此操作在各种编程语言中的实现 -

C C++ Java Python
#include <stdio.h>
void main(){
   int LA[] = {1,3,5,7,8};
   int k = 3, n = 5, item = 10;
   int i, j;
   printf("The original array elements are :\n");
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
   LA[k-1] = item;
   printf("The array elements after updation :\n");
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

#include <iostream>
using namespace std;
int main(){
   int LA[] = {1,3,5,7,8};
   int item = 10, k = 3, n = 5;
   int i = 0, j = n;
   cout << "The original array elements are :\n";
   for(i = 0; i<n; i++)
      cout << "LA[" << i << "] = " << LA[i] << endl;
   LA[2] = item;
   cout << "The array elements after updation are :\n";
   for(i = 0; i<n; i++)
      cout << "LA[" << i << "] = " << LA[i] << endl;
   return 0;
}

public class ArrayDemo {
   public static void main(String []args) {
      int LA[] = new int[5];
      int item = 15;
      System.out.println("The array elements are: ");
      for(int i = 0; i < 5; i++) {
         LA[i] = i + 2;
         System.out.println("LA[" + i + "] = " + LA[i]);
      }
      LA[3] = item;
      System.out.println("The array elements after updation are: ");
      for(int i = 0; i < 5; i++)
         System.out.println("LA[" + i + "] = " + LA[i]);
   }
}

#update operation using python
#Declaring array elements
LA = [1,3,5,7,8]
#before updation
print("The original array elements are :");
for x in range(len(LA)):
    print("LA", [x], " = ", LA[x])
#after updation
LA[2] = 10
print("The array elements after updation are: ")
for x in range(len(LA)):
    print("LA", [x], " = ", LA[x])

输出

The original array elements are :
LA[0] = 1
LA[1] = 3
LA[2] = 5
LA[3] = 7
LA[4] = 8
The array elements after updation :
LA[0] = 1
LA[1] = 3
LA[2] = 10
LA[3] = 7
LA[4] = 8

数组 - 显示操作

此操作使用打印语句显示整个数组中的所有元素。

算法

假设LA是一个包含N个元素的线性数组。以下是显示数组元素的算法。

1. Start
2. Print all the elements in the Array
3. Stop

示例

以下是此操作在各种编程语言中的实现 -

C C++ Java Python
#include <stdio.h>
int main(){
   int LA[] = {1,3,5,7,8};
   int n = 5;
   int i;
   printf("The original array elements are :\n");
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

#include <iostream>
using namespace std;
int main(){
   int LA[] = {1,3,5,7,8};
   int n = 5;
   int i;
   cout << "The original array elements are :\n";
   for(i = 0; i<n; i++)
      cout << "LA[" << i << "] = " << LA[i] << endl;
   return 0;
}

public class ArrayDemo {
   public static void main(String []args) {
      int LA[] = new int[5];
      System.out.println("The array elements are: ");
      for(int i = 0; i < 5; i++) {
         LA[i] = i + 2;
         System.out.println("LA[" + i + "] = " + LA[i]);
      }
   }
}

#Display operation using python
#Display operation using python
#Declaring array elements
LA = [2,3,4,5,6]
#Displaying the array
print("The array elements are: ")
for x in range(len(LA)):
    print("LA", [x], " = " , LA[x])

输出

The original array elements are :
LA[0] = 1
LA[1] = 3
LA[2] = 5
LA[3] = 7
LA[4] = 8
打印页面

上一页
下一页
广告
© . All rights reserved.