希尔排序算法

希尔排序是一种高效的排序算法，它基于插入排序算法。该算法避免了插入排序中可能出现的大量位移，尤其是在较小值位于最右侧且需要移动到最左侧的情况。

该算法首先对间隔较大的元素进行插入排序，然后对间隔较小的元素进行排序。这个间隔被称为**步长**。步长的计算基于Knuth公式：

h = h * 3 + 1
where −
   h is interval with initial value 1

对于中等规模的数据集，该算法效率很高，其平均和最坏情况下的时间复杂度均为O(n)，其中**n**是元素个数。

希尔排序算法

以下是希尔排序算法：

1. Initialize the value of h.
2. Divide the list into smaller sub-list of equal interval h.
3. Sort these sub-lists using insertion sort.
4. Repeat until complete list is sorted.

伪代码

以下是希尔排序的伪代码：

procedure shellSort()
   A : array of items

   /* calculate interval*/
   while interval < A.length /3 do:
      interval = interval * 3 + 1
   end while

   while interval > 0 do:
      for outer = interval; outer < A.length; outer ++ do:

         /* select value to be inserted */
         valueToInsert = A[outer]
         inner = outer;
            
            /*shift element towards right*/
            while inner > interval -1 &&  A[inner - interval] 
			>= valueToInsert do:
               A[inner] = A[inner - interval]
               inner = inner – interval
            end while
         
         /* insert the number at hole position */
         A[inner] = valueToInsert
         end for
   
   /* calculate interval*/
   interval = (interval -1) /3;
   end while
end procedure

示例

让我们考虑以下示例，了解希尔排序的工作原理。我们使用前面示例中相同的数组。为了方便理解，我们将步长设为4。创建一个虚拟子列表，包含所有间隔为4位置的元素。这些元素为{35, 14}, {33, 19}, {42, 27}和{10, 14}

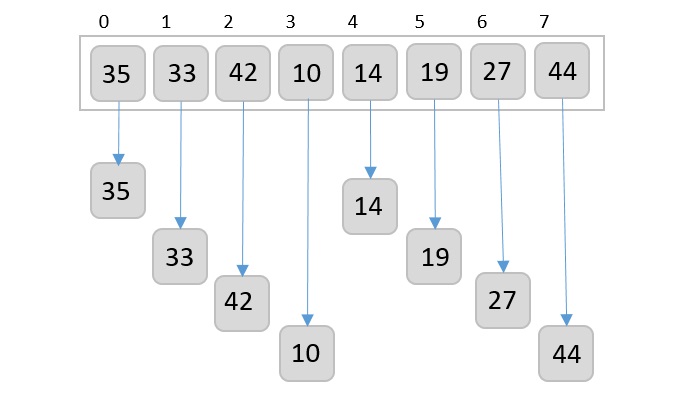
我们比较每个子列表中的元素，并在原数组中交换它们（如有必要）。此步骤后，新数组应如下所示：

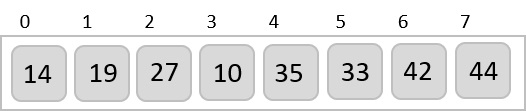
然后，我们将步长设为2，这将生成两个子列表 - {14, 27, 35, 42}, {19, 10, 33, 44}

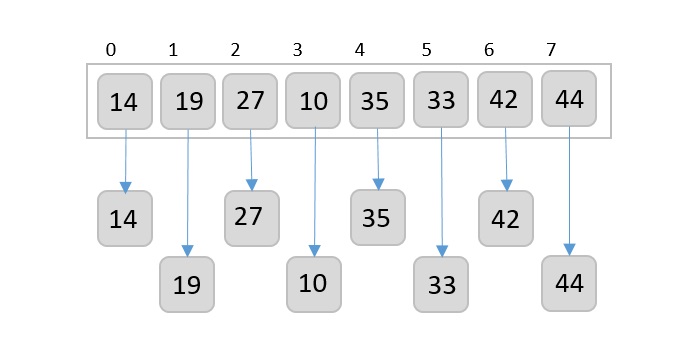
我们比较并交换原数组中需要的元素。此步骤后，数组应如下所示：

最后，我们使用步长为1的值对其余数组进行排序。希尔排序使用插入排序对数组进行排序。

以下是分步说明：

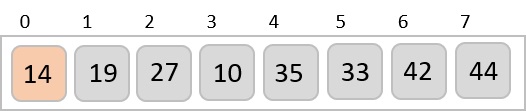
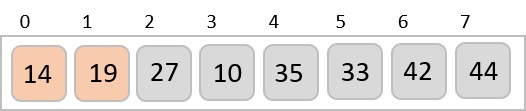
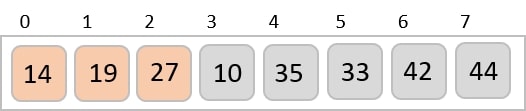
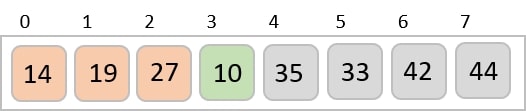
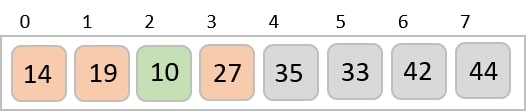
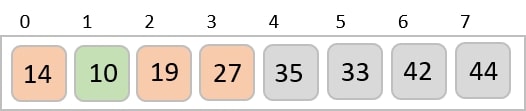
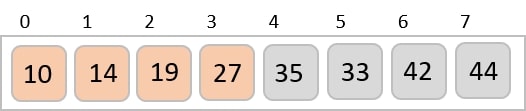
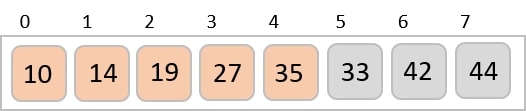
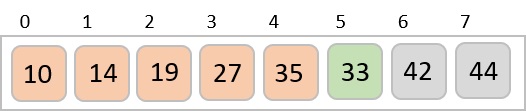
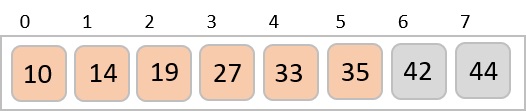
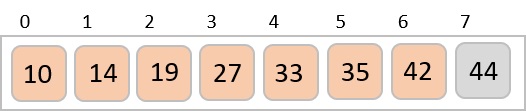
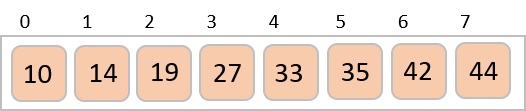
我们看到只需要四次交换就能对其余数组进行排序。

实现

希尔排序是一种高效的排序算法，它基于插入排序算法。该算法避免了插入排序中可能出现的大量位移，尤其是在较小值位于最右侧且需要移动到最左侧的情况。

#include <stdio.h>
void shellSort(int arr[], int n){
   int gap, j, k;
   for(gap = n/2; gap > 0; gap = gap / 2) { //initially gap = n/2, decreasing by gap /2
      for(j = gap; j<n; j++) {
         for(k = j-gap; k>=0; k -= gap) {
            if(arr[k+gap] >= arr[k])
               break;
            else {
               int temp;
               temp = arr[k+gap];
               arr[k+gap] = arr[k];
               arr[k] = temp;
            }
         }
      }
   }
}
int main(){
   int n;
   n = 5;
   int arr[5] = {33, 45, 62, 12, 98}; // initialize the array
   printf("Array before Sorting: ");
   for(int i = 0; i<n; i++)
      printf("%d ",arr[i]);
   printf("\n");
   shellSort(arr, n);
   printf("Array after Sorting: ");
   for(int i = 0; i<n; i++)
      printf("%d ", arr[i]);
   printf("\n");
}

Array before Sorting: 33 45 62 12 98
Array after Sorting: 12 33 45 62 98

#include<iostream>
using namespace std;
void shellSort(int *arr, int n){
   int gap, j, k;
   for(gap = n/2; gap > 0; gap = gap / 2) { //initially gap = n/2, decreasing by gap /2
      for(j = gap; j<n; j++) {
         for(k = j-gap; k>=0; k -= gap) {
            if(arr[k+gap] >= arr[k])
               break;
            else {
               int temp;
               temp = arr[k+gap];
               arr[k+gap] = arr[k];
               arr[k] = temp;
            }
         }
      }
   }
}
int main(){
   int n;
   n = 5;
   int arr[5] = {33, 45, 62, 12, 98}; // initialize the array
   cout << "Array before Sorting: ";
   for(int i = 0; i<n; i++)
      cout << arr[i] << " ";
   cout << endl;
   shellSort(arr, n);
   cout << "Array after Sorting: ";
   for(int i = 0; i<n; i++)
      cout << arr[i] << " ";
   cout << endl;
}

Array before Sorting: 33 45 62 12 98
Array after Sorting: 12 33 45 62 98

import java.io.*;
import java.util.*;
public class ShellSort {
   public static void main(String args[]) {
      int n = 5;
      int[] arr = {33, 45, 62, 12, 98}; //initialize an array
      System.out.print("Array before Sorting: ");
      for(int i = 0; i<n; i++)
         System.out.print(arr[i] + " ");
      System.out.println();
      int gap;
      for(gap = n/2; gap > 0; gap = gap / 2) { //initially gap = n/2, decreasing by gap /2
         for(int j = gap; j<n; j++) {
            for(int k = j-gap; k>=0; k -= gap) {
               if(arr[k+gap] >= arr[k])
                  break;
               else {
                  int temp;
                  temp = arr[k+gap];
                  arr[k+gap] = arr[k];
                  arr[k] = temp;
               }
            }
         }
      }
      System.out.print("Array After Sorting: ");
      for(int i = 0; i<n; i++)
         System.out.print(arr[i] + " ");
      System.out.println();
   }
}

Array before Sorting: 33 45 62 12 98
Array After Sorting: 12 33 45 62 98

def shell_sort(array,n):
   gap = n//2 #using floor division to avoid float values as result
   while gap > 0:
      for i in range(int(gap),n):
         temp = array[i]
         j = i
         while j >= gap and array[j-gap] >temp:
            array[j] = array[j-gap]
            j -= gap
            array[j] = temp
      gap = gap // 2 #using floor division to avoid float values as result

arr = [33, 45, 62, 12, 98]
n = len(arr)
print("Array before Sorting: ")
print(arr)
shell_sort(arr, n);
print("Array after Sorting: ")
print(arr)

Array before Sorting: 
[33, 45, 62, 12, 98]
Array after Sorting: 
[12, 33, 45, 62, 98]