递归算法

递归

许多计算机编程语言允许模块或函数调用自身。这种技术称为递归。在递归中，函数α要么直接调用自身，要么调用一个函数β，而该函数又反过来调用原始函数α。函数α称为递归函数。

示例 - 函数调用自身。

int function(int value) {
   if(value < 1)
      return;
   function(value - 1);

   printf("%d ",value);   
}

示例 - 一个函数调用另一个函数，而另一个函数又反过来调用它。

int function1(int value1) {
   if(value1 < 1)
      return;
   function2(value1 - 1);
   printf("%d ",value1);   
}
int function2(int value2) {
   function1(value2);
}

属性

递归函数可能像循环一样无限运行。为了避免递归函数无限运行，递归函数必须具有两个属性：

• 基本条件 - 必须至少有一个基本条件，当满足此条件时，函数停止递归调用自身。

• 渐进式方法 - 递归调用应该以这样的方式进行，每次进行递归调用时都更接近基本条件。

实现

许多编程语言通过栈来实现递归。通常，每当一个函数（调用者）调用另一个函数（被调用者）或自身作为被调用者时，调用者函数将执行控制转移给被调用者。此转移过程可能还涉及一些数据从调用者传递给被调用者。

这意味着调用者函数必须暂时暂停其执行，并在执行控制从被调用者函数返回时恢复。在这里，调用者函数需要从其暂停执行的点开始精确地执行。它还需要它正在处理的完全相同的数据值。为此，将为调用者函数创建一个激活记录（或堆栈帧）。

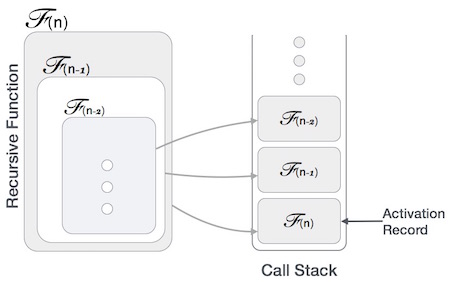
此激活记录保存有关局部变量、形式参数、返回地址以及传递给调用者函数的所有信息。

递归分析

有人可能会质疑为什么要使用递归，因为可以使用迭代来完成相同的任务。第一个原因是，递归使程序更易于阅读，并且由于最新的增强型CPU系统，递归比迭代更有效。

时间复杂度

对于迭代，我们采用迭代次数来计算时间复杂度。同样，对于递归，假设一切都是常数，我们试图找出递归调用的次数。对函数的调用为O(1)，因此递归调用n次使得递归函数为O(n)。

空间复杂度

空间复杂度计算的是模块执行需要多少额外空间。对于迭代，编译器几乎不需要任何额外空间。编译器不断更新迭代中使用的变量的值。但是对于递归，系统需要在每次进行递归调用时存储激活记录。因此，认为递归函数的空间复杂度可能高于具有迭代的函数。

示例

以下是各种编程语言中递归的实现：

// C program for Recursion Data Structure
#include <stdio.h>
int factorial(int n) {
    // Base case: factorial of 0 is 1
    if (n == 0)
        return 1;
    // Recursive case: multiply n with factorial of (n-1)
    return n * factorial(n - 1);
}
int main() {
    // case 1
    int number = 6;
    printf("Number is: %d\n" , 6);
    //case 2
    if (number < 0) {
        printf("Error: Factorial is undefined for negative numbers.\n");
        return 1;
    } 
    int result = factorial(number);
    //print the output
    printf("Factorial of %d is: %d\n", number, result);
    return 0;
}

Number is: 6
Factorial of 6 is: 720

// CPP program for Recursion Data Structure
#include <iostream>
int factorial(int n) {
    // Base case: factorial of 0 is 1
    if (n == 0)
        return 1;  
    // Recursive case: multiply n with factorial of (n-1)
    return n * factorial(n - 1);
}
int main() {
    // case 1
    int number = 6;
    std::cout<<"Number is: "<<number<<"\n";
    //case 2
    if (number < 0) {
        std::cout << "Error: Factorial is undefined for negative numbers.\n";
        return 1;
    }
    int result = factorial(number);
    //print the output
    std::cout << "Factorial of " << number << " is: " << result << std::endl;  
    return 0;
}

Number is:  6
Factorial of 6 is: 720

// Java program for Recursion Data Structure
import java.util.Scanner;
public class Main {
    public static int factorial(int n) {
        // Base case: factorial of 0 is 1
        if (n == 0)
            return 1;
        // Recursive case: multiply n with factorial of (n-1)
        return n * factorial(n - 1);
    }
    public static void main(String[] args) {
        //Case 1
        int number = 6;
		System.out.println("Number is: " + number);
        //Case 2
        if (number < 0) {
            System.out.println("Error: Factorial is undefined for negative numbers.");
            System.exit(1);
        }
        int result = factorial(number);
        //print the output
        System.out.println("Factorial of " + number + " is: " + result);
    }
}

Number is: 6
Factorial of 6 is: 720

# Python program for Recursion Data Structure
def factorial(n):
    #Base Case: factorial of 0 is 1
    if n == 0:
        return 1
    # Recursive case: multiply n with factorial of (n-1)
    return n * factorial(n - 1)
#Case 1:
number = 6;
print("Number is: ", number);
#Case 2:
if number < 0:
    print("Error: Factorial is undefined for negative numbers.")
else:
    result = factorial(number)
    # print the output
    print("Factorial of", number, "is: ", result)

Number is:  6
Factorial of 6 is: 720