堆数据结构

Table of content
上一页
下一页

堆是平衡二叉树数据结构的一种特殊情况，其中根节点键与其子节点进行比较并相应地排列。如果α有子节点β，则-

key(α) ≥ key(β)

由于父节点的值大于子节点的值，因此此属性生成最大堆。根据此标准，堆可以分为两种类型-

For Input → 35 33 42 10 14 19 27 44 26 31

最小堆 - 其中根节点的值小于或等于其任何一个子节点。

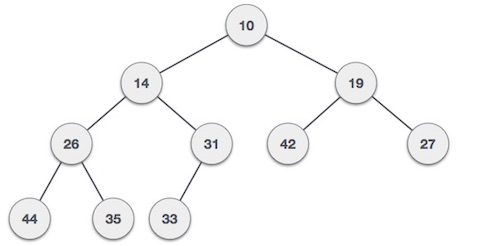
Max Heap Example

最大堆 - 其中根节点的值大于或等于其任何一个子节点。

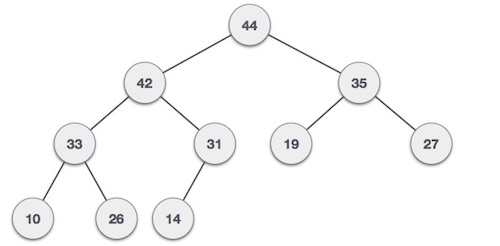
Max Heap Example

两棵树都是使用相同的输入和到达顺序构建的。

最大堆构建算法

我们将使用相同的示例来演示如何创建最大堆。创建最小堆的过程类似，但我们选择最小值而不是最大值。

我们将通过一次插入一个元素来推导出最大堆的算法。在任何时间点，堆都必须保持其属性。在插入过程中，我们还假设我们将节点插入到一个已经堆化的树中。

Step 1 − Create a new node at the end of heap.
Step 2 − Assign new value to the node.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.

注意 - 在最小堆构建算法中，我们期望父节点的值小于子节点的值。

让我们通过动画插图来了解最大堆的构建。我们考虑之前使用的相同输入示例。

Max Heap Animated Example

示例

以下是此操作在各种编程语言中的实现-

C C++ Java Python
//C code for Max Heap construction  Algorithm
#include <stdio.h>
#include <stdlib.h>
// Structure to represent a heap
typedef struct {
    int* array;     // Array to store heap elements
    int capacity;   // Maximum capacity of the heap
    int size;       // Current size of the heap
} Heap;
// Function to create a new heap
Heap* createHeap(int capacity)
{
    Heap* heap = (Heap*)malloc(sizeof(Heap));
    heap->array = (int*)malloc(capacity * sizeof(int));
    heap->capacity = capacity;
    heap->size = 0;
    return heap;
}
// Function to swap two elements in the heap
void swap(int* a, int* b)
{
    int temp = *a;
    *a = *b;
    *b = temp;
}
// Function to heapify a subtree rooted at index i
void heapify(Heap* heap, int i)
{
    int largest = i;
    int left = 2 * i + 1;
    int right = 2 * i + 2;
    // Check if the left child is larger than the root
    if (left < heap->size && heap->array[left] > heap->array[largest])
        largest = left;
    // Check if the right child is larger than the largest so far
    if (right < heap->size && heap->array[right] > heap->array[largest])
        largest = right;
    // If the largest is not the root, swap the root with the largest
    if (largest != i) {
        swap(&heap->array[i], &heap->array[largest]);
        heapify(heap, largest);
    }
}
// Function to insert a new element into the heap
void insert(Heap* heap, int value)
{
    if (heap->size == heap->capacity) {
        printf("Heap is full. Cannot insert more elements.\n");
        return;
    }
    // Insert the new element at the end
    int i = heap->size++;
    heap->array[i] = value;
    // Fix the heap property if it is violated
    while (i != 0 && heap->array[(i - 1) / 2] < heap->array[i]) {
        swap(&heap->array[i], &heap->array[(i - 1) / 2]);
        i = (i - 1) / 2;
    }
}
// Function to extract the maximum element from the heap
int extractMax(Heap* heap)
{
    if (heap->size == 0) {
        printf("Heap is empty. Cannot extract maximum element.\n");
        return -1;
    }
    // Store the root element
    int max = heap->array[0];
    // Replace the root with the last element
    heap->array[0] = heap->array[heap->size - 1];
    heap->size--;
    // Heapify the root
    heapify(heap, 0);
    return max;
}
// Function to print the elements of the heap
void printHeap(Heap* heap)
{
    printf("Heap elements: ");
    for (int i = 0; i < heap->size; i++) {
        printf("%d ", heap->array[i]);
    }
    printf("\n");
}
// Example usage of the heap
int main()
{
    Heap* heap = createHeap(10);
    insert(heap, 35);
    insert(heap, 33);
    insert(heap, 42);
    insert(heap, 10);
    insert(heap, 14);
    insert(heap, 19);
    insert(heap, 27);
    insert(heap, 44);
    insert(heap, 26);
    insert(heap, 31);
    printHeap(heap);
    int max = extractMax(heap);
    printf("Maximum element: %d\n", max);
    return 0;
}

输出

Heap elements: 44 42 35 33 31 19 27 10 26 14 
Maximum element: 44

//C++ code for Max Heap construction  Algorithm
#include <iostream>
// Structure to represent a heap
struct Heap {
    int* array;     // Array to store heap elements
    int capacity;   // Maximum capacity of the heap
    int size;       // Current size of the heap
};
// Function to create a new heap
Heap* createHeap(int capacity)
{
    Heap* heap = new Heap;
    heap->array = new int[capacity];
    heap->capacity = capacity;
    heap->size = 0;
    return heap;
}
// Function to swap two elements in the heap
void swap(int& a, int& b)
{
    int temp = a;
    a = b;
    b = temp;
}
// Function to heapify a subtree rooted at index i
void heapify(Heap* heap, int i)
{
    int largest = i;
    int left = 2 * i + 1;
    int right = 2 * i + 2;
    // Check if the left child is larger than the root
    if (left <heap->size && heap->array[left] > heap->array[largest])
        largest = left;
    // Check if the right child is larger than the largest so far
    if (right <heap->size && heap->array[right] > heap->array[largest])
        largest = right;
    // If the largest is not the root, swap the root with the largest
    if (largest != i) {
        swap(heap->array[i], heap->array[largest]);
        heapify(heap, largest);
    }
}
// Function to insert a new element into the heap
void insert(Heap* heap, int value)
{
    if (heap->size == heap->capacity) {
        std::cout << "Heap is full. Cannot insert more elements." << std::endl;
        return;
    }
    // Insert the new element at the end
    int i = heap->size++;
    heap->array[i] = value;
    // Fix the heap property if it is violated
    while (i != 0 && heap->array[(i - 1) / 2] < heap->array[i]) {
        swap(heap->array[i], heap->array[(i - 1) / 2]);
        i = (i - 1) / 2;
    }
}
// Function to extract the maximum element from the heap
int extractMax(Heap* heap)
{
    if (heap->size == 0) {
        std::cout << "Heap is empty. Cannot extract maximum element." << std::endl;
        return -1;
    }
    // Store the root element
    int max = heap->array[0];
    // Replace the root with the last element
    heap->array[0] = heap->array[heap->size - 1];
    heap->size--;
    // Heapify the root
    heapify(heap, 0);
    return max;
}
// Function to print the elements of the heap
void printHeap(Heap* heap)
{
    std::cout << "Heap elements: ";
    for (int i = 0; i < heap->size; i++) {
        std::cout << heap->array[i] << " ";
    }
    std::cout << std::endl;
}
// Example usage of the heap
int main()
{
    Heap* heap = createHeap(10);
    insert(heap, 35);
    insert(heap, 33);
    insert(heap, 42);
    insert(heap, 10);
    insert(heap, 14);
    insert(heap, 19);
    insert(heap, 27);
    insert(heap, 44);
    insert(heap, 26);
    insert(heap, 31);

    printHeap(heap);

    int max = extractMax(heap);
    std::cout << "Maximum element: " << max << std::endl;

    return 0;
}

输出

Heap elements: 44 42 35 33 31 19 27 10 26 14 
Maximum element: 44

// Java code for for Max Heap construction  Algorithm
//Structure to represent a heap
public class MaxHeap {
    private int[] heap; // To store heap elements
    private int capacity; // Maximum capacity of the heap
    private int size; // Current size of the heap
    // To create a new heap
    public MaxHeap(int capacity) {
        this.capacity = capacity;
        this.size = 0;
        this.heap = new int[capacity];
    }
    private int parent(int i) {
        return (i - 1) / 2;
    }
    private int leftChild(int i) {
        return 2 * i + 1;
    }
    private int rightChild(int i) {
        return 2 * i + 2;
    }
    private void swap(int i, int j) {
        int temp = heap[i];
        heap[i] = heap[j];
        heap[j] = temp;
    }
   // Heapify a subtree rooted at index i
    private void heapifyDown(int i) {
        int largest = i;
        int left = leftChild(i);
        int right = rightChild(i);     
        // Check if the left child is larger than the root
        if (left < size && heap[left] > heap[largest])
            largest = left;         
        // Check if the right child is larger than the largest so far
        if (right < size && heap[right] > heap[largest])
            largest = right;
        // If the largest is not the root, swap the root with the largest
        if (largest != i) {
            swap(i, largest);
            heapifyDown(largest);
        }
    }
    private void heapifyUp(int i) {
        while (i > 0 && heap[i] > heap[parent(i)]) {
            int parent = parent(i);
            swap(i, parent);
            i = parent;
        }
    }
    // Insert the new element at the end
    public void insert(int value) {
        if (size == capacity) {
            System.out.println("Heap is full. Cannot insert more elements.");
            return;
        }
        heap[size] = value;
        size++;
        heapifyUp(size - 1);
    }
    // Function to extract the maximum element from the heap
    public int extractMax() {
        if (size == 0) {
            System.out.println("Heap is empty. Cannot extract maximum element.");
            return -1;
        }
        // store th root element
        int max = heap[0];
        //Replace the root with the last elements
        heap[0] = heap[size - 1];
        size--;
        heapifyDown(0);
        return max;
    } 
    //print the elements of the heap
    public void printHeap() {
        System.out.print("Heap elements: ");
        for (int i = 0; i < size; i++) {
            System.out.print(heap[i] + " ");
        }
        System.out.println();
    }
    public static void main(String[] args) {
        MaxHeap heap = new MaxHeap(10);
        heap.insert(35);
        heap.insert(33);
        heap.insert(42);
        heap.insert(10);
        heap.insert(14);
        heap.insert(19);
        heap.insert(27);
        heap.insert(44);
        heap.insert(26);
        heap.insert(31);
        heap.printHeap();
        int max = heap.extractMax();
        System.out.println("Maximum element: " + max);
    }
}

输出

Heap elements: 44 42 35 33 31 19 27 10 26 14 
Maximum element: 44

# Python code for for Max Heap construction  Algorithm
class MaxHeap:
    def __init__(self):
        self.heap = []
    def parent(self, i):
        return (i - 1) // 2
    def left_child(self, i):
        return 2 * i + 1
    def right_child(self, i):
        return 2 * i + 2
    #Function to swap two elements in the heap
    def swap(self, i, j):
        self.heap[i], self.heap[j] = self.heap[j], self.heap[i]
    # Function to heapify a subtree rooted at index i
    def heapify_down(self, i):
        left = self.left_child(i)
        right = self.right_child(i)
        largest = i
        #Check if the left child is larger than the root
        if left < len(self.heap) and self.heap[left] >self.heap[largest]:
            largest = left
        # Check if the right child is larger than the largest so far
        if right < len(self.heap) and self.heap[right] > self.heap[largest]:
            largest = right

        # If the largest is not the root, swap the root with the largest
        if largest != i:
            self.swap(i, largest)
            self.heapify_down(largest)
    def heapify_up(self, i):
        while i > 0 and self.heap[i] > self.heap[self.parent(i)]:
            parent = self.parent(i)
            self.swap(i, parent)
            i = parent
    # Insert the new element at the end
    def insert(self, value):
        self.heap.append(value)
        # Fix the heap property if it is violated
        self.heapify_up(len(self.heap) - 1)
    # Function to extract the maximum element from the heap
    def extract_max(self):
        if len(self.heap) == 0:
            print("Heap is empty. Cannot extract maximum element.")
            return None
        max_value = self.heap[0]
        self.heap[0] = self.heap[-1]
        self.heap.pop()
        self.heapify_down(0)
        return max_value
    # Function to print the elements of the heap
    def print_heap(self):
        print("Heap elements:", end=" ")
        for value in self.heap:
            print(value, end=" ")
        print()
# Example usage of the heap
heap = MaxHeap()
heap.insert(35)
heap.insert(33)
heap.insert(42)
heap.insert(10)
heap.insert(14)
heap.insert(19)
heap.insert(27)
heap.insert(44)
heap.insert(26)
heap.insert(31)
heap.print_heap()
max_value = heap.extract_max()
print("Maximum element:", max_value)

输出

Heap elements: 44 42 35 33 31 19 27 10 26 14 
Maximum element: 44s

最大堆删除算法

让我们推导出一个从最大堆中删除的算法。在最大（或最小）堆中，删除总是发生在根节点以删除最大（或最小）值。

Step 1 − Remove root node.
Step 2 − Move the last element of last level to root.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.
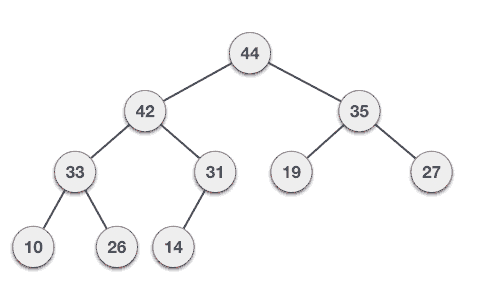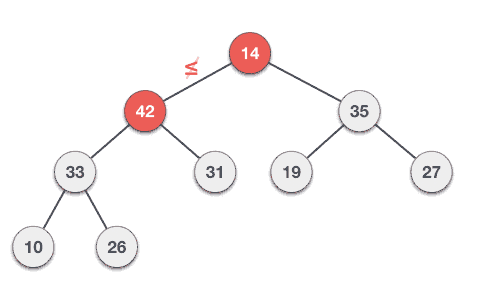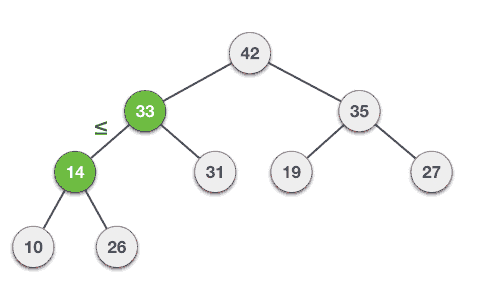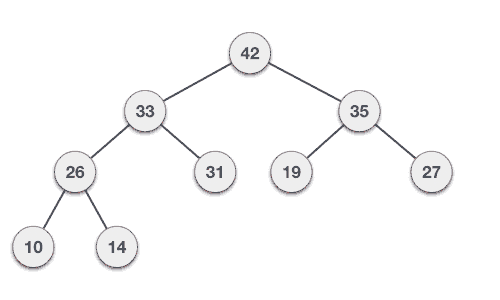
Max Heap Deletion Animated Example

示例

以下是此操作在各种编程语言中的实现-

C C++ Java Python
//C code for Max Heap Deletion Algorithm
#include <stdio.h>
#include <stdlib.h>
// Structure to represent a heap
typedef struct {
    int* array;     // Array to store heap elements
    int capacity;   // Maximum capacity of the heap
    int size;       // Current size of the heap
} Heap;
// create a new heap
Heap* createHeap(int capacity)
{
    Heap* heap = (Heap*)malloc(sizeof(Heap));
    heap->array = (int*)malloc(capacity * sizeof(int));
    heap->capacity = capacity;
    heap->size = 0;
    return heap;
}
// swap two elements in the heap
void swap(int* a, int* b)
{
    int temp = *a;
    *a = *b;
    *b = temp;
}
// Heapify a subtree rooted at index i
void heapify(Heap* heap, int i)
{
    int largest = i;
    int left = 2 * i + 1;
    int right = 2 * i + 2;
    // Check if the left child is larger than the root
    if (left < heap->size && heap->array[left] > heap->array[largest])
        largest = left;
    // Check if the right child is larger than the largest so far
    if (right < heap->size && heap->array[right] > heap->array[largest])
        largest = right;
    // If the largest is not the root, swap the root with the largest
    if (largest != i) {
        swap(&heap->array[i], &heap->array[largest]);
        heapify(heap, largest);
    }
}
// Function to insert a new element into the heap
void insert(Heap* heap, int value)
{
    if (heap->size == heap->capacity) {
        printf("Heap is full. Cannot insert more elements.\n");
        return;
    }
    // Insert the new element at the end
    int i = heap->size++;
    heap->array[i] = value;
    // Fix the heap property if it is violated
    while (i != 0 && heap->array[(i - 1) / 2] < heap->array[i]) {
        swap(&heap->array[i], &heap->array[(i - 1) / 2]);
        i = (i - 1) / 2;
    }
}
// delete the maximum element from the heap
int deleteMax(Heap* heap)
{
    if (heap->size == 0) {
        printf("Heap is empty. Cannot extract maximum element.\n");
        return -1;
    }
    // Store the root element
    int max = heap->array[0];
    // Replace the root with the last element
    heap->array[0] = heap->array[heap->size - 1];
    heap->size--;
    // Heapify the root
    heapify(heap, 0);
    return max;
}
// print the elements of the heap
void printHeap(Heap* heap)
{
    for (int i = 0; i < heap->size; i++) {
        printf("%d ", heap->array[i]);
    }
    printf("\n");
}
// Deallocate memory occupied by the heap
void destroyHeap(Heap* heap)
{
    free(heap->array);
    free(heap);
}
// Example usage of the heap
int main()
{
    Heap* heap = createHeap(10);
    insert(heap, 35);
    insert(heap, 33);
    insert(heap, 42);
    insert(heap, 10);
    insert(heap, 14);
    insert(heap, 19);
    insert(heap, 27);
    insert(heap, 44);
    insert(heap, 26);
    insert(heap, 31);
	printf("Heap elements before deletion: ");
    printHeap(heap);
    // Deleting the maximum element in the heap
    int max = deleteMax(heap);
    printf("Maximum element: %d\n", max);
	printf("Heap elements after deletion: ");
    printHeap(heap);
    destroyHeap(heap);
    return 0;
}

输出

Heap elements before deletion: 44 42 35 33 31 19 27 10 26 14 
Maximum element: 44
Heap elements after deletion: 42 33 35 26 31 19 27 10 14

//C++ code for Max Heap Deletion Algorithm
#include <iostream>
// Structure to represent a heap
struct Heap {
    int* array;     // Array to store heap elements
    int capacity;   // Maximum capacity of the heap
    int size;       // Current size of the heap
};
// Create a new heap
Heap* createHeap(int capacity)
{
    Heap* heap = new Heap;
    heap->array = new int[capacity];
    heap->capacity = capacity;
    heap->size = 0;
    return heap;
}
// Swap two elements in the heap
void swap(int& a, int& b)
{
    int temp = a;
    a = b;
    b = temp;
}
// Heapify a subtree rooted at index i
void heapify(Heap* heap, int i)
{
    int largest = i;
    int left = 2 * i + 1;
    int right = 2 * i + 2;
    // Check if the left child is larger than the root
    if (left < heap->size && heap->array[left] > heap->array[largest])
        largest = left;
    // Check if the right child is larger than the largest so far
    if (right < heap->size && heap->array[right] > heap->array[largest])
        largest = right;
    // If the largest is not the root, swap the root with the largest
    if (largest != i) {
        swap(heap->array[i], heap->array[largest]);
        heapify(heap, largest);
    }
}
// Function to insert a new element into the heap
void insert(Heap* heap, int value)
{
    if (heap->size == heap->capacity) {
        std::cout << "Heap is full. Cannot insert more elements." << std::endl;
        return;
    }
    // Insert the new element at the end
    int i = heap->size++;
    heap->array[i] = value;

    // Fix the heap property if it is violated
    while (i != 0 && heap->array[(i - 1) / 2] < heap->array[i]) {
        swap(heap->array[i], heap->array[(i - 1) / 2]);
        i = (i - 1) / 2;
    }
}
// Function to delete the maximum element from the heap
int deleteMax(Heap* heap)
{
    if (heap->size == 0) {
        std::cout << "Heap is empty. Cannot extract maximum element." << std::endl;
        return -1;
    }
    // Store the root element
    int max = heap->array[0];
    // Replace the root with the last element
    heap->array[0] = heap->array[heap->size - 1];
    heap->size--;
    // Heapify the root
    heapify(heap, 0);

    return max;
}
// Function to print the elements of the heap
void printHeap(Heap* heap)
{
    for (int i = 0; i < heap->size; i++) {
        std::cout << heap->array[i] << " ";
    }
    std::cout << std::endl;
}
// Function to deallocate memory occupied by the heap
void destroyHeap(Heap* heap)
{
    delete[] heap->array;
    delete heap;
}
// Example usage of the heap
int main()
{
    Heap* heap = createHeap(10);
    insert(heap, 35);
    insert(heap, 33);
    insert(heap, 42);
    insert(heap, 10);
    insert(heap, 14);
    insert(heap, 19);
    insert(heap, 27);
    insert(heap, 44);
    insert(heap, 26);
    insert(heap, 31);
	std::cout << "Heap elements before deletion: ";
    printHeap(heap);
    int max = deleteMax(heap);
    std::cout << "Maximum element: " << max << std::endl;
	std::cout << "Heap elements after deletion: ";
    printHeap(heap);
    destroyHeap(heap);
    return 0;
}

输出

Heap elements before deletion: 44 42 35 33 31 19 27 10 26 14 
Maximum element: 44
Heap elements after deletion: 42 33 35 26 31 19 27 10 14 

// Java code for for Max Heap Deletion  Algorithm
// Structure to represent a heap
class Heap {
    private int[] array;  // Array to store heap elements
    private int capacity;  // Maximum capacity of the heap
    private int size;      // Current size of the heap
    // To create a new heap
    public Heap(int capacity) {
        this.array = new int[capacity];
        this.capacity = capacity;
        this.size = 0;
    }
    // Swap two elements in the heap
    private void swap(int a, int b) {
        int temp = array[a];
        array[a] = array[b];
        array[b] = temp;
    }
    // Heapify a subtree rooted at index i
    private void heapify(int i) {
        int largest = i;
        int left = 2 * i + 1;
        int right = 2 * i + 2;     
        // Check if the left child is larger than the root
        if (left < size && array[left] > array[largest])
            largest = left;         
        // Check if the right child is larger than the largest so far
        if (right < size && array[right] > array[largest])
            largest = right;
        // If the largest is not the root, swap the root with the largest
        if (largest != i) {
            swap(i, largest);
            heapify(largest);
        }
    }
    // Insert a new element into the heap
    public void insert(int value) {
        if (size == capacity) {
            System.out.println("Heap is full. Cannot insert more elements.");
            return;
        }
        // Insert the new element at the end
        int i = size++;
        array[i] = value;
        // Fix the heap property if it is violated
        while (i != 0 && array[(i - 1) / 2] < array[i]) {
            swap(i, (i - 1) / 2);
            i = (i - 1) / 2;
        }
    }
    // Delete the maximum element from the heap
    public int deleteMax() {
        if (size == 0) {
            System.out.println("Heap is empty. Cannot extract maximum element.");
            return -1;
        }
        // Store the root element
        int max = array[0];
        // Replace the root with the last element
        array[0] = array[size - 1];
        size--;
        // Heapify the root
        heapify(0);
        return max;
    }
    // Print the elements of the heap
    public void printHeap() {
        for (int i = 0; i < size; i++) {
            System.out.print(array[i] + " ");
        }
        System.out.println();
    }
    // Deallocate memory occupied by the heap
    public void destroyHeap() {
        array = null;
        size = 0;
    }
}
//Inserting the elements
public class Main {
    public static void main(String[] args) {
        Heap heap = new Heap(10);
        heap.insert(35);
        heap.insert(33);
        heap.insert(42);
        heap.insert(10);
        heap.insert(14);
        heap.insert(19);
        heap.insert(27);
        heap.insert(44);
        heap.insert(26);
        heap.insert(31);
		System.out.print("Heap elements before deletion: ");
        heap.printHeap();
        int max = heap.deleteMax();
        System.out.println("Maximum element: " + max);  
        //Printing the heap elements after deletion of max element
		System.out.print("Heap elements after deletion: ");
        heap.printHeap();
        heap.destroyHeap();
    }
}

输出

Heap elements before deletion: 44 42 35 33 31 19 27 10 26 14 
Maximum element: 44
Heap elements after deletion: 42 33 35 26 31 19 27 10 14 

#Python code for Max Heap Deletion Algorithm
class Heap:
    def __init__(self, capacity):
        self.array = [0] * capacity  #array to store heap elements
        self.capacity = capacity  #maximum capacity of the heap
        self.size = 0  #Current size of the heap
    # swap two elements in the heap
    def swap(self, a, b):
        self.array[a], self.array[b] = self.array[b], self.array[a]
    # Heapify a subtree rooted at index i
    def heapify(self, i):
        largest = i
        left = 2 * i + 1
        right = 2 * i + 2
        # Check if the left child is larger than the root
        if left < self.size and self.array[left] > self.array[largest]:
            largest = left
        # Check if the right child is larger than the largest so far
        if right < self.size and self.array[right] > self.array[largest]:
            largest = right
        # If the largest is not the root, swap the root with the largest
        if largest != i:
            self.swap(i, largest)
            self.heapify(largest)
    # insert a new element into the heap
    def insert(self, value):
        if self.size == self.capacity:
            print("Heap is full. Cannot insert more elements.")
            return
        # Insert the new element at the end
        i = self.size
        self.size += 1
        self.array[i] = value
        # Fix the heap property if it is violated
        while i != 0 and self.array[(i - 1) // 2] < self.array[i]:
            self.swap(i, (i - 1) // 2)
            i = (i - 1) // 2
    # delete the maximum element from the heap
    def deleteMax(self):
        if self.size == 0:
            print("Heap is empty. Cannot extract maximum element.")
            return -1
        # store the root element
        max_value = self.array[0]
        # Replace the root with the last element
        self.array[0] = self.array[self.size - 1]
        self.size -= 1
        # Heapify the root
        self.heapify(0)
        return max_value
    # print the elements of the heap
    def printHeap(self):
        for i in range(self.size):
            print(self.array[i], end=" ")
        print()
    # deallocate memory occupied by the heap
    def destroyHeap(self):
        self.array = []
        self.size = 0
# Example usage of the heap
heap = Heap(10)
heap.insert(35)
heap.insert(33)
heap.insert(42)
heap.insert(10)
heap.insert(14)
heap.insert(19)
heap.insert(27)
heap.insert(44)
heap.insert(26)
heap.insert(31)
print("Heap elements before deletion:", end=" ")
heap.printHeap()
max_value = heap.deleteMax()
print("Maximum element:", max_value)
print("Heap elements after deletion:", end=" ")
heap.printHeap()
heap.destroyHeap()

输出

Heap elements before deletion: 44 42 35 33 31 19 27 10 26 14 
Maximum element: 44
Heap elements after deletion: 42 33 35 26 31 19 27 10 14
打印页面
上一页
下一页
广告