树形数据结构

---

---

树形数据结构

树是一种非线性的抽象数据类型，具有层次结构。它由节点（存储数据的地方）通过链接连接而成。树形数据结构源于单个称为根节点的节点，并具有连接到根的子树。

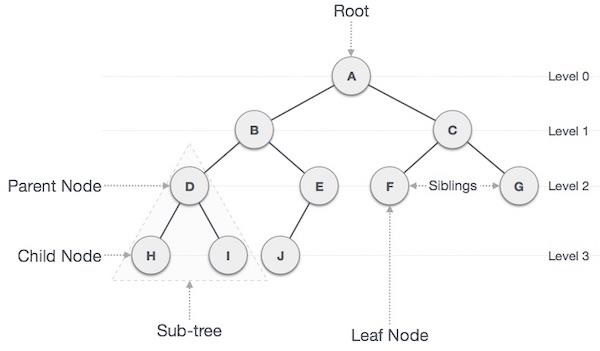
重要术语

以下是关于树的重要术语。

• 路径 − 路径指的是沿着树的边的节点序列。

• 根 − 树顶部的节点称为根。每棵树只有一个根，并且从根节点到任何节点只有一条路径。

• 父节点 − 除根节点外的任何节点都有一条向上连接到称为父节点的节点的边。

• 子节点 − 下方由其向下边连接的给定节点称为其子节点。

• 叶子节点 − 没有子节点的节点称为叶子节点。

• 子树 − 子树表示节点的后代。

• 访问 − 访问是指当控制处于节点上时检查节点的值。

• 遍历 − 遍历意味着以特定顺序通过节点。

• 层级 − 节点的层级表示节点的代数。如果根节点在第0层，则其下一个子节点在第1层，其孙子节点在第2层，依此类推。

• 键 − 键表示节点的值，根据该值将对节点进行搜索操作。

树的类型

树有三种类型：

• 一般树

• 二叉树

• 二叉搜索树

一般树

一般树是非有序的树形数据结构，其中根节点最多有0个或n个子树。

一般树对它们的层次结构没有约束。因此，根节点充当所有其他子树的超集。

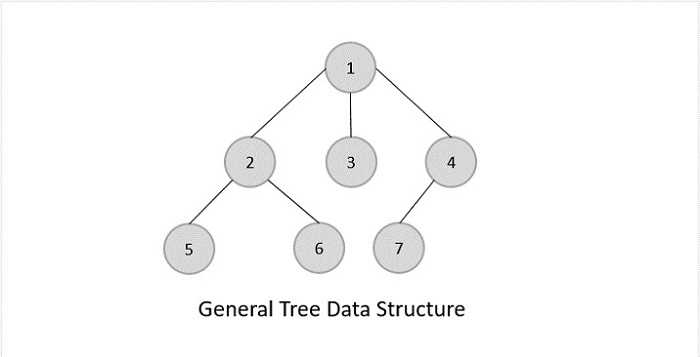
二叉树

二叉树是一般树，其中根节点最多只能包含2个子树：左子树和右子树。根据子节点的数量，二叉树分为三种类型。

满二叉树

• 满二叉树是一种二叉树类型，其中每个节点都具有0个或2个子节点。

完全二叉树

• 完全二叉树是一种二叉树类型，其中所有叶子节点都必须位于同一层。但是，完全二叉树中的根节点和内部节点可以具有0、1或2个子节点。

完美二叉树

• 完美二叉树是一种二叉树类型，其中所有叶子节点都位于同一层，并且除叶子节点外的每个节点都有2个子节点。

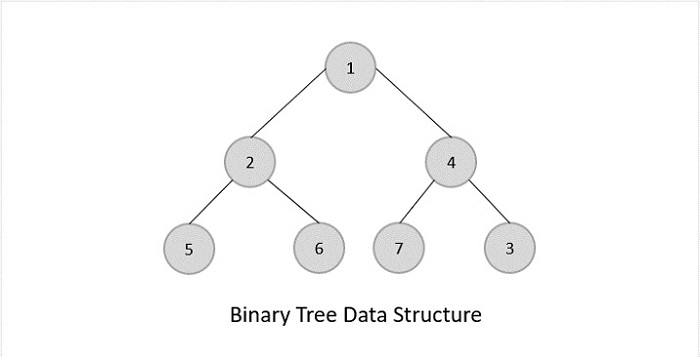
二叉搜索树

二叉搜索树具有二叉树的所有属性，包括一些基于某些约束的额外属性，使其比二叉树更有效。

二叉搜索树 (BST) 中的数据总是以这样的方式存储：左子树中的值总是小于根节点中的值，而右子树中的值总是大于根节点中的值，即左子树 < 根节点 ≤ 右子树。

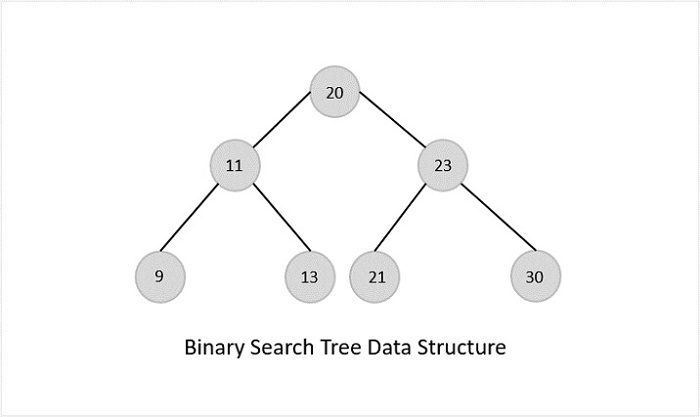
BST 的优点

• 二叉搜索树比二叉树更有效，因为执行各种操作的时间复杂度降低了。

• 由于键的顺序仅基于父节点，因此搜索操作变得更简单。

• BST 的排列也有利于范围查询，范围查询用于查找两个键之间存在的值。这有助于数据库管理系统。

BST 的缺点

二叉搜索树的主要缺点是，如果节点中的所有元素都大于或小于根节点，树将变得倾斜。简单地说，树完全倾斜到一边。

这种倾斜将使树成为链表而不是 BST，因为搜索操作的最坏情况时间复杂度变为 O(n)。

为了克服二叉搜索树的倾斜问题，引入了平衡二叉搜索树的概念。

平衡二叉搜索树

考虑一个二叉搜索树，其中左子树的高度为“m”，右子树的高度为“n”。如果 (m-n) 的值为 0、1 或 -1，则该树被称为平衡二叉搜索树。

树的设计方式是在高度差超过 1 时自动平衡。二叉搜索树使用旋转作为自平衡算法。有四种不同的旋转类型：左左、右右、左右、右左。

有各种类型的自平衡二叉搜索树：

• AVL 树

• 红黑树

• B 树

• B+ 树

• 伸展树

• 优先搜索树