图数据结构

上一页
下一页

什么是图？

图是一种抽象数据类型 (ADT)，它由一组通过链接相互连接的对象组成。相互连接的对象由称为顶点的点表示，连接顶点的链接称为边。

正式地说，图是一对集合(V, E)，其中V是顶点的集合，E是连接顶点对的边的集合。请看下面的图：

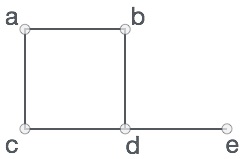
Graph Basics

在上图中，

V = {a, b, c, d, e}

E = {ab, ac, bd, cd, de}

图数据结构

数学图可以用数据结构表示。我们可以使用顶点数组和二维边数组来表示图。在我们继续之前，让我们熟悉一些重要的术语：

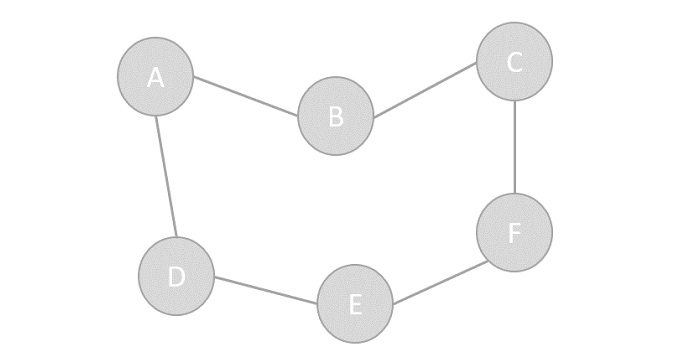
  • 顶点 - 图的每个节点都表示为一个顶点。在下面的例子中，带标签的圆圈代表顶点。因此，A到G都是顶点。我们可以用数组来表示它们，如下图所示。这里A可以用索引0标识，B可以用索引1标识，以此类推。

  • 边 - 边表示两个顶点之间的路径或两点之间的线。在下面的例子中，从A到B、B到C等的线表示边。我们可以使用二维数组来表示数组，如下图所示。这里AB可以用第0行第1列的1表示，BC可以用第1行第2列的1表示，以此类推，其他组合保持为0。

  • 邻接 - 如果两个节点或顶点通过一条边相互连接，则它们是邻接的。在下面的例子中，B与A邻接，C与B邻接，以此类推。

  • 路径 - 路径表示两个顶点之间的一系列边。在下面的例子中，ABCD表示从A到D的路径。

graph graph

图的操作

图的主要操作包括创建一个带有顶点和边的图，以及显示该图。但是，使用图执行的最常见和最流行的操作之一是遍历，即以特定顺序访问图的每个顶点。

图中有两种类型的遍历：

深度优先搜索遍历

深度优先搜索是一种遍历算法，它按照其深度的递减顺序访问图的所有顶点。在这个算法中，选择一个任意节点作为起点，通过标记未访问的邻接节点来回遍历图，直到所有顶点都被标记。

DFS遍历使用栈数据结构来跟踪未访问的节点。

点击查看 深度优先搜索遍历

广度优先搜索遍历

广度优先搜索是一种遍历算法，它在移动到下一层深度之前访问图中同一层深度上存在的所有顶点。在这个算法中，选择一个任意节点作为起点，通过访问同一深度级别上的邻接顶点并标记它们来遍历图，直到没有剩余顶点。

DFS遍历使用队列数据结构来跟踪未访问的节点。

点击查看 广度优先搜索遍历

图的表示

在表示图时，我们必须仔细描绘图中存在的元素（顶点和边）以及它们之间的关系。图解地，图用有限的节点集和它们之间的连接链接来表示。但是，我们也可以用其他最常用的方式表示图，例如：

  • 邻接矩阵

  • 邻接表

邻接矩阵

邻接矩阵是一个 V x V 矩阵，其值填充为 0 或 1。如果 Vi 和 Vj 之间存在链接，则记录为 1；否则为 0。

对于下面给定的图，让我们构造一个邻接矩阵：

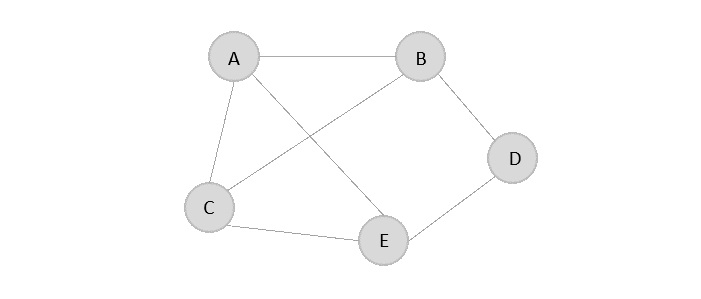
Adjacency_Matrix

邻接矩阵是：

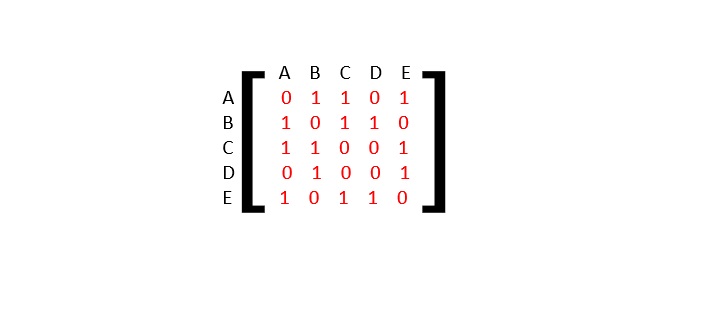
adjacency_matrix

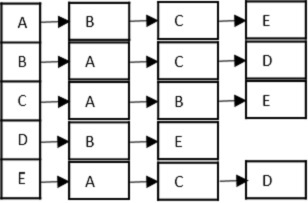
邻接表

邻接表是直接连接到图中其他顶点的顶点的列表。

Adjacency_Matrix

邻接表是：

adjacency list

图的类型

图主要有两种类型：

  • 有向图

  • 无向图

顾名思义，有向图由具有方向的边组成，这些方向要么远离顶点，要么指向顶点。无向图的边完全没有方向。

Directed Graph

有向图

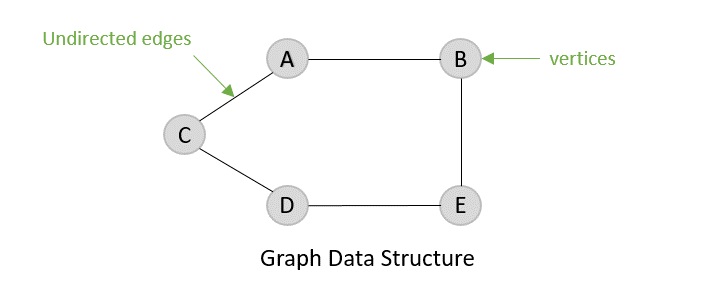
Undirected_Grap

无向图

生成树

一个生成树是无向图的子集，它包含以图中最小数量的边连接在一起的图的所有顶点。精确地说，生成树的边是原始图中边的子集。

如果图中的所有顶点都连接在一起，则至少存在一个生成树。在一个图中，可能存在多个生成树。

属性

  • 生成树没有任何环。

  • 可以从任何其他顶点到达任何顶点。

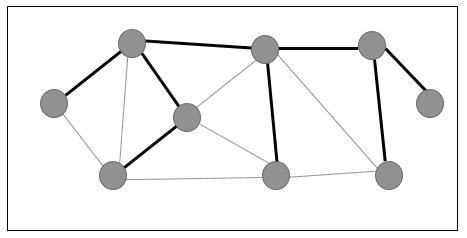
示例

在下图中，突出显示的边构成一个生成树。

Spanning Tree

最小生成树

最小生成树 (MST) 是连接加权无向图的所有顶点的边的一个子集，其总边权重最小。要导出 MST，可以使用 Prim 算法或 Kruskal 算法。因此，我们将在本章中讨论 Prim 算法。

正如我们所讨论的，一个图可能有多个生成树。如果有 n 个顶点，则生成树应具有 n − 1 个边。在这种情况下，如果图的每条边都与权重相关联，并且存在多个生成树，我们需要找到图的最小生成树。

此外，如果存在任何重复的加权边，则该图可能具有多个最小生成树。

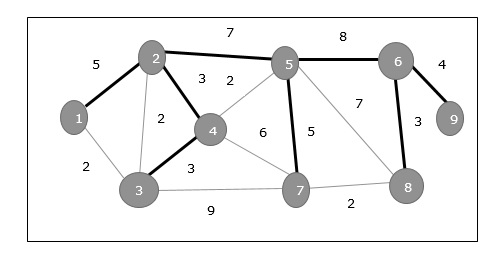
Minimum Spanning Tree

在上图中，我们显示了一个生成树，尽管它不是最小生成树。此生成树的成本为(5+7+3+3+5+8+3+4)=38。

最短路径

图中的最短路径定义为从一个顶点到另一个顶点的最小成本路线。这在加权有向图中最常见，但也适用于无向图。

在图中寻找最短路径的一个常见实际应用是地图导航。借助各种最短路径算法，目的地被视为图的顶点，路线被视为边，这使得导航更加轻松便捷。两种常用的最短路径算法是：

  • 迪杰斯特拉最短路径算法 (Dijkstra's Shortest Path Algorithm)

  • 贝尔曼-福特最短路径算法 (Bellman-Ford's Shortest Path Algorithm)

示例

以下是该操作在各种编程语言中的实现：

C语言 C++ Java Python
#include <stdio.h>
#include <stdlib.h>
#include <stdlib.h>
#define V 5 

// Maximum number of vertices in the graph
struct graph { 
   
   // declaring graph data structure
   struct vertex *point[V];
};
struct vertex { 
   
   // declaring vertices
   int end;
   struct vertex *next;
};
struct Edge { 
   
   // declaring edges
   int end, start;
};
struct graph *create_graph (struct Edge edges[], int x){
   int i;
   struct graph *graph = (struct graph *) malloc (sizeof (struct graph));
   for (i = 0; i < V; i++) {
      graph->point[i] = NULL;
   }
   for (i = 0; i < x; i++) {
      int start = edges[i].start;
      int end = edges[i].end;
      struct vertex *v = (struct vertex *) malloc (sizeof (struct vertex));
      v->end = end;
      v->next = graph->point[start];
      graph->point[start] = v;
   }
   return graph;
}
int main (){
   struct Edge edges[] = { {0, 1}, {0, 2}, {0, 3}, {1, 2}, {1, 4}, {2, 4}, {2, 3}, {3, 1} };
   int n = sizeof (edges) / sizeof (edges[0]);
   struct graph *graph = create_graph (edges, n);
   printf("The graph created is: ");
   for (int i = 0; i < V; i++) {
      struct vertex *ptr = graph->point[i];
      while (ptr != NULL) {
         printf ("(%d -> %d)\t", i, ptr->end);
         ptr = ptr->next;
      }
      printf ("\n");
   }
   return 0;
}

输出

The graph created is:
(1 -> 3)	(1 -> 0)	
(2 -> 1)	(2 -> 0)	
(3 -> 2)	(3 -> 0)	
(4 -> 2)	(4 -> 1)	

#include <bits/stdc++.h>
using namespace std;
#define V 5 

// Maximum number of vertices in the graph
struct graph { 
   
   // declaring graph data structure
   struct vertex *point[V];
};
struct vertex { 
   
   // declaring vertices
   int end;
   struct vertex *next;
};
struct Edge { 
   
   // declaring edges
   int end, start;
};
struct graph *create_graph (struct Edge edges[], int x){
   int i;
   struct graph *graph = (struct graph *) malloc (sizeof (struct graph));
   for (i = 0; i < V; i++) {
      graph->point[i] = NULL;
   }
   for (i = 0; i < x; i++) {
      int start = edges[i].start;
      int end = edges[i].end;
      struct vertex *v = (struct vertex *) malloc (sizeof (struct vertex));
      v->end = end;
      v->next = graph->point[start];
      graph->point[start] = v;
   }
   return graph;
}
int main (){
   struct Edge edges[] = { {0, 1}, {0, 2}, {0, 3}, {1, 2}, {1, 4}, {2, 4}, {2, 3}, {3, 1} };
   int n = sizeof (edges) / sizeof (edges[0]);
   struct graph *graph = create_graph (edges, n);
   int i;
   cout<<"The graph created is: ";
   for (i = 0; i < V; i++) {
      struct vertex *ptr = graph->point[i];
      while (ptr != NULL) {
         cout << "(" << i << " -> " << ptr->end << ")\t";
         ptr = ptr->next;
      }
      cout << endl;
   }
   return 0;
}

输出

The graph created is: 
(1 -> 3)	(1 -> 0)	
(2 -> 1)	(2 -> 0)	
(3 -> 2)	(3 -> 0)	
(4 -> 2)	(4 -> 1)

import java.util.*;

//class to store edges of the graph
class Edge {   
   int src, dest;
   Edge(int src, int dest) {
      this.src = src;
      this.dest = dest;
   }
}

// Graph class
public class Graph {
   
   // node of adjacency list
   static class vertex {
      int v;
      vertex(int v) {
        this.v = v;
      }
   };
   // define adjacency list to represent the graph
   List<List<vertex>> adj_list = new ArrayList<>();
   
   //Graph Constructor
   public Graph(List<Edge> edges){
      
      // adjacency list memory allocation
      for (int i = 0; i < edges.size(); i++)
      adj_list.add(i, new ArrayList<>());
      
      // add edges to the graph
      for (Edge e : edges){
        
        // allocate new node in adjacency List from src to dest
        adj_list.get(e.src).add(new vertex(e.dest));
      }
   }
   public static void main (String[] args) {
      
      // define edges of the graph
      List<Edge> edges = Arrays.asList(new Edge(0, 1),new Edge(0, 2),
      new Edge(0, 3),new Edge(1, 2), new Edge(1, 4),
      new Edge(2, 4), new Edge(2, 3),new Edge(3, 1));
      
      // call graph class Constructor to construct a graph
      Graph graph = new Graph(edges);
      
      // print the graph as an adjacency list
      int src = 0;
      int lsize = graph.adj_list.size();
      System.out.println("The graph created is: ");
      while (src < lsize) {
      
         //traverse through the adjacency list and print the edges
         for (vertex edge : graph.adj_list.get(src)) {
            System.out.print(src + " -> " + edge.v + "\t");
         }
         System.out.println();
         src++;
      }
   }
}

输出

The graph created is: 
0 -> 1	0 -> 2	0 -> 3	
1 -> 2	1 -> 4	
2 -> 4	2 -> 3	
3 -> 1

#Python code for Graph Data Struture
V = 5
#Maximum number of vertices in th graph
#Declaring vertices
class Vertex:
    def __init__(self, end):
        self.end = end
        self.next = None
#Declaring Edges
class Edge:
    def __init__(self, start, end):
        self.start = start
        self.end = end
#Declaring graph data structure
class Graph:
    def __init__(self):
        self.point = [None] * V
def create_graph(edges, x):
    graph = Graph()
    for i in range(V):
        graph.point[i] = None
    for i in range(x):
        start = edges[i].start
        end = edges[i].end
        v = Vertex(end)
        v.next = graph.point[start]
        graph.point[start] = v
    return graph
edges = [Edge(0, 1), Edge(0, 2), Edge(0, 3), Edge(1, 2), Edge(1, 4), Edge(2, 4), Edge(2, 3), Edge(3, 1)]
n = len(edges)
graph = create_graph(edges, n)
#Range
print("The graph created is: ")
for i in range(V):
    ptr = graph.point[i]
    while ptr is not None:
        print("({} -> {})".format(i, ptr.end), end="\t")
        ptr = ptr.next
    print()

输出

The graph created is: 
(0 -> 3)	(0 -> 2)	(0 -> 1)	
(1 -> 4)	(1 -> 2)	
(2 -> 3)	(2 -> 4)	
(3 -> 1)
打印页面
上一页
下一页
广告