数据结构 - 渐近分析

---

---

渐近分析

算法的渐近分析是指定义其运行时间性能的数学基础/框架。使用渐近分析，我们可以很好地得出算法的最佳情况、平均情况和最坏情况。

渐近分析是输入相关的，即如果算法没有输入，则认为其在常数时间内完成。除“输入”外，所有其他因素都被认为是常数。

渐近分析是指用数学计算单位计算任何操作的运行时间。例如，一个操作的运行时间计算为f(n)，而另一个操作的运行时间计算为g(n²)。这意味着第一个操作的运行时间将随着n的增加而线性增加，而第二个操作的运行时间将随着n的增加而呈指数增加。类似地，如果n非常小，则两个操作的运行时间将大致相同。

通常，算法所需的时间分为三种类型：

• 最佳情况 - 程序执行所需的最小时间。

• 平均情况 - 程序执行所需的平均时间。

• 最坏情况 - 程序执行所需的最多时间。

渐近记号

算法的执行时间取决于指令集、处理器速度、磁盘I/O速度等。因此，我们渐近地估计算法的效率。

算法的时间函数用T(n)表示，其中n是输入大小。

不同类型的渐近记号用于表示算法的复杂性。以下渐近记号用于计算算法的运行时间复杂性。

• O - 大O记号

• Ω - 大Ω记号

• θ - 大θ记号

• o - 小o记号

• ω - 小ω记号

大O，O：渐近上界

记号Ο(n)是表示算法运行时间上界的正式方法。是最常用的记号。它衡量最坏情况时间复杂度或算法可能完成所需的最长时间。

如果存在正整数n的值为n₀和正常数c，则函数f(n)可以表示为g(n)的阶，即O(g(n))，使得：

$f(n)\leqslant c.g(n)$ 对于所有情况下的$n > n_{0}$

因此，函数g(n)是函数f(n)的上界，因为g(n)的增长速度快于f(n)。

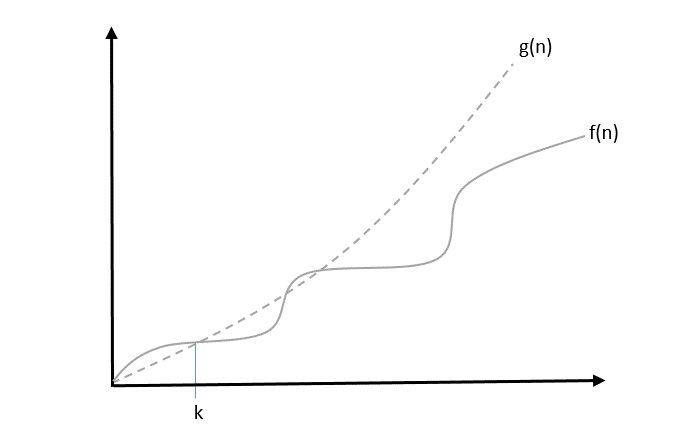
示例

让我们考虑一个给定的函数，$f(n) = 4.n^3 + 10.n^2 + 5.n + 1$

考虑$g(n) = n^3$，

$f(n)\leqslant 5.g(n)$ 对于所有$n > 2$的值

因此，f(n)的复杂度可以表示为$O(g(n))$，即$O(n^3)$

大Ω，Ω：渐近下界

记号Ω(n)是表示算法运行时间下界的正式方法。它衡量最佳情况时间复杂度或算法可能完成所需的最短时间。

当存在常数c使得$f(n)\geqslant c.g(n)$对于所有足够大的n值成立时，我们说$f(n) = \Omega (g(n))$。这里n是正整数。这意味着函数g是函数f的下界；在某个n值之后，f永远不会低于g。

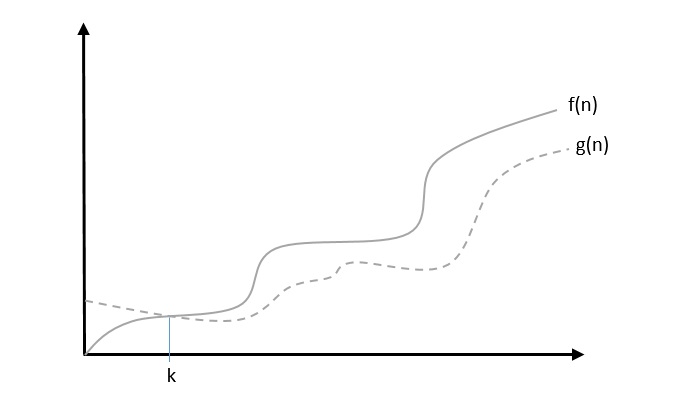
示例

让我们考虑一个给定的函数，$f(n) = 4.n^3 + 10.n^2 + 5.n + 1$。

考虑$g(n) = n^3$，$f(n)\geqslant 4.g(n)$对于所有$n > 0$的值。

因此，f(n)的复杂度可以表示为$\Omega (g(n))$，即$\Omega (n^3)$

θ，θ：渐近紧界

记号θ(n)是表示算法运行时间上下界的正式方法。有些人可能会将θ记号误认为是平均情况时间复杂度；虽然大θ记号可以几乎准确地用于描述平均情况，但也可以使用其他记号。

当存在常数c₁和c₂使得$c_{1}.g(n) \leqslant f(n) \leqslant c_{2}.g(n)$对于所有足够大的n值成立时，我们说$f(n) = \theta(g(n))$。这里n是正整数。

这意味着函数g是函数f的紧界。

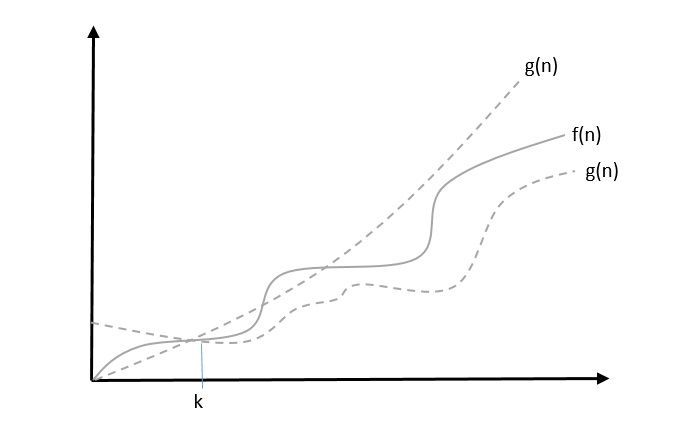
示例

让我们考虑一个给定的函数，$f(n) = 4.n^3 + 10.n^2 + 5.n + 1$

考虑$g(n) = n^3$，$4.g(n) \leqslant f(n) \leqslant 5.g(n)$对于所有较大的n值。

因此，f(n)的复杂度可以表示为$\theta (g(n))$，即$\theta (n^3)$。

小o，o

O-记号提供的渐近上界可能是也可能不是渐近紧密的。界限$2.n^2 = O(n^2)$是渐近紧密的，但界限$2.n = O(n^2)$不是。

我们使用o-记号来表示不是渐近紧密的界限。

我们正式定义o(g(n))（g(n)的小o）为集合f(n) = o(g(n))，对于任何正常数$c > 0$，都存在一个值$n_{0} > 0$，使得$0 \leqslant f(n) \leqslant c.g(n)$。

直观地说，在o-记号中，当n趋于无穷大时，函数f(n)相对于g(n)变得微不足道；也就是说，

$$\lim_{n \rightarrow \infty}\left(\frac{f(n)}{g(n)}\right) = 0$$

示例

让我们考虑相同的函数，$f(n) = 4.n^3 + 10.n^2 + 5.n + 1$

考虑$g(n) = n^{4}$，

$$\lim_{n \rightarrow \infty}\left(\frac{4.n^3 + 10.n^2 + 5.n + 1}{n^4}\right) = 0$$

因此，f(n)的复杂度可以表示为$o(g(n))$，即$o(n^4)$。

小ω，ω

我们使用ω-记号来表示不是渐近紧密的界限。然而，我们正式定义ω(g(n))（g(n)的小ω）为集合f(n) = ω(g(n))，对于任何正常数C > 0，都存在一个值$n_{0} > 0$，使得$0 \leqslant c.g(n) < f(n)$。

例如，$\frac{n^2}{2} = \omega (n)$，但$\frac{n^2}{2} \neq \omega (n^2)$。关系$f(n) = \omega (g(n))$暗示存在以下极限

$$\lim_{n \rightarrow \infty}\left(\frac{f(n)}{g(n)}\right) = \infty$$

也就是说，当n趋于无穷大时，f(n)相对于g(n)变得任意大。

示例

让我们考虑相同的函数，$f(n) = 4.n^3 + 10.n^2 + 5.n + 1$

考虑$g(n) = n^2$，

$$\lim_{n \rightarrow \infty}\left(\frac{4.n^3 + 10.n^2 + 5.n + 1}{n^2}\right) = \infty$$

因此，f(n)的复杂度可以表示为$o(g(n))$，即$\omega (n^2)$。

常用渐近记号

以下是一些常用渐近记号的列表：

常数	-	O(1)
对数	-	O(log n)
线性	-	O(n)
n log n	-	O(n log n)
平方	-	O(n2)
三次方	-	O(n3)
多项式	-	nO(1)
指数级	-	2O(n)

先验和后验分析

先验分析是指在算法运行于特定系统之前进行的分析。这种分析阶段使用某种理论模型定义函数。因此，我们只需查看算法本身，无需在具有不同内存、处理器和编译器的特定系统上运行它，即可确定算法的时间和空间复杂度。

算法的后验分析是指仅在系统运行算法之后才进行的分析。它直接依赖于系统，并且会因系统而异。

在行业中，我们无法进行后验分析，因为软件通常是为匿名用户开发的，这些用户会在与行业中存在的系统不同的系统上运行它。

在先验分析中，我们使用渐近符号来确定时间和空间复杂度的原因是，它们会因计算机而异；但是，渐近地它们是相同的。