Prim 最小生成树

Table of content

Prim 算法
示例

Prim 最小生成树算法是查找图的最小生成树的有效方法之一。最小生成树是一个子图，它以最少的边和最小的成本（分配给每条边的权重的总和）连接主图中存在的所有顶点。

该算法类似于任何最短路径算法，从一个被设置为根的顶点开始，通过确定成本最低的相邻边遍历图中的所有顶点。

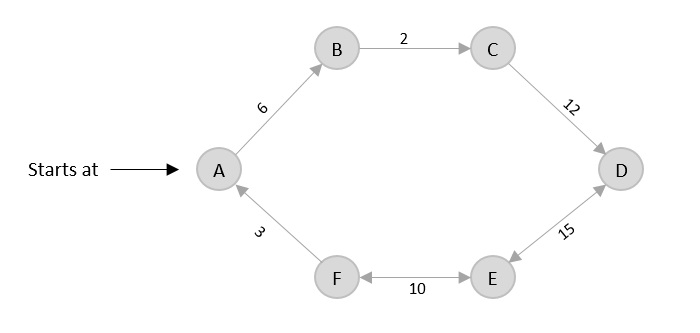
Prim 算法

要执行 Prim 算法，算法接收的输入是图 G {V, E}，其中 V 是顶点集，E 是边集，以及源顶点 S。图 G 的最小生成树作为输出获得。

算法

声明一个数组 visited[] 用于存储已访问的顶点，首先，将任意根（例如 S）添加到 visited 数组中。
检查最后一个已访问顶点的相邻顶点是否在 visited[] 数组中。
如果顶点不在 visited[] 数组中，则比较边的成本，并将成本最低的边添加到输出生成树中。
将具有最低成本边的相邻未访问顶点添加到 visited[] 数组中，并将最低成本边添加到最小生成树输出中。
步骤 2 和 4 对图中所有未访问的顶点重复执行，以获得给定图的完整最小生成树输出。
计算获得的最小生成树的成本。

示例

使用 Prim 方法（贪心算法）查找下面给定图的最小生成树，其中 S 为任意根。

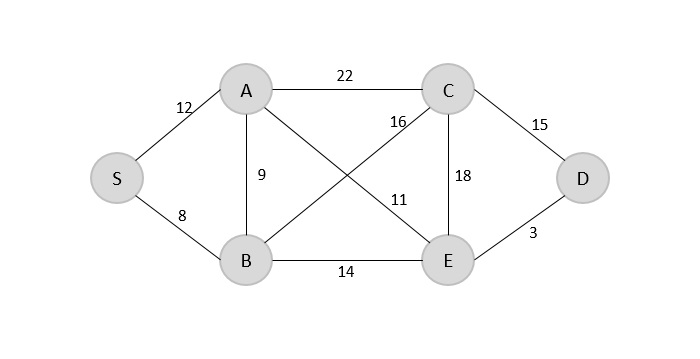
解决方案

步骤 1

创建一个 visited 数组，将所有已访问的顶点存储到其中。

V = { }

任意根被指定为 S，因此在连接到 S 的所有边中，我们需要找到成本最低的边。

S → B = 8
V = {S, B}

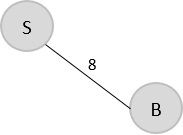
步骤 2

由于 B 是最后一个已访问的顶点，因此检查连接到顶点 B 的成本最低的边。

B → A = 9
B → C = 16
B → E = 14

因此，B → A 是添加到生成树的边。

V = {S, B, A}

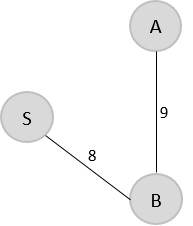
步骤 3

由于 A 是最后一个已访问的顶点，因此检查连接到顶点 A 的成本最低的边。

A → C = 22
A → B = 9
A → E = 11

但是 A → B 已经在生成树中了，检查下一个成本最低的边。因此，A → E 被添加到生成树中。

V = {S, B, A, E}

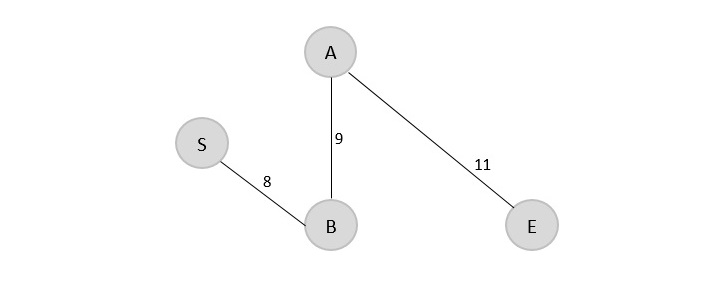
步骤 4

由于 E 是最后一个已访问的顶点，因此检查连接到顶点 E 的成本最低的边。

E → C = 18
E → D = 3

因此，E → D 被添加到生成树中。

V = {S, B, A, E, D}

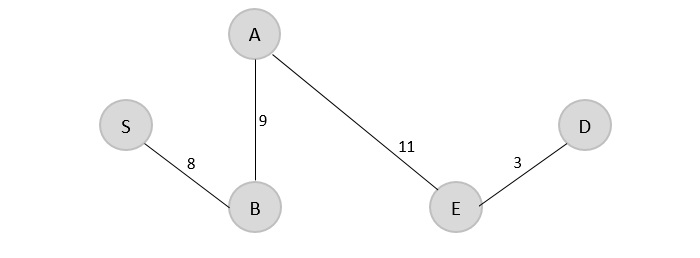
步骤 5

由于 D 是最后一个已访问的顶点，因此检查连接到顶点 D 的成本最低的边。

D → C = 15
E → D = 3

因此，D → C 被添加到生成树中。

V = {S, B, A, E, D, C}

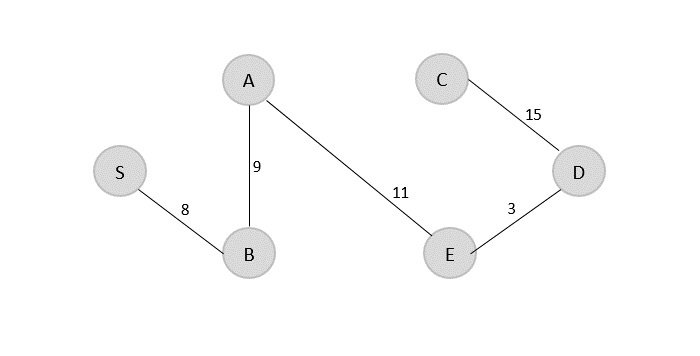
获得的最小生成树的最小成本 = 46

示例

最终程序实现了 Prim 最小生成树问题，该问题以成本邻接矩阵作为输入，并打印生成树作为输出以及最小成本。

C C++ Java Python

#include<stdio.h>
#include<stdlib.h>
#define inf 99999
#define MAX 10
int G[MAX][MAX] = {
   {0, 19, 8},
   {21, 0, 13},
   {15, 18, 0}
};
int S[MAX][MAX], n;
int prims();
int main(){
   int i, j, cost;
   n = 3;
   cost=prims();
   printf("Spanning tree:");
   for(i=0; i<n; i++) {
      printf("\n");
      for(j=0; j<n; j++)
         printf("%d\t",S[i][j]);
   }
   printf("\nMinimum cost = %d", cost);
   return 0;
}
int prims(){
   int C[MAX][MAX];
   int u, v, min_dist, dist[MAX], from[MAX];
   int visited[MAX],ne,i,min_cost,j;

   //create cost[][] matrix,spanning[][]
   for(i=0; i<n; i++)
      for(j=0; j<n; j++) {
         if(G[i][j]==0)
            C[i][j]=inf;
         else
            C[i][j]=G[i][j];
         S[i][j]=0;
      }

   //initialise visited[],distance[] and from[]
   dist[0]=0;
   visited[0]=1;
   for(i=1; i<n; i++) {
      dist[i] = C[0][i];
      from[i] = 0;
      visited[i] = 0;
   }
   min_cost = 0; //cost of spanning tree
   ne = n-1; //no. of edges to be added
   while(ne > 0) {

      //find the vertex at minimum distance from the tree
      min_dist = inf;
      for(i=1; i<n; i++)
         if(visited[i] == 0 && dist[i] < min_dist) {
            v = i;
            min_dist = dist[i];
         }
      u = from[v];

      //insert the edge in spanning tree
      S[u][v] = dist[v];
      S[v][u] = dist[v];
      ne--;
      visited[v]=1;

      //updated the distance[] array
      for(i=1; i<n; i++)
         if(visited[i] == 0 && C[i][v] < dist[i]) {
            dist[i] = C[i][v];
            from[i] = v;
         }
      min_cost = min_cost + C[u][v];
   }
   return(min_cost);
}

输出

Spanning tree:
0	0	8	
0	0	13	
8	13	0	
Minimum cost = 26

#include<iostream>
#define inf 999999
#define MAX 10
using namespace std;
int G[MAX][MAX] = {
   {0, 19, 8},
   {21, 0, 13},
   {15, 18, 0}
};
int S[MAX][MAX], n;
int prims();
int main(){
   int i, j, cost;
   n = 3;
   cost=prims();
   cout <<"Spanning tree:";
   for(i=0; i<n; i++) {
      cout << endl;
      for(j=0; j<n; j++)
         cout << S[i][j] << " ";
   }
   cout << "\nMinimum cost = " << cost;
   return 0;
}
int prims(){
   int C[MAX][MAX];
   int u, v, min_dist, dist[MAX], from[MAX];
   int visited[MAX],ne,i,min_cost,j;

   //create cost matrix and spanning tree
   for(i=0; i<n; i++)
      for(j=0; j<n; j++) {
         if(G[i][j]==0)
            C[i][j]=inf;
         else
            C[i][j]=G[i][j];
         S[i][j]=0;
      }

   //initialise visited[],distance[] and from[]
   dist[0]=0;
   visited[0]=1;
   for(i=1; i<n; i++) {
      dist[i] = C[0][i];
      from[i] = 0;
      visited[i] = 0;
   }
   min_cost = 0; //cost of spanning tree
   ne = n-1; //no. of edges to be added
   while(ne > 0) {

      //find the vertex at minimum distance from the tree
      min_dist = inf;
      for(i=1; i<n; i++)
         if(visited[i] == 0 && dist[i] < min_dist) {
            v = i;
            min_dist = dist[i];
         }
      u = from[v];

      //insert the edge in spanning tree
      S[u][v] = dist[v];
      S[v][u] = dist[v];
      ne--;
      visited[v]=1;

      //updated the distance[] array
      for(i=1; i<n; i++)
         if(visited[i] == 0 && C[i][v] < dist[i]) {
            dist[i] = C[i][v];
            from[i] = v;
         }
      min_cost = min_cost + C[u][v];
   }
   return(min_cost);
}

输出

Spanning tree:
0 0 8 
0 0 13 
8 13 0 
Minimum cost = 26

public class prims {
   static int inf = 999999;
   static int MAX = 10;
   static int G[][] = {
       {0, 19, 8},
       {21, 0, 13},
       {15, 18, 0}
   };
   static int S[][] = new int[MAX][MAX];
   static int n;
   public static void main(String args[]) {
      int i, j, cost;
      n = 3;
      cost=prims();
      System.out.print("Spanning tree: ");
      for(i=0; i<n; i++) {
         System.out.println();
         for(j=0; j<n; j++)
            System.out.print(S[i][j] + " ");
      }
      System.out.println("\nMinimum cost = " + cost);
   }
   static int prims() {
      int C[][] = new int[MAX][MAX];
      int u, v = 0, min_dist;
      int dist[] = new int[MAX];
      int from[] = new int[MAX];
      int visited[] = new int[MAX];
      int ne,i,min_cost,j;
      //create cost matrix and spanning tree
      for(i=0; i<n; i++)
         for(j=0; j<n; j++) {
            if(G[i][j]==0)
               C[i][j]=inf;
            else
               C[i][j]=G[i][j];
            S[i][j]=0;
         }
      //initialise visited[],distance[] and from[]
      dist[0]=0;
      visited[0]=1;
      for(i=1; i<n; i++) {
         dist[i] = C[0][i];
         from[i] = 0;
         visited[i] = 0;
      }
      min_cost = 0; //cost of spanning tree
      ne = n-1; //no. of edges to be added
      while(ne > 0) {
         //find the vertex at minimum distance from the tree
         min_dist = inf;
         for(i=1; i<n; i++)
            if(visited[i] == 0 && dist[i] < min_dist) {
               v = i;
               min_dist = dist[i];
            }
         u = from[v];
         //insert the edge in spanning tree
         S[u][v] = dist[v];
         S[v][u] = dist[v];
         ne--;
         visited[v]=1;
         //updated the distance[] array
         for(i=1; i<n; i++)
            if(visited[i] == 0 && C[i][v] < dist[i]) {
               dist[i] = C[i][v];
               from[i] = v;
            }
         min_cost = min_cost + C[u][v];
      }
      return(min_cost);
   }
}

输出

Spanning tree: 
0 0 8 
0 0 13 
8 13 0 
Minimum cost = 26

inf = 999999
MAX = 10
G = [
    [0, 19, 8],
    [21, 0, 13],
    [15, 18, 0]
]
S = [[0 for _ in range(MAX)] for _ in range(MAX)]
n = 3
def main():
    global n
    cost = prims()
    print("Spanning tree: ")
    for i in range(n):
        print()
        for j in range(n):
            print(S[i][j], end=" ")
    print("\nMinimum cost =", cost)
def prims():
    global n
    C = [[0 for _ in range(MAX)] for _ in range(MAX)]
    u, v = 0, 0
    min_dist = 0
    dist = [0 for _ in range(MAX)]
    from_ = [0 for _ in range(MAX)]
    visited = [0 for _ in range(MAX)]
    ne = 0
    min_cost = 0
    i = 0
    j = 0
    for i in range(n):
        for j in range(n):
            if G[i][j] == 0:
                C[i][j] = inf
            else:
                C[i][j] = G[i][j]
            S[i][j] = 0
    dist[0] = 0
    visited[0] = 1
    for i in range(1, n):
        dist[i] = C[0][i]
        from_[i] = 0
        visited[i] = 0
    min_cost = 0
    ne = n - 1
    while ne > 0:
        min_dist = inf
        for i in range(1, n):
            if visited[i] == 0 and dist[i] < min_dist:
                v = i
                min_dist = dist[i]
        u = from_[v]
        S[u][v] = dist[v]
        S[v][u] = dist[v]
        ne -= 1
        visited[v] = 1
        for i in range(n):
            if visited[i] == 0 and C[i][v] < dist[i]:
                dist[i] = C[i][v]
                from_[i] = v
        min_cost += C[u][v]
    return min_cost
#calling  the main() method
main()

输出

Spanning tree: 

0 0 8 
0 0 13 
8 13 0 
Minimum cost = 26

打印页面