随机算法

随机算法是一种与标准算法不同的设计方法，它在算法逻辑的某些部分添加了一些随机比特。它们与确定性算法不同；确定性算法遵循确定的程序，每次输入都会得到相同的输出，而随机算法每次执行都会产生不同的输出。需要注意的是，随机的不是输入，而是标准算法的逻辑。

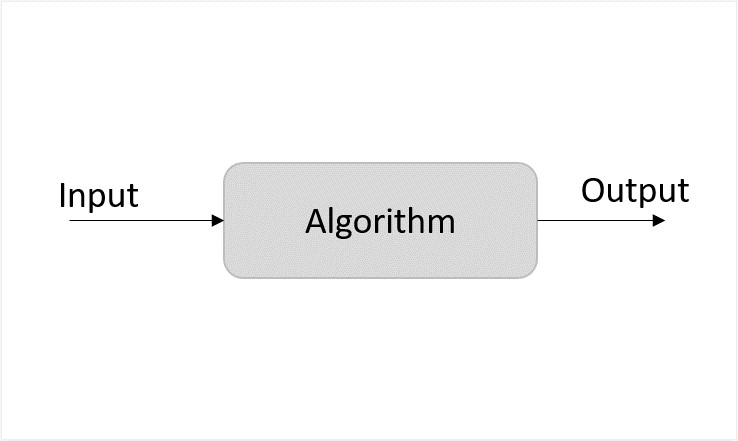
图1：确定性算法

与确定性算法不同，随机算法除了考虑输入外，还考虑逻辑中的随机比特，这些比特反过来有助于获得输出。

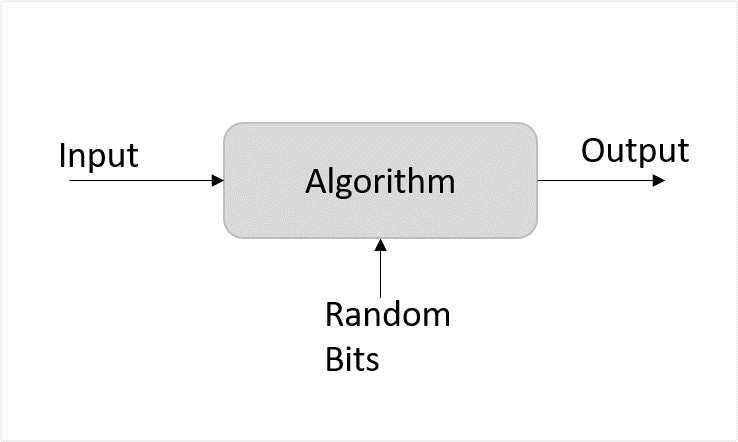
图2：随机算法

然而，也不能排除随机算法产生错误输出的可能性。因此，执行称为**放大**的过程以减少这些错误输出的可能性。放大也是一种算法，它用于多次执行随机算法的某些部分以提高正确性的概率。然而，过多的放大也会超过时间限制，使算法无效。

随机算法的分类

随机算法根据其时间约束是随机变量还是确定性值进行分类。它们以两种常见形式设计——拉斯维加斯和蒙特卡洛。

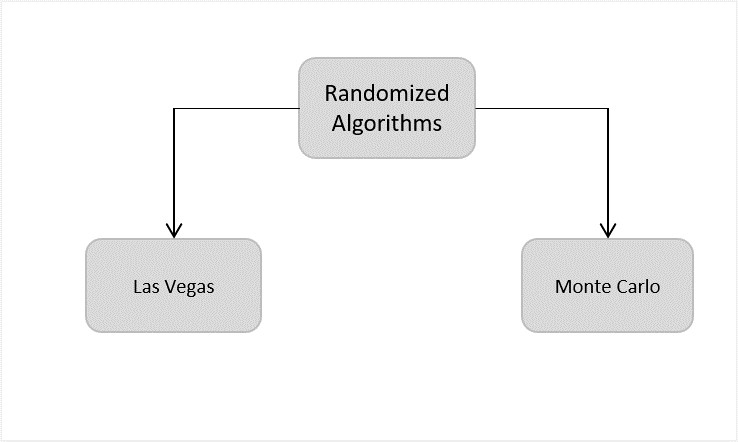
• **拉斯维加斯**——拉斯维加斯方法的随机算法永远不会给出错误的输出，这使得时间约束成为随机变量。例如，在字符串匹配算法中，拉斯维加斯算法一旦遇到错误就从头开始。这增加了正确性的概率。例如，随机快速排序算法。

• **蒙特卡罗**——蒙特卡罗方法的随机算法专注于在给定的时间约束内完成执行。因此，此方法的运行时间是确定的。例如，在字符串匹配中，如果蒙特卡罗遇到错误，它会从同一点重新启动算法。从而节省时间。例如，Karger最小割算法

随机算法的必要性

这种方法通常用于降低时间复杂度和空间复杂度。但对于添加随机性如何降低运行时间和存储内存而不是增加，可能存在一些模糊之处；我们将使用博弈论来理解这一点。

博弈论与随机算法

博弈论的基本思想实际上提供了一些模型，这些模型有助于理解游戏中的决策者如何相互作用。这些博弈论模型使用假设来确定游戏中参与者的决策结构。这些理论模型做出的流行假设是，参与者都是理性的，并且会考虑对手在特定游戏情况下会做出什么决定。我们将把这个理论应用于随机算法。

零和博弈

零和博弈是博弈论的数学表示。它有两个参与者，结果对一个参与者是收益，而对另一个参与者是等值的损失。因此，净改进是两个参与者状态的总和，总和为零。

随机算法基于设计一种算法的零和博弈，该算法对所有输入都具有最低的时间复杂度。游戏中有两个参与者；一个设计算法，另一个为算法提供输入。玩家二需要以这样一种方式提供输入，即它将产生最坏的时间复杂度以赢得游戏。而玩家一需要设计一种算法，该算法执行任何给定输入所需的时间最短。

例如，考虑快速排序算法，其中主算法从选择枢轴元素开始。但是，如果零和博弈中的玩家选择排序列表作为输入，则标准算法会提供最坏情况下的时间复杂度。因此，随机化枢轴选择将比最坏时间复杂度更快地执行算法。但是，即使算法随机选择第一个元素作为枢轴并获得最坏的时间复杂度，使用相同的输入再次执行它也会解决问题，因为它这次会选择另一个枢轴。

另一方面，对于像归并排序这样的算法，时间复杂度不依赖于输入；即使算法是随机的，时间复杂度也会保持不变。因此，**随机化仅应用于复杂度取决于输入的算法**。

示例

随机算法的一些流行示例是：

• 随机快速排序算法

• Karger最小割算法

• Fisher-Yates洗牌算法

• 子集和问题