旅行商问题（贪心算法）

Table of content

旅行推销员算法
示例

旅行商问题是一个图计算问题，其中推销员需要只访问一次列表中的所有城市（用图中的节点表示），并且已知所有这些城市之间的距离（用图中的边表示）。这个问题需要找到的解是推销员访问所有城市并返回原城市的最短路线。

如果您查看下面的图表，假设推销员从顶点“a”开始，他们需要遍历所有剩余的顶点b、c、d、e、f并返回“a”，同时确保成本最小。

有各种方法可以找到旅行商问题的解决方案：朴素方法、贪心方法、动态规划方法等。在本教程中，我们将学习如何使用贪心方法解决旅行商问题。

旅行推销员算法

正如贪心方法的定义所述，我们需要找到局部最优解来找出全局最优解。算法的输入是图G{V, E}，其中V是顶点集，E是边集。从一个顶点开始返回同一顶点的图G的最短路径作为输出获得。

算法

旅行商问题将图G{V, E}作为输入，并声明另一个图作为输出（例如G'），该图将记录推销员从一个节点到另一个节点的路径。
该算法首先将输入图G中的所有边从最短距离到最长距离排序。
选择的第一个边是最短距离的边，两个顶点之一（例如A和B）是起点节点（例如A）。
然后，在除起点节点（B）之外的节点的相邻边中，找到成本最低的边并将其添加到输出图中。
继续使用其他节点进行此过程，确保输出图中没有循环，并且路径返回到起点节点A。
但是，如果问题中提到了起点，则解决方案必须始终从该节点开始。让我们看一些示例问题以更好地理解这一点。

示例

考虑以下具有六个城市及其之间距离的图 -

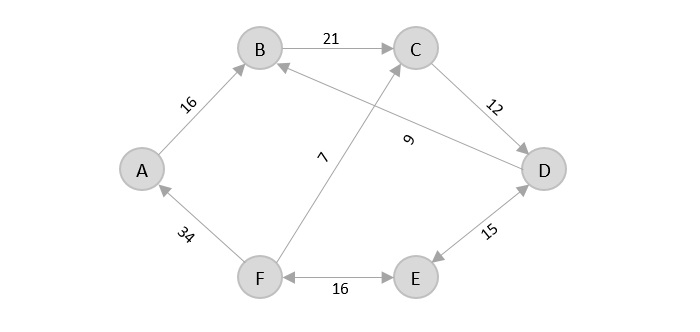
从给定的图中，由于起点已提及，因此解决方案必须始终从该节点开始。在从A引出的边中，A→B距离最短。

然后，B→C具有最短且唯一的边，因此将其包含在输出图中。

C→D之间只有一条边，因此将其添加到输出图中。

D有两条外向边。即使D→B的距离小于D→E，B也已经访问过一次，如果添加到输出图中，它将形成一个循环。因此，D→E被添加到输出图中。

从e只有一条边，即E→F。因此，它被添加到输出图中。

同样，即使F→C的距离小于F→A，为了避免形成循环并且C已经访问过一次，F→A被添加到输出图中。

从A开始并以A结束的最短路径是A→B→C→D→E→F→A

路径的成本是：16 + 21 + 12 + 15 + 16 + 34 = 114。

即使从其他节点开始可以降低路径成本，但问题并没有就此提出。

示例

下面给出了使用贪心方法的旅行商问题的完整实现 -

C C++ Java Python

Open Compiler

#include <stdio.h>
int tsp_g[10][10] = {
   {12, 30, 33, 10, 45},
   {56, 22, 9, 15, 18},
   {29, 13, 8, 5, 12},
   {33, 28, 16, 10, 3},
   {1, 4, 30, 24, 20}
};
int visited[10], n, cost = 0;

/* creating a function to generate the shortest path */
void travellingsalesman(int c){
   int k, adj_vertex = 999;
   int min = 999;
   
   /* marking the vertices visited in an assigned array */
   visited[c] = 1;
   
   /* displaying the shortest path */
   printf("%d ", c + 1);
   
   /* checking the minimum cost edge in the graph */
   for(k = 0; k < n; k++) {
      if((tsp_g[c][k] != 0) && (visited[k] == 0)) {
         if(tsp_g[c][k] < min) {
            min = tsp_g[c][k];
            adj_vertex = k;
         }
      }
   }
   if(min != 999) {
      cost = cost + min;
   }
   if(adj_vertex == 999) {
      adj_vertex = 0;
      printf("%d", adj_vertex + 1);
      cost = cost + tsp_g[c][adj_vertex];
      return;
   }
   travellingsalesman(adj_vertex);
}

/* main function */
int main(){
   int i, j;
   n = 5;
   for(i = 0; i < n; i++) {
      visited[i] = 0;
   }
   printf("Shortest Path: ");
   travellingsalesman(0);
   printf("\nMinimum Cost: ");
   printf("%d\n", cost);
   return 0;
}

输出

Shortest Path: 1 4 5 2 3 1
Minimum Cost: 55

Open Compiler

#include <iostream>
using namespace std;
int tsp_g[10][10] = {{12, 30, 33, 10, 45},
{56, 22, 9, 15, 18},
{29, 13, 8, 5, 12},
{33, 28, 16, 10, 3},
{1, 4, 30, 24, 20}
};
int visited[10], n, cost = 0;

/* creating a function to generate the shortest path */
void travellingsalesman(int c){
   int k, adj_vertex = 999;
   int min = 999;
   
   /* marking the vertices visited in an assigned array */
   visited[c] = 1;
   
   /* displaying the shortest path */
   cout<<c + 1<<" ";
   
   /* checking the minimum cost edge in the graph */
   for(k = 0; k < n; k++) {
      if((tsp_g[c][k] != 0) && (visited[k] == 0)) {
         if(tsp_g[c][k] < min) {
            min = tsp_g[c][k];
               adj_vertex = k;
         }
      }
   }
   if(min != 999) {
      cost = cost + min;
   }
   if(adj_vertex == 999) {
      adj_vertex = 0;
      cout<<adj_vertex + 1;
      cost = cost + tsp_g[c][adj_vertex];
      return;
   }
   travellingsalesman(adj_vertex);
}

/* main function */
int main(){
   int i, j;
   n = 5;
   for(i = 0; i < n; i++) {
      visited[i] = 0;
   }
   cout<<"Shortest Path: ";
   travellingsalesman(0);
   cout<<"\nMinimum Cost: ";
   cout<<cost;
   return 0;
}

输出

Shortest Path: 1 4 5 2 3 1
Minimum Cost: 55

Open Compiler

import java.util.*;
public class Main {
    static int[][] tsp_g = {
	   {12, 30, 33, 10, 45},
       {56, 22, 9, 15, 18},
       {29, 13, 8, 5, 12},
       {33, 28, 16, 10, 3},
       {1, 4, 30, 24, 20}};
    static int[] visited;
    static int n, cost;
    public static void travellingsalesman(int c) {
        int k, adj_vertex = 999;
        int min = 999;
        visited[c] = 1;
        System.out.print((c + 1) + " ");
        for (k = 0; k < n; k++) {
            if ((tsp_g[c][k] != 0) && (visited[k] == 0)) {
                if (tsp_g[c][k] < min) {
                    min = tsp_g[c][k];
					adj_vertex = k;
                }
            }
        }
        if (min != 999) {
            cost = cost + min;
        }
        if (adj_vertex == 999) {
            adj_vertex = 0;
            System.out.print((adj_vertex + 1));
            cost = cost + tsp_g[c][adj_vertex];
            return;
        }
        travellingsalesman(adj_vertex);
    }
    public static void main(String[] args) {
        int i, j;
        n = 5;
        visited = new int[n];
        Arrays.fill(visited, 0);
        System.out.print("Shortest Path: ");
        travellingsalesman(0);
        System.out.print("\nMinimum Cost: ");
        System.out.print(cost);
    }
}

输出

Shortest Path: 1 4 5 2 3 1
Minimum Cost: 55

Open Compiler

import numpy as np
def travellingsalesman(c):
    global cost
    adj_vertex = 999
    min_val = 999
    visited[c] = 1
    print((c + 1), end=" ")
    for k in range(n):
        if (tsp_g[c][k] != 0) and (visited[k] == 0):
            if tsp_g[c][k] < min_val:
                min_val = tsp_g[c][k]
                adj_vertex = k
    if min_val != 999:
        cost = cost + min_val
    if adj_vertex == 999:
        adj_vertex = 0
        print((adj_vertex + 1), end=" ")
        cost = cost + tsp_g[c][adj_vertex]
        return
    travellingsalesman(adj_vertex)
n = 5
cost = 0
visited = np.zeros(n, dtype=int)
tsp_g = np.array([[12, 30, 33, 10, 45],
                  [56, 22, 9, 15, 18],
                  [29, 13, 8, 5, 12],
                  [33, 28, 16, 10, 3],
                  [1, 4, 30, 24, 20]])
print("Shortest Path:", end=" ")
travellingsalesman(0)
print()
print("Minimum Cost:", end=" ")
print(cost)

输出

Shortest Path: 1 4 5 2 3 1 
Minimum Cost: 55

打印页面