线性搜索算法

线性搜索是一种顺序搜索算法。在这种方法中，遍历输入数组中的每个元素并将其与要查找的关键元素进行比较。如果在数组中找到匹配项，则搜索被认为是成功的；如果没有找到匹配项，则搜索被认为是不成功的，并给出最坏情况下的时间复杂度。

例如，在给定的动画图中，我们正在搜索元素 33。因此，线性搜索方法从第一个元素开始顺序搜索，直到找到匹配项。这返回一个成功的搜索。

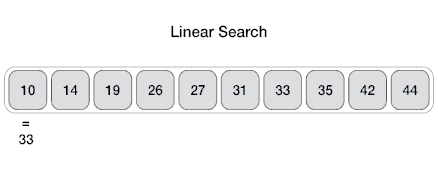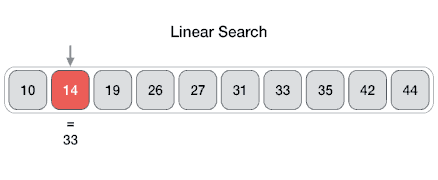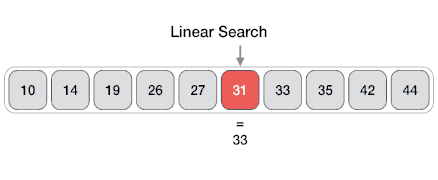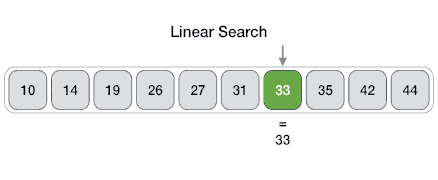
在同一张图中，如果我们必须搜索元素 46，则它会返回一个不成功的搜索，因为 46 不存在于输入中。

线性搜索算法

线性搜索的算法相对简单。该过程从要搜索的输入数组的第一个索引开始。

步骤 1 - 从输入数组的第 0 个索引开始，将关键值与第 0 个索引中存在的值进行比较。

步骤 2 - 如果值与键匹配，则返回找到该值的位置。

步骤 3 - 如果值与键不匹配，则比较数组中的下一个元素。

步骤 4 - 重复步骤 3，直到找到匹配项。返回找到匹配项的位置。

步骤 5 - 如果搜索不成功，则打印该元素不存在于数组中并退出程序。

伪代码

procedure linear_search (list, value)
   for each item in the list
      if match item == value
         return the item's location
      end if
   end for
end procedure

分析

线性搜索依次遍历每个元素，因此，最佳情况是在第一次迭代中找到元素。最佳情况下的时间复杂度为O(1)。

但是，线性搜索方法的最坏情况将是不成功的搜索，它在数组中找不到关键值，它执行 n 次迭代。因此，线性搜索算法的最坏情况下的时间复杂度为O(n)。

示例

让我们看看使用线性搜索方法在数组中逐步搜索关键元素（例如 47）的过程。

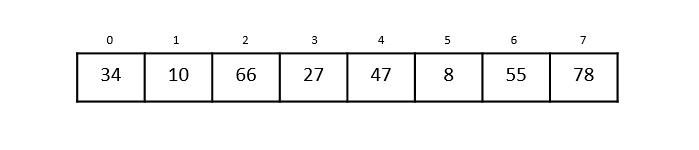
步骤 1

线性搜索从第 0 个索引开始。将关键元素与第 0 个索引中的值 34 进行比较。

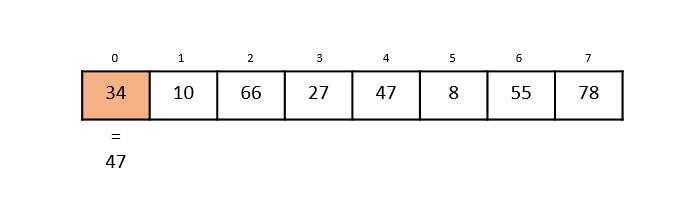
但是，47 ≠ 34。所以它移动到下一个元素。

步骤 2

现在，关键元素与数组中第 1 个索引的值进行比较。

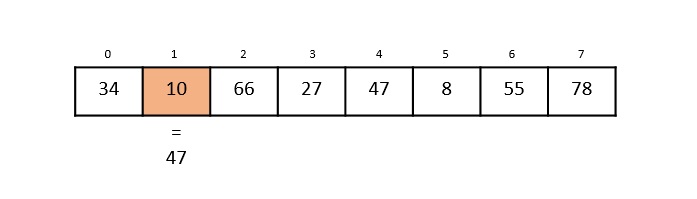
仍然，47 ≠ 10，使算法继续进行另一次迭代。

步骤 3

将下一个元素 66 与 47 进行比较。它们都不匹配，因此算法继续比较后续元素。

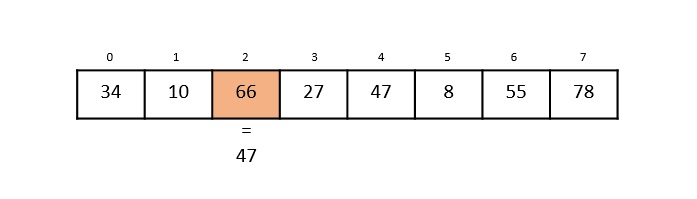
步骤 4

现在，将第 3 个索引中的元素 27 与关键值 47 进行比较。它们不相等，因此算法被推送到检查下一个元素。

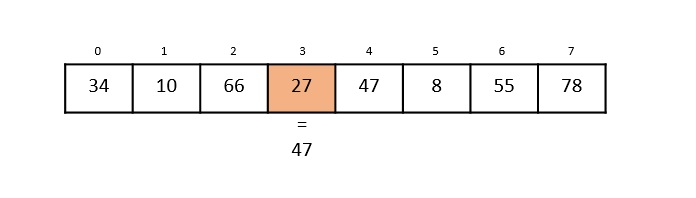
步骤 5

将数组中第 4 个索引中的元素 47 与关键值 47 进行比较。发现这两个元素匹配。现在，返回 47 所在的位置，即 4。

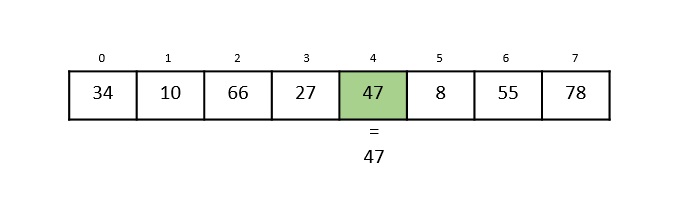
获得的输出为“在第 4 个索引处找到元素”。

实现

在本教程中，可以看出线性搜索程序在四种编程语言中实现。该函数将输入的元素与关键值进行比较，并返回键在数组中的位置，或者如果键不存在于数组中，则返回不成功的搜索提示。

#include <stdio.h>
void linear_search(int a[], int n, int key){
   int i, count = 0;
   for(i = 0; i < n; i++) {
      if(a[i] == key) { // compares each element of the array
         printf("The element is found at %d position\n", i+1);
         count = count + 1;
      }
   }
   if(count == 0) // for unsuccessful search
      printf("The element is not present in the array\n");
}
int main(){
   int i, n, key;
   n = 6;
   int a[10] = {12, 44, 32, 18, 4, 10};
   key = 18;
   linear_search(a, n, key);
   key = 23;
   linear_search(a, n, key);
   return 0;
}

The element is found at 4 position
The element is not present in the array

#include <iostream>
using namespace std;
void linear_search(int a[], int n, int key){
   int i, count = 0;
   for(i = 0; i < n; i++) {
     if(a[i] == key) { // compares each element of the array
       cout << "The element is found at position " << i+1 <<endl;
       count = count + 1;
     }
   }
   if(count == 0) // for unsuccessful search
     cout << "The element is not present in the array" <<endl;
}
int main(){
   int i, n, key;
   n = 6;
   int a[10] = {12, 44, 32, 18, 4, 10};
   key = 18;
   linear_search(a, n, key);
   key = 23;
   linear_search(a, n, key);
   return 0;
}

The element is found at position 4
The element is not present in the array

import java.io.*;
import java.util.*;
public class LinearSearch {
   static void linear_search(int a[], int n, int key) {
      int i, count = 0;
      for(i = 0; i < n; i++) {
         if(a[i] == key) { // compares each element of the array
            System.out.println("The element is found at position " + (i+1));
            count = count + 1;
         }
      }
      if(count == 0) // for unsuccessful search
         System.out.println("The element is not present in the array");
      }
   public static void main(String args[]) {
      int i, n, key;
      n = 6;
      int a[] = {12, 44, 32, 18, 4, 10, 66};
      key = 10;
      linear_search(a, n, key);
      key = 54;
      linear_search(a, n, key);
   }
}

The element is found at position 6
The element is not present in the array

def linear_search(a, n, key):
   count = 0
   for i in range(n):
      if(a[i] == key):
         print("The element is found at position", (i+1))
         count = count + 1
   if(count == 0):
      print("The element is not present in the array")

a = [14, 56, 77, 32, 84, 9, 10]
n = len(a)
key = 32
linear_search(a, n, key)
key = 3
linear_search(a, n, key)

The element is found at position 4
The element is not present in the array