弗洛伊德-沃歇尔算法

弗洛伊德-沃歇尔算法是一种图算法，用于查找加权图中所有顶点之间的最短路径。该算法不同于其他最短路径算法；简单来说，该算法使用图中的每个顶点作为枢纽，检查它是否提供了从一点到另一点的最快路径。

弗洛伊德-沃歇尔算法适用于有向和无向加权图，除非这些图不包含任何负环。负环是指图中所有边的总和不能导致负数。

由于该算法处理重叠子问题——由顶点作为枢纽找到的路径被存储以解决后续步骤——因此它使用动态规划方法。

弗洛伊德-沃歇尔算法是所有对最短路径算法中的一种方法，它使用图的邻接矩阵表示来求解。

Floyd-Warshall算法

考虑一个图，G = {V, E}，其中V是图中所有顶点的集合，E是图中所有边的集合。图G以邻接矩阵A的形式表示，该矩阵包含连接两个顶点的每条边的所有权重。

算法

步骤1 - 构造一个邻接矩阵A，其中包含图中所有边的权重。如果两个顶点之间没有路径，则将值标记为∞。

步骤2 - 从A派生另一个邻接矩阵A₁，在A₁中保持原始邻接矩阵的第1行和第1列不变。对于其余的值，例如A₁[i,j]，如果A[i,j]>A[i,k]+A[k,j]，则用A[i,k]+A[k,j]替换A₁[i,j]。否则，不要更改值。在此步骤中，k = 1（第一个顶点作为枢纽）。

步骤3 - 通过为每个枢纽顶点更改k值，对图中的所有顶点重复步骤2，直到获得最终矩阵。

步骤4 - 获得的最终邻接矩阵是包含所有最短路径的最终解。

伪代码

Floyd-Warshall(w, n){ // w: weights, n: number of vertices
   for i = 1 to n do // initialize, D (0) = [wij]
      for j = 1 to n do{
         d[i, j] = w[i, j];
      }
      for k = 1 to n do // Compute D (k) from D (k-1)
         for i = 1 to n do
            for j = 1 to n do
               if (d[i, k] + d[k, j] < d[i, j]){
                  d[i, j] = d[i, k] + d[k, j];
               }
      return d[1..n, 1..n];
}

示例

考虑以下有向加权图G = {V, E}。使用弗洛伊德-沃歇尔算法查找图中所有顶点之间的最短路径。

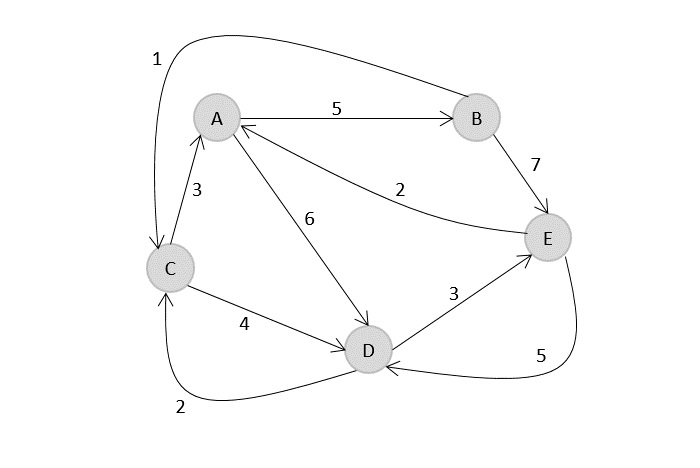
解答

步骤1

构造一个邻接矩阵A，其中所有距离作为值。

$$A=\begin{matrix} 0 & 5& \infty & 6& \infty \\ \infty & 0& 1& \infty& 7\\ 3 & \infty& 0& 4& \infty\\ \infty & \infty& 2& 0& 3\\ 2& \infty& \infty& 5& 0\\ \end{matrix}$$

步骤2

将上述邻接矩阵作为输入，通过仅保持第一行和第一列不变来派生另一个矩阵A₀。取k = 1，并用A[i,k]+A[k,j]替换所有其他值。

$$A=\begin{matrix} 0 & 5& \infty & 6& \infty \\ \infty & & & & \\ 3& & & & \\ \infty& & & & \\ 2& & & & \\ \end{matrix}$$

$$A_{1}=\begin{matrix} 0 & 5& \infty & 6& \infty \\ \infty & 0& 1& \infty& 7\\ 3 & 8& 0& 4& \infty\\ \infty & \infty& 2& 0& 3\\ 2& 7& \infty& 5& 0\\ \end{matrix}$$

步骤3

将上述邻接矩阵作为输入，通过仅保持第一行和第一列不变来派生另一个矩阵A₀。取k = 1，并用A[i,k]+A[k,j]替换所有其他值。

$$A_{2}=\begin{matrix} & 5& & & \\ \infty & 0& 1& \infty& 7\\ & 8& & & \\ & \infty& & & \\ & 7& & & \\ \end{matrix}$$

$$A_{2}=\begin{matrix} 0 & 5& 6& 6& 12 \\ \infty & 0& 1& \infty& 7\\ 3 & 8& 0& 4& 15\\ \infty & \infty& 2& 0& 3\\ 2 & 7& 8& 5& 0 \\ \end{matrix}$$

步骤4

将上述邻接矩阵作为输入，通过仅保持第一行和第一列不变来派生另一个矩阵A₀。取k = 1，并用A[i,k]+A[k,j]替换所有其他值。

$$A_{3}=\begin{matrix} & & 6& & \\ & & 1& & \\ 3 & 8& 0& 4& 15\\ & & 2& & \\ & & 8& & \\ \end{matrix}$$

$$A_{3}=\begin{matrix} 0 & 5& 6& 6& 12 \\ 4 & 0& 1& 5& 7\\ 3 & 8& 0& 4& 15\\ 5 & 10& 2& 0& 3\\ 2 & 7& 8& 5& 0 \\ \end{matrix}$$

步骤5

将上述邻接矩阵作为输入，通过仅保持第一行和第一列不变来派生另一个矩阵A₀。取k = 1，并用A[i,k]+A[k,j]替换所有其他值。

$$A_{4}=\begin{matrix} & & & 6& \\ & & & 5& \\ & & & 4& \\ 5 & 10& 2& 0& 3\\ & & & 5& \\ \end{matrix}$$

$$A_{4}=\begin{matrix} 0 & 5& 6& 6& 9 \\ 4 & 0& 1& 5& 7\\ 3 & 8& 0& 4& 7\\ 5 & 10& 2& 0& 3\\ 2 & 7& 7& 5& 0 \\ \end{matrix}$$

步骤6

将上述邻接矩阵作为输入，通过仅保持第一行和第一列不变来派生另一个矩阵A₀。取k = 1，并用A[i,k]+A[k,j]替换所有其他值。

$$A_{5}=\begin{matrix} & & & & 9 \\ & & & & 7\\ & & & & 7\\ & & & & 3\\ 2 & 7& 7& 5& 0 \\ \end{matrix}$$

$$A_{5}=\begin{matrix} 0 & 5& 6& 6& 9 \\ 4 & 0& 1& 5& 7\\ 3 & 8& 0& 4& 7\\ 5 & 10& 2& 0& 3\\ 2 & 7& 7& 5& 0 \\ \end{matrix}$$

分析

从上面的伪代码可以看出，弗洛伊德-沃歇尔算法使用三个for循环来查找图中所有顶点对之间的最短距离。因此，弗洛伊德-沃歇尔算法的时间复杂度为O(n³)，其中'n'是图中顶点的数量。该算法的空间复杂度为O(n²)。

实现

以下是使用成本邻接矩阵查找图中最短路径的弗洛伊德-沃歇尔算法的实现 -

#include <stdio.h>
void floyds(int b[3][3]) {
   int i, j, k;
   for (k = 0; k < 3; k++) {
      for (i = 0; i < 3; i++) {
         for (j = 0; j < 3; j++) {
            if ((b[i][k] * b[k][j] != 0) && (i != j)) {
               if ((b[i][k] + b[k][j] < b[i][j]) || (b[i][j] == 0)) {
                  b[i][j] = b[i][k] + b[k][j];
               }
            }
         }
      }
   }
   for (i = 0; i < 3; i++) {
      printf("Minimum Cost With Respect to Node: %d\n", i);
      for (j = 0; j < 3; j++) {
         printf("%d\t", b[i][j]);
      }
   }
}

int main() {
   int b[3][3] = {0};
   b[0][1] = 10;
   b[1][2] = 15;
   b[2][0] = 12;
   floyds(b);
   return 0;
}

Minimum Cost With Respect to Node: 0
0	10	25	
Minimum Cost With Respect to Node: 1
27	0	15	
Minimum Cost With Respect to Node: 2
12	22	0	

#include <iostream>
using namespace std;
void floyds(int b[][3]){
   int i, j, k;
   for (k = 0; k < 3; k++) {
      for (i = 0; i < 3; i++) {
         for (j = 0; j < 3; j++) {
            if ((b[i][k] * b[k][j] != 0) && (i != j)) {
               if ((b[i][k] + b[k][j] < b[i][j]) || (b[i][j] == 0)) {
                  b[i][j] = b[i][k] + b[k][j];
               }
            }
         }
      }
   }
   for (i = 0; i < 3; i++) {
      cout<<"Minimum Cost With Respect to Node:"<<i<<endl;
      for (j = 0; j < 3; j++) {
         cout<<b[i][j]<<"\t";
      }
   }
}
int main(){
   int b[3][3];
   for (int i = 0; i < 3; i++) {
      for (int j = 0; j < 3; j++) {
         b[i][j] = 0;
      }
   }
   b[0][1] = 10;
   b[1][2] = 15;
   b[2][0] = 12;
   floyds(b);
   return 0;
}

Minimum Cost With Respect to Node:0
0  10  25	
Minimum Cost With Respect to Node:1
27  0  15	
Minimum Cost With Respect to Node:2
12  22  0

import java.util.Arrays;
public class Main {
   public static void floyds(int[][] b) {
      int i, j, k;
      for (k = 0; k < 3; k++) {
         for (i = 0; i < 3; i++) {
            for (j = 0; j < 3; j++) {
               if ((b[i][k] * b[k][j] != 0) && (i != j)) {
                  if ((b[i][k] + b[k][j] < b[i][j]) || (b[i][j] == 0)) {
                     b[i][j] = b[i][k] + b[k][j];
                  }
               }
            }
         }
      }
      for (i = 0; i < 3; i++) {
         System.out.println("Minimum Cost With Respect to Node:" + i);
         for (j = 0; j < 3; j++) {
            System.out.print(b[i][j] + "\t");
         }
      }
   }
   public static void main(String[] args) {
      int[][] b = new int[3][3];
      for (int i = 0; i < 3; i++) {
         Arrays.fill(b[i], 0);
      }
      b[0][1] = 10;
      b[1][2] = 15;
      b[2][0] = 12;
      floyds(b);
   }
}

Minimum Cost With Respect to Node:0
0  10  25	
Minimum Cost With Respect to Node:1
27  0  15	
Minimum Cost With Respect to Node:2
12  22  0		

import numpy as np
def floyds(b):
    for k in range(3):
        for i in range(3):
            for j in range(3):
                if (b[i][k] * b[k][j] != 0) and (i != j):
                    if (b[i][k] + b[k][j] < b[i][j]) or (b[i][j] == 0):
                        b[i][j] = b[i][k] + b[k][j]
    for i in range(3):
        print("Minimum Cost With Respect to Node:", i)
        for j in range(3):
            print(b[i][j], end="\t")
b = np.zeros((3, 3), dtype=int)
b[0][1] = 10
b[1][2] = 15
b[2][0] = 12
#calling the method
floyds(b)

Minimum Cost With Respect to Node: 0
0	10	25	
Minimum Cost With Respect to Node: 1
27	0	15	
Minimum Cost With Respect to Node: 2
12	22	0