队列数据结构

上一页
下一页

什么是队列？

队列是一种线性数据结构，其中元素按照 FIFO（先进先出）原则存储，即第一个插入的元素将是第一个被访问的元素。队列是一种抽象数据类型（ADT），类似于栈，使队列与栈不同的特点是队列的两端都是开放的。数据通过一端插入队列，并通过另一端从队列中删除。队列在大多数编程语言中被频繁使用。

car

队列的一个现实世界例子可以是一条单车道单行道，其中先进入的车辆先退出。在售票窗口和公交车站的队列也可以看到更多现实世界的例子。

队列的表示

与栈 ADT 类似，队列 ADT 也可以使用数组、链表或指针来实现。在本教程中，我们以一个小例子为例，使用一维数组实现队列。

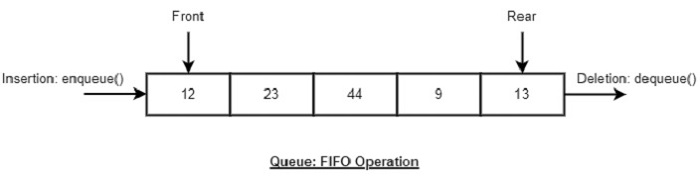
Representation of queues

队列的基本操作

队列操作还包括队列的初始化、使用以及从内存中永久删除数据。

队列 ADT 中最基本的操作包括：enqueue()、dequeue()、peek()、isFull()、isEmpty()。这些都是内置操作，用于执行数据操作和检查队列的状态。

队列使用两个指针 - front 和 rear。front 指针从前端访问数据（帮助入队），而 rear 指针从后端访问数据（帮助出队）。

队列插入操作：Enqueue()

enqueue() 是一种数据操作，用于将元素插入栈中。以下算法以更简单的方式描述了 enqueue() 操作。

算法

1. START
2. Check if the queue is full.
3. If the queue is full, produce overflow error and exit.
4. If the queue is not full, increment rear pointer to point 
   the next empty space.
5. Add data element to the queue location, where the rear 
   is pointing.
6. return success.
7. END

示例

以下是此操作在各种编程语言中的实现 -

C C++ Java Python
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
bool isEmpty(){
   return itemCount == 0;
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      printf("%d ",n);
   }
}

输出

Queue: 3 5 9 1 12 15

#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
bool isEmpty(){
   return itemCount == 0;
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      printf("%d ",n);
   }
}

输出

Queue: 3 5 9 1 12 15

import java.util.*;
public class Demo{
static final int MAX = 6;
static int intArray[] = new int[MAX];
static int front = 0;
static int rear = -1;
static int itemCount = 0;
public static boolean isFull(){
   return itemCount == MAX;
}
public static boolean isEmpty(){
   return itemCount == 0;
}
public static int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
public static void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
public static void main(String[] args){
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   System.out.print("Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      System.out.print(n + " ");
   }
  }
}

输出

Queue: 3 5 9 1 12 15 

MAX = 6;
intArray = [0] * MAX
front = 0;
rear = -1;
itemCount = 0;
def isFull():
    return itemCount == MAX
def isEmpty():
    return itemCount == 0
def removeData():
    data = intArray[front+1]
    if(front == MAX):
        front = 0
    itemCount-1
    return data
def insert(data):
    global rear, itemCount
    if(not isFull()):
        if(rear == MAX-1):
            rear = -1
        rear = rear + 1
        intArray[rear] = data
        itemCount+1
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
insert(15);
print("Queue: ")
for i in range(MAX):
    print(intArray[i], end = " ")
while(not isEmpty()):
    n = removeData()
    print(n, end = " ")

输出

Queue: 
3 5 9 1 12 15

队列删除操作：dequeue()

dequeue() 是一种数据操作，用于从栈中删除元素。以下算法以更简单的方式描述了 dequeue() 操作。

算法

1. START
2. Check if the queue is empty.
3. If the queue is empty, produce underflow error and exit.
4. If the queue is not empty, access the data where front 
   is pointing.
5. Increment front pointer to point to the next available 
   data element.
6. Return success.
7. END

示例

以下是此操作在各种编程语言中的实现 -

C C++ Java Python
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
bool isEmpty(){
   return itemCount == 0;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
int main(){
   int i;
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);

   // remove one item
   int num = removeData();
   printf("\nElement removed: %d\n",num);
   printf("Updated Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      printf("%d ",n);
   }
}

输出

Queue: 3 5 9 1 12 15 
Element removed: 3
Updated Queue: 5 9 1 12 15 

#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
bool isEmpty(){
   return itemCount == 0;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
int main(){
   int i;
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   
   // remove one item
   int num = removeData();
   printf("\nElement removed: %d\n",num);
   printf("Updated Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      printf("%d ",n);
   }
}

输出

Queue: 3 5 9 1 12 15 
Element removed: 3
Updated Queue: 5 9 1 12 15 

public class Demo{
static final int MAX = 6;
static int intArray[] = new int[MAX];
static int front = 0;
static int rear = -1;
static int itemCount = 0;
public static boolean isFull(){
   return itemCount == MAX;
}
public static boolean isEmpty(){
   return itemCount == 0;
}
public static void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
public static int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
public static void main(String[] args){
   int i;
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   System.out.print("Queue: ");
   for(i = 0; i < MAX; i++)
      System.out.print(intArray[i] + " ");
   
   // remove one item
   int num = removeData();
   System.out.print("\nElement removed: " + num);
   System.out.print("\nUpdated Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      System.out.print(n + " ");
   }
  }
}

输出

Queue: 3 5 9 1 12 15 
Element removed: 3
Updated Queue: 5 9 1 12 15 

MAX = 6
intArray = [0] * MAX
front = 0
rear = -1
itemCount = 0
def isFull():
    return itemCount == MAX
def isEmpty():
    return itemCount == 0
def insert(data):
    global rear, itemCount
    if not isFull():
        if rear == MAX-1:
            rear = -1
        rear += 1
        intArray[rear] = data
        itemCount += 1
def removeData():
    global front, itemCount
    data = intArray[front]
    if front == MAX-1:
        front = 0
    else:
        front += 1
    itemCount -= 1
    return data
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
insert(15);
print("Queue: ")
for i in range(MAX):
    print(intArray[i], end = " ")
num = removeData()
print("\nElement removed: ", num)
print("Updated Queue: ")
while(not isEmpty()):
    n = removeData()
    print(n, end = " ")

输出

Queue: 
3 5 9 1 12 15 
Element removed:  3
Updated Queue: 
5 9 1 12 15

队列 - peek() 操作

peek() 操作用于检索队列中最前面的元素，而无需删除它。此操作用于借助指针检查队列的状态。

算法

1. START
2. Return the element at the front of the queue
3. END

示例

以下是此操作在各种编程语言中的实现 -

C C++ Java Python
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
   return intArray[front];
}
bool isFull(){
   return itemCount == MAX;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   int i;
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\nElement at front: %d\n",peek());
}

输出

Queue: 3 5 9 1 12 15 
Element at front: 3

#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
   return intArray[front];
}
bool isFull(){
   return itemCount == MAX;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   int i;
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\nElement at front: %d\n",peek());
}

输出

Queue: 3 5 9 1 12 15 
Element at front: 3

public class Demo{
final static int MAX = 6;
static int intArray[] = new int[MAX];
static int front = 0;
static int rear = -1;
static int itemCount = 0;
public static int peek(){
   return intArray[front];
}
public static boolean isFull(){
   return itemCount == MAX;
}
public static void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
public static void main(String[] args){
   int i;
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   System.out.print("Queue: ");
   for(i = 0; i < MAX; i++)
      System.out.print(intArray[i] + " ");
   System.out.print("\nElement at front: " + peek());
  }
}

输出

Queue: 3 5 9 1 12 15 
Element at front: 3

MAX = 6
intArray = [0] * MAX
front = 0
rear = -1
itemCount = 0
def peek():
    return intArray[front]
def isFull():
    return itemCount == MAX
def insert(data):
    global rear, itemCount
    if(not isFull()):
        if(rear == MAX-1):
            rear = -1
        rear  = rear + 1
        intArray[rear] = data
        itemCount+1
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
insert(15);
print("Queue: ")
for i in range(MAX):
    print(intArray[i], end = " ")
print("\nElement at front: ", peek())

输出

Queue: 
3 5 9 1 12 15 
Element at front:  3

队列 - isFull() 操作

isFull() 操作验证栈是否已满。

算法

1. START
2. If the count of queue elements equals the queue size,
   return true
3. Otherwise, return false
4. END

示例

以下是此操作在各种编程语言中的实现 -

C C++ Java Python
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   int i;
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\n");
   if(isFull()) {
      printf("Queue is full!\n");
   }
}

输出

Queue: 3 5 9 1 12 15 
Queue is full!

#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   int i;
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\n");
   if(isFull()) {
      printf("Queue is full!\n");
   }
}

输出

Queue: 3 5 9 1 12 15 
Queue is full!

import java.io.*;
public class QueueExample {
   static private int intArray[];
   private int front;
   private int rear;
   private int itemCount;
   static private int MAX;
   QueueExample(int size) {
      intArray = new int[size];
      front = 0;
      rear = -1;
      MAX = size;
      itemCount = 0;
   }
   public boolean isFull() {
      return itemCount == MAX;
   }
   public void insert(int key) {
      if(!isFull()) {
         if(rear == MAX-1) {
            rear = -1;
         }
         intArray[++rear] = key;
         itemCount++;
      }
   }
   public static void main (String[] args) {
      QueueExample q = new QueueExample(5);
      q.insert(1); // inserting 1 in the stack
      q.insert(2);
      q.insert(3);
      q.insert(4);
      q.insert(5);
      System.out.print("Queue: ");
      for(int i = 0; i<MAX; i++){
          System.out.print(intArray[i] + " ");
      }
      if(q.isFull()){
	  System.out.print("\nQueue is full!");
   }
  }
}

输出

Queue: 1 2 3 4 5 
Queue is full!

#python code for isFull in Queue
MAX = 6
intArray = [None] * MAX
front = 0
rear = -1
itemCount = 0

def isFull():
    return itemCount == MAX

def insert(data):
    global rear, itemCount
    if not isFull():
        if rear == MAX-1:
            rear = -1
        rear += 1
        intArray[rear] = data
        itemCount += 1
#inserting 5 items into the Queue
insert(3)
insert(5)
insert(9)
insert(1)
insert(12)
insert(15)
print("Queue: ", end="")
for i in range(MAX):
    print(intArray[i], end=" ")
print()
if isFull():
    print("Queue is full!")

输出

Queue: 3 5 9 1 12 15 
Queue is full!

队列 - isEmpty() 操作

isEmpty() 操作验证栈是否为空。此操作用于借助 top 指针检查栈的状态。

算法

1. START
2. If the count of queue elements equals zero, return true
3. Otherwise, return false
4. END

示例

以下是此操作在各种编程语言中的实现 -

C C++ Java Python
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isEmpty(){
   return itemCount == 0;
}
int main(){
   int i;
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\n");
   if(isEmpty()) {
      printf("Queue is Empty!\n");
   }
}

输出

Queue: 0 0 0 0 0 0 
Queue is Empty!

#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isEmpty(){
   return itemCount == 0;
}
int main(){
   int i;
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\n");
   if(isEmpty()) {
      printf("Queue is Empty!\n");
   }
}

输出

Queue: 0 0 0 0 0 0 
Queue is Empty!

public class Demo{
final static int MAX = 6;
static int intArray[] = new int[MAX];
static int front = 0;
static int rear = -1;
static int itemCount = 0;
public static boolean isEmpty(){
   return itemCount == 0;
}
public static void main(String[] args){
   int i;
   System.out.print("Queue: ");
   for(i = 0; i < MAX; i++)
      System.out.print(intArray[i] + " ");
   if(isEmpty()) {
      System.out.print("\nQueue is Empty!");
   }
 }
}

输出

Queue: 0 0 0 0 0 0 
Queue is Empty!

#python code for isFull in Queue
MAX = 6
intArray = [None] * MAX
front = 0
rear = -1
itemCount = 0

def isEmpty():
    return itemCount == 0

print("Queue: ", end="")
for i in range(MAX):
    print(intArray[i], end=" ")
print()
if isEmpty():
    print("Queue is empty!")

输出

Queue: None None None None None None 
Queue is empty!

队列完整实现

以下是队列在各种编程语言中的完整实现 -

C C++ Java Python
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
   return intArray[front];
}
bool isEmpty(){
   return itemCount == 0;
}
bool isFull(){
   return itemCount == MAX;
}
int size(){
   return itemCount;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
int main(){
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue size: %d", size());
   printf("\nQueue: ");
   for(int i = 0; i < MAX; i++){
       printf("%d ", intArray[i]);
   }
   if(isFull()) {
      printf("\nQueue is full!");
   }

   // remove one item
   int num = removeData();
   printf("\nElement removed: %d", num);
   printf("\nSize of Queue after deletion: %d", size());
   printf("\nElement at front: %d", peek());
}

输出

Queue size: 6
Queue: 3 5 9 1 12 15 
Queue is full!
Element removed: 3
Size of Queue after deletion: 5
Element at front: 5

#include <iostream>
using namespace std;
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
   return intArray[front];
}
bool isEmpty(){
   return itemCount == 0;
}
bool isFull(){
   return itemCount == MAX;
}
int size(){
   return itemCount;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
int main(){
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   cout<<"Queue size: "<<size();
   cout<<"\nQueue: ";
   for(int i = 0; i < MAX; i++){
       cout<<intArray[i]<<" ";
   }
   if(isFull()) {
      cout<<"\nQueue is full!";
   }

   // remove one item
   int num = removeData();
   cout<<"\nElement removed: "<<num;
   cout<<"\nQueue size after deletion: "<<size();
   cout<<"\nElement at front: " <<peek();
}

输出

Queue size: 6
Queue: 3 5 9 1 12 15 
Queue is full!
Element removed: 3
Queue size after deletion: 5
Element at front: 5

public class Demo{
final static int MAX = 6;
static int intArray[] = new int[MAX];
static int front = 0;
static int rear = -1;
static int itemCount = 0;
public static int peek(){
   return intArray[front];
}
public static boolean isEmpty(){
   return itemCount == 0;
}
public static boolean isFull(){
   return itemCount == MAX;
}
public static int size(){
   return itemCount;
}
public static void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
public static int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
public static void main(String[] args){
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   System.out.print("Queue size: " + size());
   System.out.print("\nQueue: ");
   for(int i = 0; i < MAX; i++){
       System.out.print(intArray[i] + " ");
   }
   if(isFull()) {
      System.out.print("\nQueue is full!");
   }

   // remove one item
   int num = removeData();
   System.out.print("\nElement removed: " + num);
   System.out.print("\nQueue size after deletion: " + size());
   System.out.print("\nElement at front: " + peek());
 }
}

输出

Queue size: 6
Queue: 3 5 9 1 12 15 
Queue is full!
Element removed: 3
Queue size after deletion: 5
Element at front: 5

MAX = 6
intArray = [0] * MAX
front = 0
rear = -1
itemCount = 0
def peek():
    return intArray[front]

def isEmpty():
    return itemCount == 0

def isFull():
    return itemCount == MAX

def size():
    return itemCount

def insert(data):
    global rear, itemCount
    if not isFull():
        if rear == MAX-1:
            rear = -1
        rear += 1
        intArray[rear] = data
        itemCount += 1

def removeData():
    global front, itemCount
    data = intArray[front]
    if front == MAX-1:
        front = 0
    else:
        front += 1
    itemCount -= 1
    return data

def main():
    insert(3)
    insert(5)
    insert(9)
    insert(1)
    insert(12)
    insert(15)
    print("Queue size: ", size())
    print("Queue: ")
    for i in range(MAX):
        print(intArray[i], end = " ")
    if isFull():
        print("\nQueue is full!")
    num = removeData()
    print("Element removed: ", num)
    print("Queue size after deletion: ", size())
    print("Element at front: ", peek())

main()

输出

Queue size:  6
Queue: 
3 5 9 1 12 15 
Queue is full!
Element removed:  3
Queue size after deletion:  5
Element at front:  5

C语言中的队列实现

点击查看使用C语言编写的队列程序的实现

打印页面
上一页
下一页
广告