汉诺塔问题（使用递归）

Table of content

汉诺塔
规则
算法
示例

汉诺塔

汉诺塔是一个数学游戏，由三个塔（桩）和多个环组成，如下图所示：

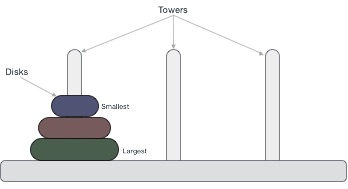
这些环大小不同，按升序排列堆叠，即较小的环放在较大的环上面。该游戏的其他变体中，圆盘的数量会增加，但塔的数量保持不变。

规则

任务是将所有圆盘移动到另一个塔，而不违反排列顺序。汉诺塔游戏需要遵循以下规则：

在任何给定时间，只能在塔之间移动一个圆盘。
只能移动“顶部”的圆盘。
较大的圆盘不能放在较小的圆盘上面。

以下是使用三个圆盘解决汉诺塔游戏的动画演示。

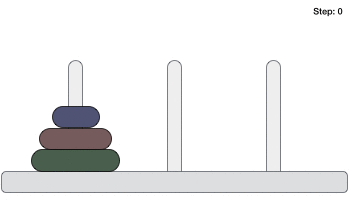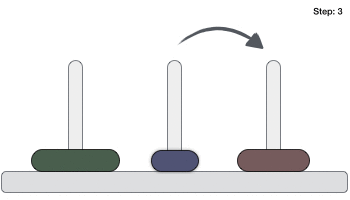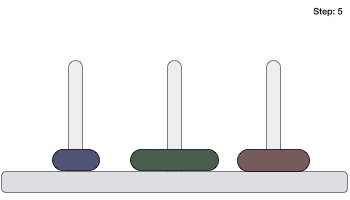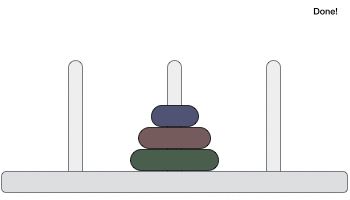
包含 n 个圆盘的汉诺塔游戏最少需要 2ⁿ−1 步才能解决。此演示显示，包含 3 个圆盘的游戏需要 2³ - 1 = 7 步。

算法

要编写汉诺塔游戏的算法，首先我们需要学习如何使用较少的圆盘（例如 1 或 2）来解决此问题。我们将三个塔分别命名为源、目标和辅助（仅用于帮助移动圆盘）。如果只有一个圆盘，则可以轻松地将其从源塔移动到目标塔。

如果有 2 个圆盘：

首先，我们将较小的（顶部）圆盘移动到辅助塔。
然后，我们将较大的（底部）圆盘移动到目标塔。
最后，我们将较小的圆盘从辅助塔移动到目标塔。

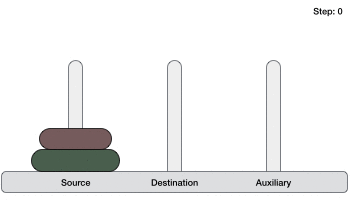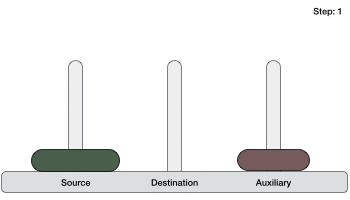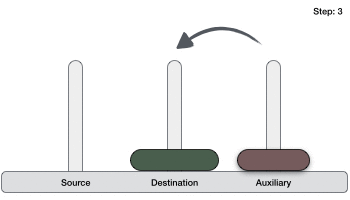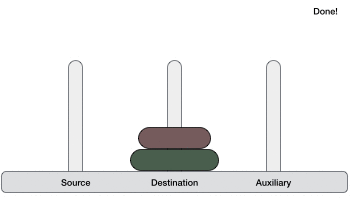
因此，现在我们可以设计一个用于解决包含两个以上圆盘的汉诺塔游戏的算法。我们将圆盘堆栈分成两部分。最大的圆盘（第 n 个圆盘）在一部分，所有其他（n-1）个圆盘在另一部分。

我们的最终目标是从源塔将第 n 个圆盘移动到目标塔，然后将所有其他（n-1）个圆盘放在它上面。我们可以想象以递归的方式对所有给定的圆盘集应用相同的操作。

需要遵循的步骤：

Step 1 − Move n-1 disks from source to aux
Step 2 − Move n^th disk from source to dest
Step 3 − Move n-1 disks from aux to dest

汉诺塔游戏的递归算法可以如下所示：

START
Procedure Hanoi(disk, source, dest, aux)

   IF disk == 1, THEN
      move disk from source to dest             
   ELSE
      Hanoi(disk - 1, source, aux, dest)     // Step 1
      move disk from source to dest          // Step 2
      Hanoi(disk - 1, aux, dest, source)     // Step 3
   END IF
   
END Procedure
STOP

示例

以下是此方法在各种编程语言中的实现：

C C++ Java Python

#include <stdio.h>
void hanoi(int n, char from, char to, char via) {
   if(n == 1){
      printf("Move disk 1 from %c to %c\n", from, to);
   }
   else{
      hanoi(n-1, from, via, to);
      printf("Move disk %d from %c to %c\n", n, from, to);
      hanoi(n-1, via, to, from);
   }
}
int main() {
   int n = 3;
   char from = 'A';
   char to = 'B';
   char via = 'C';
   //calling hanoi() method
   hanoi(n, from, via, to);
}

#include <iostream>
using namespace std;
void hanoi(int n, char from, char to, char via) {
   if(n == 1){
      cout<<"Move disk 1 from "<<from<<" to "<<to<<endl;
   }
   else{
      hanoi(n-1, from, via, to);
      cout<<"Move disk "<<n<<" from "<<from<<" to "<<to<<endl;
      hanoi(n-1, via, to, from);
   }
}
int main() {
   int n = 3;
   char from = 'A';
   char to = 'B';
   char via = 'C';
   //calling hanoi() method
   hanoi(n, from , via, to);
}

import java.util.*;
public class Demo {
   public static void hanoi(int n, String from, String to, String via) {
      if(n == 1){
         System.out.println("Move disk 1 from " + from + " to " + to);
      }
      else{
         hanoi(n-1, from, via, to);
         System.out.println("Move disk " + n + " from " + from + " to " + to);
         hanoi(n-1, via, to, from);
      }
   }
   public static void main(String[] args) {
      int n = 3;
      String from = "A";
      String to = "B";
      String via = "C";
      //calling hanoi() metod
      hanoi(n, from, via, to);
   }
}

def hanoi(n, f, to, via):
    if n == 1:
        print("Move disk 1 from",f,"to",to);
    else:
        hanoi(n-1, f, via, to)
        print("Move disk",n,"from",f,"to",to);
        hanoi(n-1, via, to, f)
n = 3
f = 'A'
to = 'B'
via = 'C'
hanoi(n, f, via, to)

输出

Move disk 1 from A to C
Move disk 2 from A to B
Move disk 1 from C to B
Move disk 3 from A to C
Move disk 1 from B to A
Move disk 2 from B to C
Move disk 1 from A to C

打印页面