归并排序算法

归并排序是一种基于分治技术的排序技术。其最坏时间复杂度为Ο(n log n)，是使用最广泛和最受青睐的算法之一。

归并排序首先将数组分成相等的两半，然后以排序的方式将它们合并。

归并排序是如何工作的？

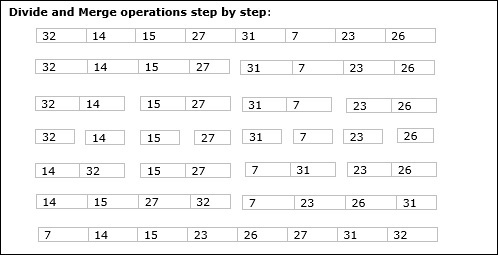
为了理解归并排序，我们以一个未排序的数组为例：

我们知道归并排序首先迭代地将整个数组分成相等的两半，直到达到原子值。这里我们看到一个包含8个元素的数组被分成两个大小为4的数组。

这不会改变元素在原始数组中的出现顺序。现在我们将这两个数组分成两半。

我们进一步划分这些数组，并获得无法再划分的原子值。

现在，我们将它们以与分解时完全相同的方式合并。请注意给这些列表提供的颜色代码。

我们首先比较每个列表的元素，然后以排序的方式将它们合并到另一个列表中。我们看到14和33处于排序位置。我们比较27和10，在目标列表的2个值中，我们首先放置10，然后是27。我们改变19和35的顺序，而42和44按顺序放置。

在合并阶段的下一轮迭代中，我们比较两个数据值的列表，并将它们合并到一个已找到数据值的列表中，并将所有数据按排序顺序放置。

最终合并后，列表变为排序状态，并被认为是最终解决方案。

归并排序算法

归并排序不断将列表分成相等的两半，直到无法再划分。根据定义，如果列表中只有一个元素，则认为它是已排序的。然后，归并排序合并较小的已排序列表，同时保持新列表也已排序。

Step 1: If it is only one element in the list, consider it already 
sorted, so return.
Step 2: Divide the list recursively into two halves until it can no  
more be divided.
Step 3: Merge the smaller lists into new list in sorted order.

伪代码

现在我们将看到归并排序函数的伪代码。正如我们的算法指出的那样，有两个主要函数——划分和合并。

归并排序使用递归，我们将以相同的方式查看我们的实现。

procedure mergesort( var a as array )
   if ( n == 1 ) return a
      var l1 as array = a[0] ... a[n/2]
      var l2 as array = a[n/2+1] ... a[n]
      l1 = mergesort( l1 )
      l2 = mergesort( l2 )
      return merge( l1, l2 )
end procedure
procedure merge( var a as array, var b as array )
   var c as array
   while ( a and b have elements )
      if ( a[0] > b[0] )
         add b[0] to the end of c
         remove b[0] from b
      else
         add a[0] to the end of c
         remove a[0] from a
      end if
   end while
   while ( a has elements )
      add a[0] to the end of c
      remove a[0] from a
   end while
   while ( b has elements )
      add b[0] to the end of c
      remove b[0] from b
   end while
   return c
end procedure

示例

在下面的示例中，我们逐步展示了归并排序算法。首先，每次迭代数组都被分成两个子数组，直到子数组只包含一个元素。当这些子数组无法进一步划分时，执行合并操作。

分析

让我们考虑一下归并排序的运行时间为T(n)。因此，

$$\mathrm{T\left ( n \right )=\left\{\begin{matrix} c & if\, n\leq 1 \\ 2\, xT\left ( \frac{n}{2} \right )+dxn &otherwise \\ \end{matrix}\right.}\:其中\: c\: 和\: d\: 是\: 常数$$

因此，使用此递归关系，

$$T\left ( n \right )=2^{i}\, T\left ( n/2^{i} \right )+i\cdot d\cdot n$$

$$由于,\:\: i=log\: n,\: T\left ( n \right )=2^{log\, n}T\left ( n/2^{log\, n} \right )+log\, n\cdot d\cdot n$$

$$=c\cdot n+d\cdot n\cdot log\: n$$

$$因此,\: \: T\left ( n \right ) = O(n\: log\: n ).$$

示例

以下是上述方法在各种编程语言中的实现：

#include <stdio.h>
#define max 10
int a[11] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44, 0 };
int b[10];
void merging(int low, int mid, int high){
   int l1, l2, i;
   for(l1 = low, l2 = mid + 1, i = low; l1 <= mid && l2 <= high; i++) {
      if(a[l1] <= a[l2])
         b[i] = a[l1++];
      else
         b[i] = a[l2++];
   }
   while(l1 <= mid)
      b[i++] = a[l1++];
   while(l2 <= high)
      b[i++] = a[l2++];
   for(i = low; i <= high; i++)
      a[i] = b[i];
}
void sort(int low, int high){
   int mid;
   if(low < high) {
      mid = (low + high) / 2;
      sort(low, mid);
      sort(mid+1, high);
      merging(low, mid, high);
   } else {
      return;
   }
}
int main(){
   int i;
   printf("Array before sorting\n");
   for(i = 0; i <= max; i++)
      printf("%d ", a[i]);
   sort(0, max);
   printf("\nArray after sorting\n");
   for(i = 0; i <= max; i++)
      printf("%d ", a[i]);
}

Array before sorting
10 14 19 26 27 31 33 35 42 44 0 
Array after sorting
0 10 14 19 26 27 31 33 35 42 44 

#include <iostream>
using namespace std;
#define max 10
int a[11] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44, 0 };
int b[10];
void merging(int low, int mid, int high){
   int l1, l2, i;
   for(l1 = low, l2 = mid + 1, i = low; l1 <= mid && l2 <= high; i++) {
      if(a[l1] <= a[l2])
         b[i] = a[l1++];
      else
         b[i] = a[l2++];
   }
   while(l1 <= mid)
      b[i++] = a[l1++];
   while(l2 <= high)
      b[i++] = a[l2++];
   for(i = low; i <= high; i++)
      a[i] = b[i];
}
void sort(int low, int high){
   int mid;
   if(low < high) {
      mid = (low + high) / 2;
      sort(low, mid);
      sort(mid+1, high);
      merging(low, mid, high);
   } else {
      return;
   }
}
int main(){
   int i;
   cout << "Array before sorting\n";
   for(i = 0; i <= max; i++)
      cout<<a[i]<<" ";
   sort(0, max);
   cout<< "\nArray after sorting\n";
   for(i = 0; i <= max; i++)
      cout<<a[i]<<" ";
}

Array before sorting
10 14 19 26 27 31 33 35 42 44 0 
Array after sorting
0 10 14 19 26 27 31 33 35 42 44 

public class Merge_Sort {
   static int a[] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44, 0 };
   static int b[] = new int[a.length];
   static void merging(int low, int mid, int high) {
      int l1, l2, i;
      for(l1 = low, l2 = mid + 1, i = low; l1 <= mid && l2 <= high; i++) {
         if(a[l1] <= a[l2])
            b[i] = a[l1++];
         else
            b[i] = a[l2++];
      }
      while(l1 <= mid)
         b[i++] = a[l1++];
      while(l2 <= high)
         b[i++] = a[l2++];
      for(i = low; i <= high; i++)
         a[i] = b[i];
   }
   static void sort(int low, int high) {
      int mid;
      if(low < high) {
         mid = (low + high) / 2;
         sort(low, mid);
         sort(mid+1, high);
         merging(low, mid, high);
      } else {
         return;
      }
   }
   public static void main(String args[]) {
      int i;
      int n = a.length;
      System.out.println("Array before sorting");
      for(i = 0; i < n; i++)
         System.out.print(a[i] + " ");
      sort(0, n-1);
      System.out.println("\nArray after sorting");
      for(i = 0; i < n; i++)
         System.out.print(a[i]+" ");
   }
}

Array before sorting
10 14 19 26 27 31 33 35 42 44 0 
Array after sorting
0 10 14 19 26 27 31 33 35 42 44

def merge_sort(a, n):
   if n > 1:
      m = n // 2
      #divide the list in two sub lists
      l1 = a[:m]
      n1 = len(l1)
      l2 = a[m:]
      n2 = len(l2)
      #recursively calling the function for sub lists
      merge_sort(l1, n1)
      merge_sort(l2, n2)
      i = j = k = 0
      while i < n1 and j < n2:
         if l1[i] <= l2[j]:
            a[k] = l1[i]
            i = i + 1
         else:
            a[k] = l2[j]
            j = j + 1
         k = k + 1
      while i < n1:
         a[k] = l1[i]
         i = i + 1
         k = k + 1    
      while j < n2:
         a[k]=l2[j]
         j = j + 1
         k = k + 1

a = [10, 14, 19, 26, 27, 31, 33, 35, 42, 44, 0]
n = len(a)
print("Array before Sorting")
print(a)
merge_sort(a, n)
print("Array after Sorting")
print(a)

Array before Sorting
[10, 14, 19, 26, 27, 31, 33, 35, 42, 44, 0]
Array after Sorting
[0, 10, 14, 19, 26, 27, 31, 33, 35, 42, 44]