克鲁斯卡尔最小生成树算法

Table of content
上一页
下一页

克鲁斯卡尔最小生成树算法是寻找图的最小生成树的有效方法之一。最小生成树是一个子图，它以最少的边和最小成本（分配给每条边的权重之和）连接主图中的所有顶点。

该算法首先从图的森林开始——定义为仅包含主图顶点的子图——然后添加成本最低的边，直到创建最小生成树，而不会在图中形成环。

克鲁斯卡尔算法比普里姆算法更容易实现，但复杂度更高。

克鲁斯卡尔算法

克鲁斯卡尔算法的输入是图 G {V, E}，其中 V 是顶点集，E 是边集，以及源顶点 S，输出是图 G 的最小生成树。

算法

  • 将图中所有边按升序排序，并将其存储在数组edge[] 中。

  • 在平面上构造图的森林，其中包含所有顶点。

  • 从edge[]数组中选择成本最低的边，并将其添加到图的森林中。通过将访问过的顶点添加到visited[]数组中来标记已访问的顶点。

  • 重复步骤2和3，直到所有顶点都被访问，并且图中没有形成任何环。

  • 当所有顶点都被访问时，最小生成树就形成了。

  • 计算形成的输出生成树的最小成本。

示例

使用克鲁斯卡尔算法为下面给出的图构造最小生成树：

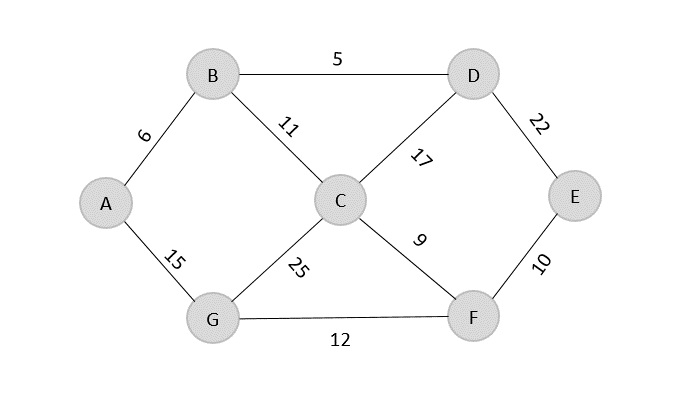
kruskals_algorithm_graph

解决方案

第一步，将给定图中的所有边按升序排序，并将值存储在数组中。

边 B→D A→B C→F F→E B→C G→F A→G C→D D→E C→G
成本 5 6 9 10 11 12 15 17 22 25

然后，在一个平面上构造给定图的森林。

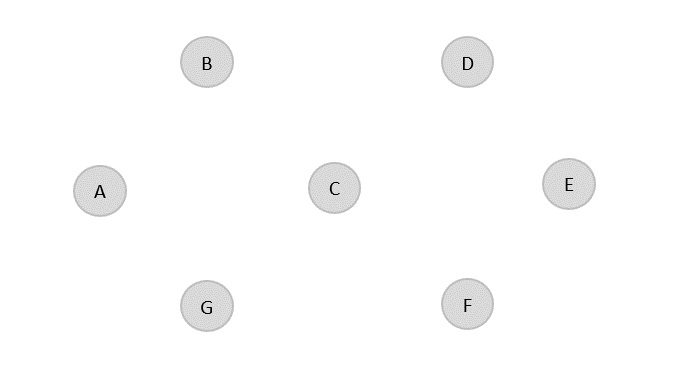
graph_on_single_plane

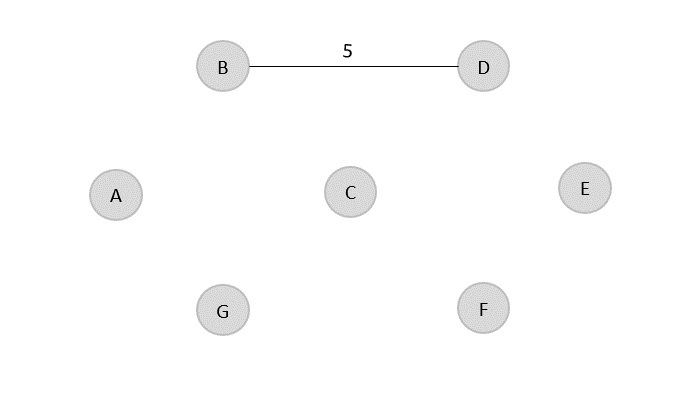
从排序的边成本列表中，选择成本最低的边，并将其添加到输出图的森林中。

B → D = 5
Minimum cost = 5
Visited array, v = {B, D}
sorted_edge_costs

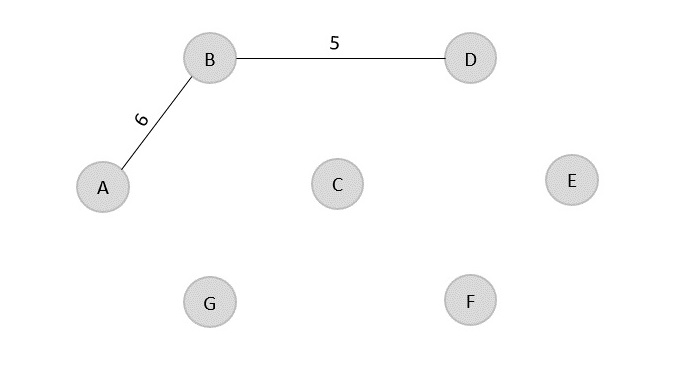
类似地，下一个成本最低的边是 B → A = 6；因此，我们将其添加到输出图中。

Minimum cost = 5 + 6 = 11
Visited array, v = {B, D, A}
graph_b_to_a

下一个成本最低的边是 C → F = 9；将其添加到输出图中。

Minimum Cost = 5 + 6 + 9 = 20
Visited array, v = {B, D, A, C, F}
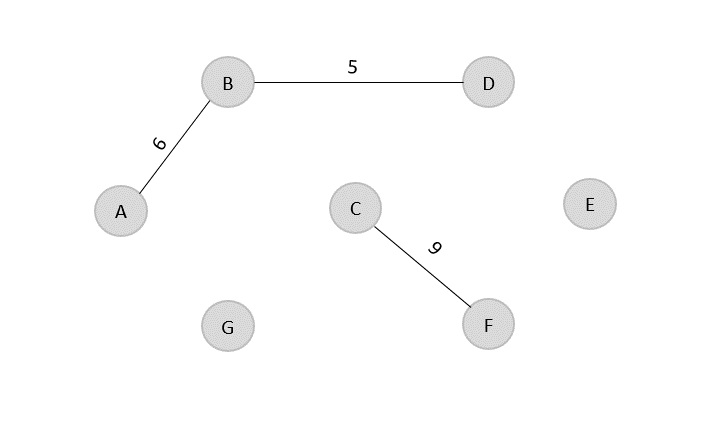
graph_c_to_f

下一个要添加到输出图的边是 F → E = 10。

Minimum Cost = 5 + 6 + 9 + 10 = 30
Visited array, v = {B, D, A, C, F, E}
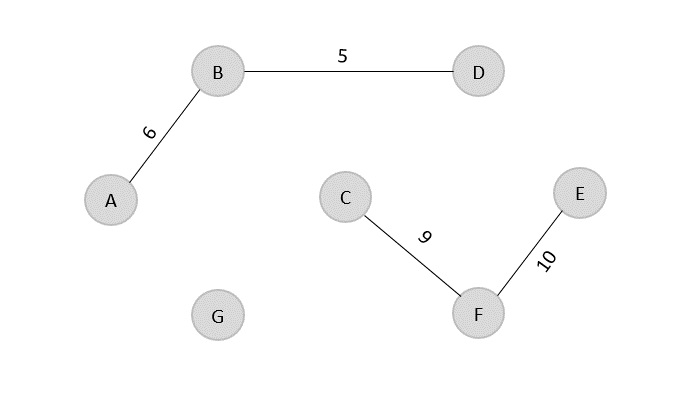
output_graph_e_to_f

来自成本最低数组的下一条边是 B → C = 11，因此我们将其添加到输出图中。

Minimum cost = 5 + 6 + 9 + 10 + 11 = 41
Visited array, v = {B, D, A, C, F, E}
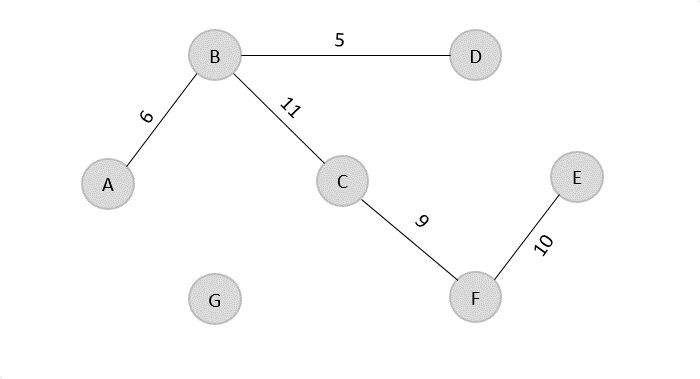
least_cost_array

要添加到输出图的来自成本最低数组的最后一条边是 F → G = 12。

Minimum cost = 5 + 6 + 9 + 10 + 11 + 12 = 53
Visited array, v = {B, D, A, C, F, E, G}
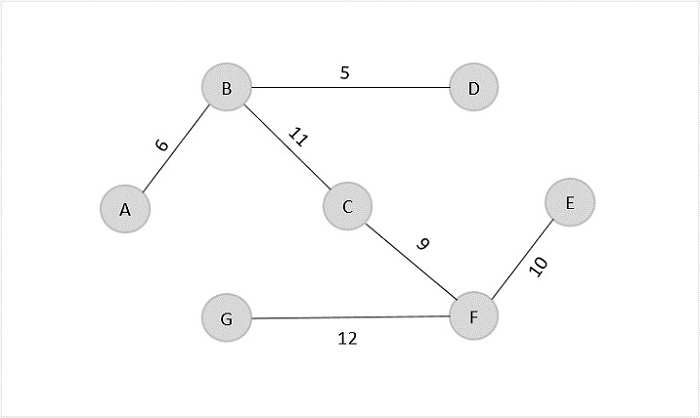
output_graph_f_to_g

获得的结果是给定图的最小生成树，成本 = 53。

示例

最终程序实现了克鲁斯卡尔最小生成树问题，该问题将成本邻接矩阵作为输入，并打印最短路径以及最小成本作为输出。

C C++ Java Python
#include <stdio.h>
#include <stdlib.h>
const int inf = 999999;
int k, a, b, u, v, n, ne = 1;
int mincost = 0;
int cost[3][3] = {{0, 10, 20},{12, 0,15},{16, 18, 0}};
int  p[9] = {0};
int applyfind(int i)
{
    while(p[i] != 0)
        i=p[i];
    return i;
}
int applyunion(int i,int j)
{
    if(i!=j) {
        p[j]=i;
        return 1;
    }
    return 0;
}
int main()
{
    n = 3;
    int i, j;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            if (cost[i][j] == 0) {
                cost[i][j] = inf;
            }
        }
    }
    printf("Minimum Cost Spanning Tree: \n");
    while(ne < n) {
        int min_val = inf;
        for(i=0; i<n; i++) {
            for(j=0; j <n; j++) {
                if(cost[i][j] < min_val) {
                    min_val = cost[i][j];
                    a = u = i;
                    b = v = j;
                }
            }
        }
        u = applyfind(u);
        v = applyfind(v);
        if(applyunion(u, v) != 0) {
            printf("%d -> %d\n", a, b);
            mincost +=min_val;
        }
        cost[a][b] = cost[b][a] = 999;
        ne++;
    }
    printf("Minimum cost = %d",mincost);
    return 0;
}

输出

Minimum Cost Spanning Tree: 
0 -> 1
1 -> 2
Minimum cost = 25

#include <iostream>
using namespace std;
const int inf = 999999;
int k, a, b, u, v, n, ne = 1;
int mincost = 0;
int cost[3][3] = {{0, 10, 20}, {12, 0, 15}, {16, 18, 0}};
int p[9] = {0};
int applyfind(int i)
{
    while (p[i] != 0) {
        i = p[i];
    }
    return i;
}
int applyunion(int i, int j)
{
    if (i != j) {
        p[j] = i;
        return 1;
    }
    return 0;
}
int main()
{
    n = 3;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            if (cost[i][j] == 0) {
                cost[i][j] = inf;
            }
        }
    }
    cout << "Minimum Cost Spanning Tree:\n";
    while (ne < n) {
        int min_val = inf;
        for (int i = 0; i < n; i++) {
            for (int j = 0;
                    j < n; j++) {
                if (cost[i][j] < min_val) {
                    min_val = cost[i][j];
                    a = u = i;
                    b = v = j;
                }
            }
        }
        u = applyfind(u);
        v = applyfind(v);
        if (applyunion(u, v) != 0) {
            cout << a << " -> " << b << "\n";
            mincost += min_val;
        }
        cost[a][b] = cost[b][a] = 999;
        ne++;
    }
    cout << "Minimum cost = " << mincost << endl;
    return 0;
}

输出

Minimum Cost Spanning Tree:
0 -> 1
1 -> 2
Minimum cost = 25

import java.util.*;
public class Main {
   static int k, a, b, u, v, n, ne = 1, min, mincost = 0;
   static int cost[][] = {{0, 10, 20},{12, 0, 15},{16, 18, 0}};
   static int p[] = new int[9];
   static int inf = 999999;
   static int applyfind(int i) {
      while(p[i] != 0)
      i=p[i];
      return i;
   }
   static int applyunion(int i,int j) {
      if(i!=j) {
         p[j]=i;
         return 1;
      }
      return 0;
   }
   public static void main(String args[]) {
      int i, j;
      n = 3;
      for(i=0; i<n; i++)
      for(j=0; j<n; j++) {
         if(cost[i][j]==0)
         cost[i][j]= inf;
      }
      System.out.println("Minimum Cost Spanning Tree: ");
      while(ne < n) {
         min = inf;
         for(i=0; i<n; i++) {
            for(j=0; j<n; j++) {
               if(cost[i][j] < min) {
                  min=cost[i][j];
                  a=u=i;
                  b=v=j;
               }
            }
         }
         u=applyfind(u);
         v=applyfind(v);
         if(applyunion(u,v) != 0) {
            System.out.println(a + " -> " + b);
            mincost += min;
         }
         cost[a][b]=cost[b][a]=999;
         ne +=1;
      }
      System.out.println("Minimum cost = " + mincost);
   }
}

输出

Minimum Cost Spanning Tree: 
0 -> 1
1 -> 2
Minimum cost = 25

inf = 999999
k, a, b, u, v, n, ne = 0, 0, 0, 0, 0, 0, 1
mincost = 0
cost = [[0, 10, 20], [12, 0, 15], [16, 18, 0]]
p = [0] * 9
def applyfind(i):
    while p[i] != 0:
        i = p[i]
    return i
def applyunion(i, j):
    if i != j:
        p[j] = i
        return 1
    return 0
n = 3
for i in range(n):
    for j in range(n):
        if cost[i][j] == 0:
            cost[i][j] = inf
print("Minimum Cost Spanning Tree:")
while ne < n:
    min_val = inf
    for i in range(n):
        for j in range(n):
            if cost[i][j] < min_val:
                min_val = cost[i][j]
                a = u = i
                b = v = j
    u = applyfind(u)
    v = applyfind(v)
    if applyunion(u, v) != 0:
        print(f"{a} -> {b}")
        mincost += min_val
    cost[a][b] = cost[b][a] = 999
    ne += 1
print(f"Minimum cost = {mincost}")

输出

Minimum Cost Spanning Tree: 
0 -> 1
1 -> 2
Minimum cost = 25
打印页面
上一页
下一页
广告