B树

Table of content

B树的基本操作
插入操作
删除操作

B树是扩展的二叉搜索树，专门用于m路搜索，因为B树的阶数为'm'。树的阶数定义为一个节点可以容纳的最大子节点数。因此，B树的高度相对小于AVL树和红黑树的高度。

它们是二叉搜索树的通用形式，因为它可以保存多个键和两个子节点。

B树的各种特性包括 -

B树中的每个节点最多可以容纳m个子节点和(m-1)个键，因为树的阶数为m。
B树中除根节点和叶子节点外的每个节点至少可以容纳m/2个子节点
根节点必须至少有两个子节点。
B树中的所有路径必须在同一级别结束，即叶子节点必须在同一级别。
B树始终保持数据排序。

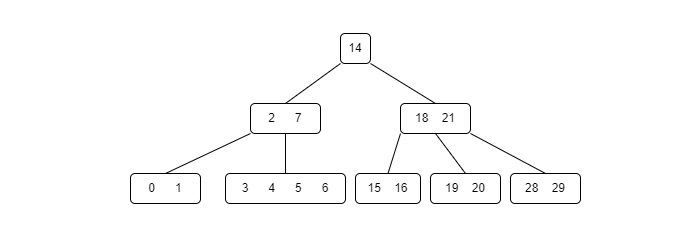
B树也广泛用于磁盘访问，由于B树的高度较低，因此可以最大程度地减少磁盘访问时间。

注意 - 磁盘访问是指对存储信息的计算机磁盘的内存访问，磁盘访问时间是指系统访问磁盘内存所需的时间。

B树的基本操作

B树支持的操作包括插入、删除和搜索，每个操作的时间复杂度为O(log n)。

插入操作

B树的插入操作类似于二叉搜索树，但元素会插入到同一个节点，直到达到最大键数。插入操作使用以下步骤进行 -

步骤1 - 计算节点可以容纳的最大 $\mathrm{\left ( m-1 \right )}$ 和最小 $\mathrm{\left ( \left \lceil \frac{m}{2}\right \rceil-1 \right )}$ 键数，其中m表示B树的阶数。

步骤2 - 使用二分搜索插入将数据插入到树中，并且一旦键达到最大数量，节点就会被分成两半，中间键成为内部节点，而左右键成为其子节点。

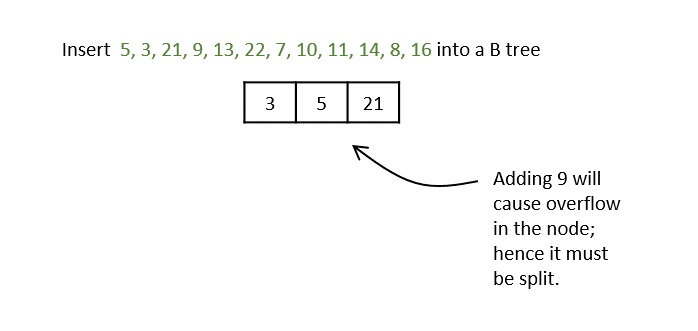
步骤3 - 所有叶子节点必须在同一级别。

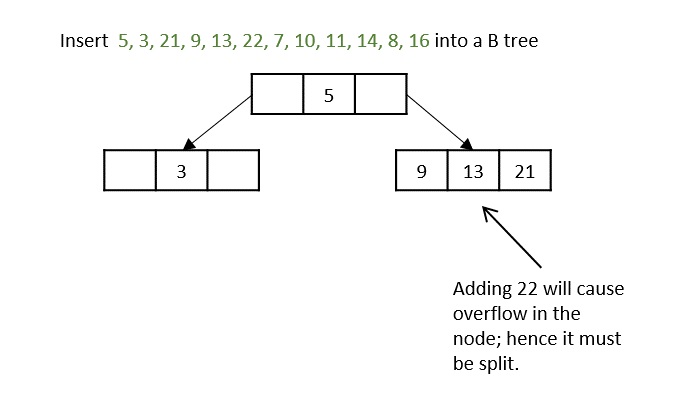
键5、3、21、9、13都根据二分搜索属性添加到节点中，但是如果我们添加键22，它将违反最大键属性。因此，节点被分成两半，中间键移到父节点，然后继续插入操作。

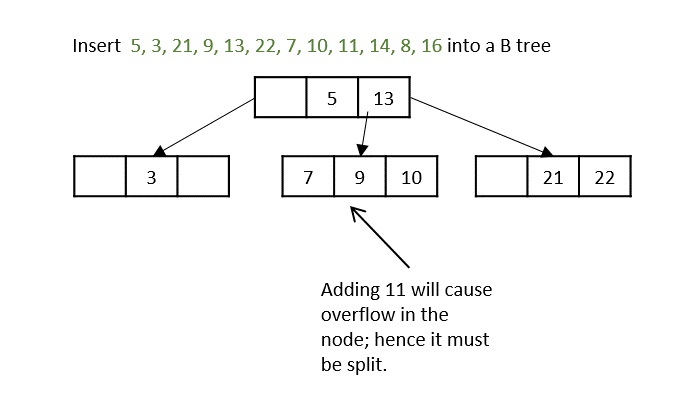
在插入11时出现另一个问题，因此节点被分割，中间键移到父节点。

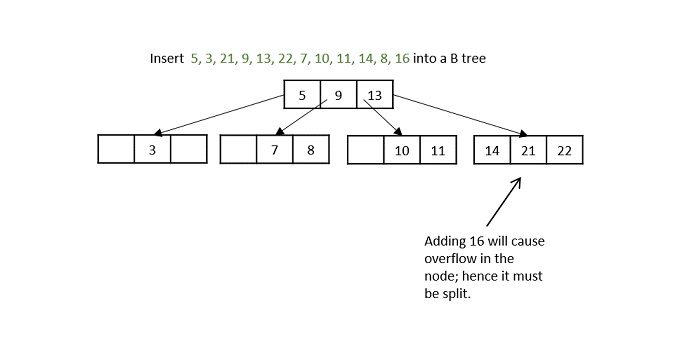
在插入16时，即使节点被分成两部分，父节点也会溢出，因为它达到了最大键数。因此，首先分割父节点，中间键成为根节点。然后，将叶子节点分成两半，并将叶子节点的中位数移到其父节点。

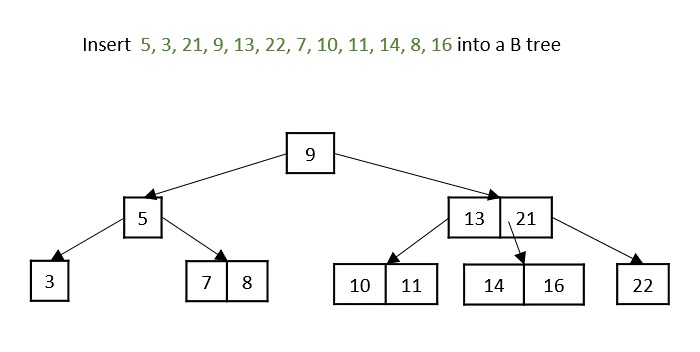
插入所有元素后，最终的B树就形成了。

示例

以下是此操作在各种编程语言中的实现 -

C C++ Java Python

// C Program for B trees 
#include <stdio.h>
#include <stdlib.h>
struct BTree {
    //node declaration
   int *d;
   struct BTree **child_ptr;
   int l;
   int n;
};
struct BTree *r = NULL;
struct BTree *np = NULL;
struct BTree *x = NULL;
//creation of node
struct BTree* init() {
   int i;
   np = (struct BTree*)malloc(sizeof(struct BTree));
   //order 6
   np->d = (int*)malloc(6 * sizeof(int));
   np->child_ptr = (struct BTree**)malloc(7 * sizeof(struct BTree*));
   np->l = 1;
   np->n = 0;
   for (i = 0; i < 7; i++) {
      np->child_ptr[i] = NULL;
   }
   return np;
}
//traverse the tree
void traverse(struct BTree *p) {
   printf("\n");
   int i;
   for (i = 0; i < p->n; i++) {
      if (p->l == 0) {
         traverse(p->child_ptr[i]);
      }
      printf(" %d", p->d[i]);
   }
   if (p->l == 0) {
      traverse(p->child_ptr[i]);
   }
   printf("\n");
}
//sort the tree
void sort(int *p, int n) {
   int i, j, t;
   for (i = 0; i < n; i++) {
      for (j = i; j <= n; j++) {
         if (p[i] > p[j]) {
            t = p[i];
            p[i] = p[j];
            p[j] = t;
         }
      }
   }
}
int split_child(struct BTree *x, int i) {
   int j, mid;
   struct BTree *np1, *np3, *y;
   np3 = init();
   //create new node
   np3->l = 1;
   if (i == -1) {
      mid = x->d[2];
      //find mid
      x->d[2] = 0;
      x->n--;
      np1 = init();
      np1->l = 0;
      x->l = 1;
      for (j = 3; j < 6; j++) {
         np3->d[j - 3] = x->d[j];
         np3->child_ptr[j - 3] = x->child_ptr[j];
         np3->n++;
         x->d[j] = 0;
         x->n--;
      }
      for (j = 0; j < 6; j++) {
         x->child_ptr[j] = NULL;
      }
      np1->d[0] = mid;
      np1->child_ptr[np1->n] = x;
      np1->child_ptr[np1->n + 1] = np3;
      np1->n++;
      r = np1;
   } else {
      y = x->child_ptr[i];
      mid = y->d[2];
      y->d[2] = 0;
      y->n--;
      for (j = 3; j < 6; j++) {
         np3->d[j - 3] = y->d[j];
         np3->n++;
         y->d[j] = 0;
         y->n--;
      }
      x->child_ptr[i + 1] = y;
      x->child_ptr[i + 1] = np3;
   }
   return mid;
}
void insert(int a) {
   int i, t;
   x = r;
   if (x == NULL) {
      r = init();
      x = r;
   } else {
      if (x->l == 1 && x->n == 6) {
         t = split_child(x, -1);
         x = r;
         for (i = 0; i < x->n; i++) {
            if (a > x->d[i] && a < x->d[i + 1]) {
               i++;
               break;
            } else if (a < x->d[0]) {
               break;
            } else {
               continue;
            }
         }
         x = x->child_ptr[i];
      } else {
         while (x->l == 0) {
            for (i = 0; i < x->n; i++) {
               if (a > x->d[i] && a < x->d[i + 1]) {
                  i++;
                  break;
               } else if (a < x->d[0]) {
                  break;
               } else {
                  continue;
               }
            }
            if (x->child_ptr[i]->n == 6) {
               t = split_child(x, i);
               x->d[x->n] = t;
               x->n++;
               continue;
            } else {
               x = x->child_ptr[i];
            }
         }
      }
   }
   x->d[x->n] = a;
   sort(x->d, x->n);
   x->n++;
}

int main() {
   int i, n, t;
   insert(10);
   insert(20);
   insert(30);
   insert(40);
   insert(50);
   printf("Insertion Done");
   printf("\nB tree:");
   traverse(r);
   return 0;
}

输出

Insertion Done
B tree:
 10 20 30 40 50

#include<iostream>
using namespace std;
struct BTree {//node declaration
   int *d;
   BTree **child_ptr;
   bool l;
   int n;
}*r = NULL, *np = NULL, *x = NULL;

BTree* init() {//creation of node
   int i;
   np = new BTree;
   np->d = new int[6];//order 6
   np->child_ptr = new BTree *[7];
   np->l = true;
   np->n = 0;
   for (i = 0; i < 7; i++) {
      np->child_ptr[i] = NULL;
   }
   return np;
}

void traverse(BTree *p) { //traverse the tree
   cout<<endl;
   int i;
   for (i = 0; i < p->n; i++) {
      if (p->l == false) {
         traverse(p->child_ptr[i]);
      }
      cout << " " << p->d[i];
   }
   if (p->l == false) {
      traverse(p->child_ptr[i]);
   }
   cout<<endl;
}

void sort(int *p, int n){ //sort the tree
   int i, j, t;
   for (i = 0; i < n; i++) {
      for (j = i; j <= n; j++) {
         if (p[i] >p[j]) {
            t = p[i];
            p[i] = p[j];
            p[j] = t;
         }
      }
   }
}

int split_child(BTree *x, int i) {
   int j, mid;
   BTree *np1, *np3, *y;
   np3 = init();//create new node
   np3->l = true;
   if (i == -1) {
      mid = x->d[2];//find mid
      x->d[2] = 0;
      x->n--;
      np1 = init();
      np1->l= false;
      x->l= true;
      for (j = 3; j < 6; j++) {
         np3->d[j - 3] = x->d[j];
         np3->child_ptr[j - 3] = x->child_ptr[j];
         np3->n++;
         x->d[j] = 0;
         x->n--;
      }
      for (j = 0; j < 6; j++) {
         x->child_ptr[j] = NULL;
      }
      np1->d[0] = mid;
      np1->child_ptr[np1->n] = x;
      np1->child_ptr[np1->n + 1] = np3;
      np1->n++;
      r = np1;
   } else {
      y = x->child_ptr[i];
      mid = y->d[2];
      y->d[2] = 0;
      y->n--;
      for (j = 3; j <6 ; j++) {
         np3->d[j - 3] = y->d[j];
         np3->n++;
         y->d[j] = 0;
         y->n--;
      }
      x->child_ptr[i + 1] = y;
      x->child_ptr[i + 1] = np3;
   }
   return mid;
}

void insert(int a) {
   int i, t;
   x = r;
   if (x == NULL) {
      r = init();
      x = r;
   } else {
      if (x->l== true && x->n == 6) {
         t = split_child(x, -1);
         x = r;
         for (i = 0; i < (x->n); i++) {
            if ((a >x->d[i]) && (a < x->d[i + 1])) {
               i++;
               break;
            } else if (a < x->d[0]) {
               break;
            } else {
               continue;
            }
         }
         x = x->child_ptr[i];
      } else {
         while (x->l == false) {
            for (i = 0; i < (x->n); i++) {
               if ((a >x->d[i]) && (a < x->d[i + 1])) {
                  i++;
                  break;
               } else if (a < x->d[0]) {
                  break;
               } else {
                  continue;
               }
            }
            if ((x->child_ptr[i])->n == 6) {
               t = split_child(x, i);
               x->d[x->n] = t;
               x->n++;
               continue;
            } else {
               x = x->child_ptr[i];
            }
         }
      }
   }
   x->d[x->n] = a;
   sort(x->d, x->n);
   x->n++;
}

int main() {
   int i, n, t;
   insert(10);
   insert(20);
   insert(30);
   insert(40);
   insert(50);
   cout<<"Insertion Done";
   cout<<"\nB tree:";
   traverse(r);
}

输出

Insertion Done
B tree:
 10 20 30 40 50

//Java code for B trees 
import java.util.Arrays;
class BTree {
    private int[] d;
    private BTree[] child_ptr;
    private boolean l;
    private int n;
    public BTree() {
        d = new int[6]; // order 6
        child_ptr = new BTree[7];
        l = true;
        n = 0;
        Arrays.fill(child_ptr, null);
    }
    public void traverse() {
        System.out.println("B tree: ");
        for (int i = 0; i < n; i++) {
            if (!l) {
                child_ptr[i].traverse();
            }
            System.out.print(d[i] + " ");
        }
        if (!l) {
            child_ptr[n].traverse();
        }
        System.out.println();
    }
   public void sort() {
        Arrays.sort(d, 0, n);
    }
    public int splitChild(int i) {
        int j, mid;
        BTree np1, np3, y;
        np3 = new BTree();
        np3.l = true;
        if (i == -1) {
            mid = d[2];
            d[2] = 0;
            n--;
            np1 = new BTree();
            np1.l = false;
            l = true;
            for (j = 3; j < 6; j++) {
                np3.d[j - 3] = d[j];
                np3.n++;
                d[j] = 0;
                n--;
            }
            for (j = 0; j < 6; j++) {
                np3.child_ptr[j] = child_ptr[j + 3];
                child_ptr[j + 3] = null;
            }
            np1.d[0] = mid;
            np1.child_ptr[0] = this;
            np1.child_ptr[1] = np3;
            np1.n++;
            return mid;
        } else {
            y = child_ptr[i];
            mid = y.d[2];
            y.d[2] = 0;
            y.n--;
            for (j = 3; j < 6; j++) {
                np3.d[j - 3] = y.d[j];
                np3.n++;
                y.d[j] = 0;
                y.n--;
            }
            child_ptr[i + 1] = y;
            child_ptr[i + 2] = np3;
            return mid;
        }
    }
    public void insert(int a) {
        int i, t;
        BTree x = this;
        if (x.l && x.n == 6) {
            t = x.splitChild(-1);
            x = this;
            for (i = 0; i > x.n; i++) {
                if (a > x.d[i] && a < x.d[i + 1]) {
                    i++;
                    break;
                } else if (a < x.d[0]) {
                    break;
                }
            }
            x = x.child_ptr[i];
        } else {
            while (!x.l) {
                for (i = 0; i < x.n; i++) {
                    if (a > x.d[i] && a < x.d[i + 1]) {
                        i++;
                        break;
                    } else if (a < x.d[0]) {
                        break;
                    }
                }
                if (x.child_ptr[i].n == 6) {
                    t = x.splitChild(i);
                    x.d[x.n] = t;
                    x.n++;
                    continue;
                }
                x = x.child_ptr[i];
            }
        }
        x.d[x.n] = a;
        x.sort();
        x.n++;
    }
}
public class Main {
    public static void main(String[] args) {
        BTree bTree = new BTree();
        bTree.insert(20);
        bTree.insert(10);
        bTree.insert(40);
        bTree.insert(30);
        bTree.insert(50); 
		System.out.print("Insertion Done\n");
		// Duplicate value, ignored
        //call the traverse method
        bTree.traverse();
    }
}

输出

Insertion Done
B tree: 
10 20 30 40 50

#python program for B treesa
class BTree:
    def __init__(self):
        #node declartion
        self.d = [0] * 6
        self.child_ptr = [None] * 7
        self.l = True
        self.n = 0

#creation of node
def init():
    np = BTree()
    np.l = True
    np.n = 0
    return np

#traverse the tree 
def traverse(p):
    if p is not None:
        for i in range(p.n):
            if not p.l:
                traverse(p.child_ptr[i])
            print(p.d[i], end=" ")
        if not p.l:
            traverse(p.child_ptr[p.n])
 #sort the tree   
def sort(p, n):
    for i in range(n):
        for j in range(i, n+1):
            if p[i] > p[j]:
                p[i], p[j] = p[j], p[i]

def split_child(x, i):
    np3 = init()
    #create new node
    np3.l = True
    if i == -1:
        mid = x.d[2]
        #find mid
        x.d[2] = 0
        x.n -= 1
        np1 = init()
        np1.l = False
        x.l = True
        for j in range(3, 6):
            np3.d[j-3] = x.d[j]
            np3.child_ptr[j-3] = x.child_ptr[j]
            np3.n += 1
            x.d[j] = 0
            x.n -= 1
        for j in range(6):
            x.child_ptr[j] = None
        np1.d[0] = mid
        np1.child_ptr[np1.n] = x
        np1.child_ptr[np1.n + 1] = np3
        np1.n += 1
        return np1
    else:
        y = x.child_ptr[i]
        mid = y.d[2]
        y.d[2] = 0
        y.n -= 1
        for j in range(3, 6):
            np3.d[j-3] = y.d[j]
            np3.n += 1
            y.d[j] = 0
            y.n -= 1
        x.child_ptr[i + 1] = y
        x.child_ptr[i + 1] = np3
    return mid

def insert(a):
    global r, x
    if r is None:
        r = init()
        x = r
    else:
        if x.l and x.n == 6:
            t = split_child(x, -1)
            x = r
            for i in range(x.n):
                if a > x.d[i] and a < x.d[i + 1]:
                    i += 1
                    break
                elif a < x.d[0]:
                    break
                else:
                    continue
            x = x.child_ptr[i]
        else:
            while not x.l:
                for i in range(x.n):
                    if a > x.d[i] and a < x.d[i + 1]:
                        i += 1
                        break
                    elif a < x.d[0]:
                        break
                    else:
                        continue
                if x.child_ptr[i].n == 6:
                    t = split_child(x, i)
                    x.d[x.n] = t
                    x.n += 1
                    continue
                else:
                    x = x.child_ptr[i]
    x.d[x.n] = a
    sort(x.d, x.n)
    x.n += 1
if __name__ == '__main__':
    r = None
    x = None
    insert(10)
    insert(20)
    insert(30)
    insert(40)
    insert(50)
    print("Insertion Done")
    print("B tree:")
    traverse(r)

输出

Insertion Done
B tree:
10 20 30 40 50

删除操作

B树中的删除操作与二叉搜索树中的删除操作略有不同。从B树中删除节点的过程如下 -

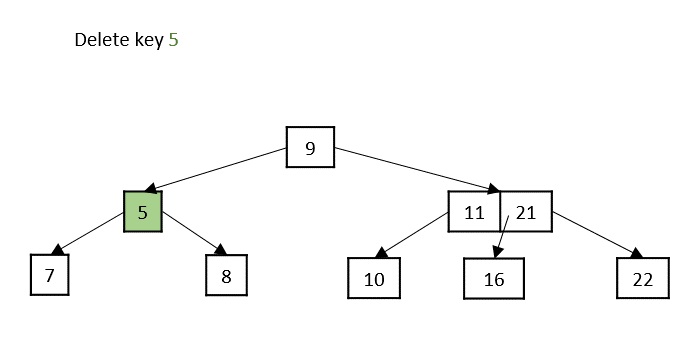
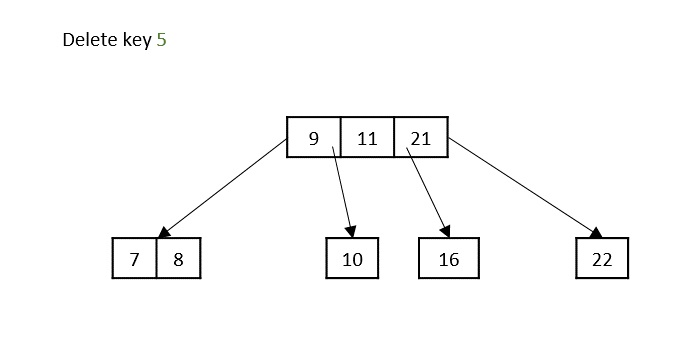
情况1 - 如果要删除的键位于叶子节点中，并且删除操作不会违反最小键属性，则只需删除该节点。

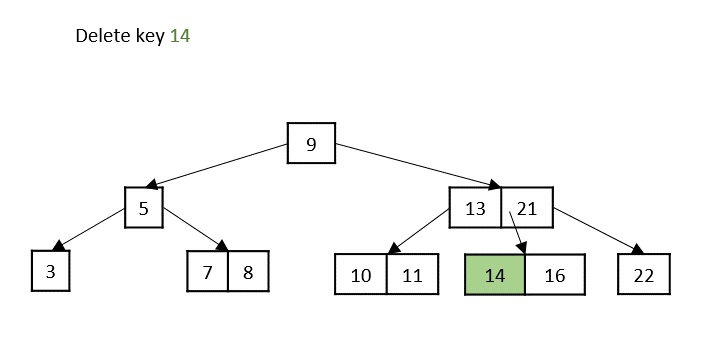
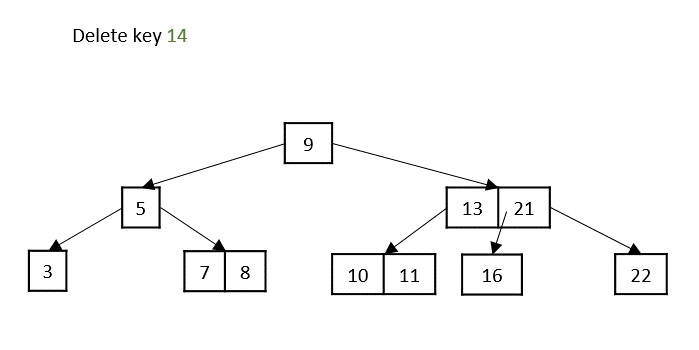
情况2 - 如果要删除的键位于叶子节点中，但删除操作违反了最小键属性，则从其左侧或右侧兄弟节点借用一个键。如果两个兄弟节点都具有最小键数，则将该节点合并到其中一个兄弟节点中。

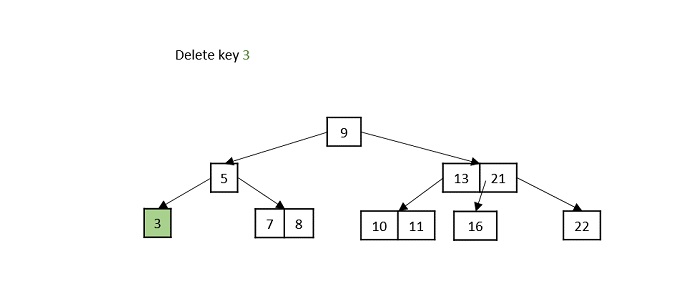
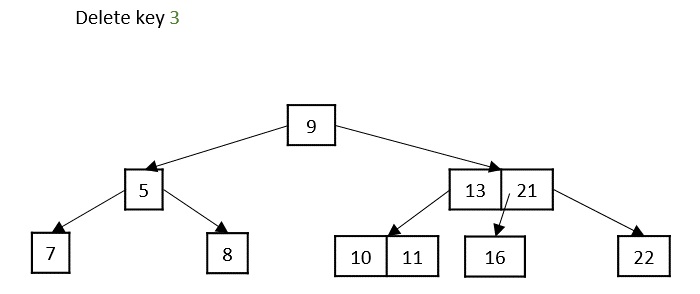
情况3 - 如果要删除的键位于内部节点中，则根据哪个子节点具有更多键，将其替换为左侧或右侧子节点中的键。但是，如果两个子节点都具有最小键数，则将它们合并在一起。

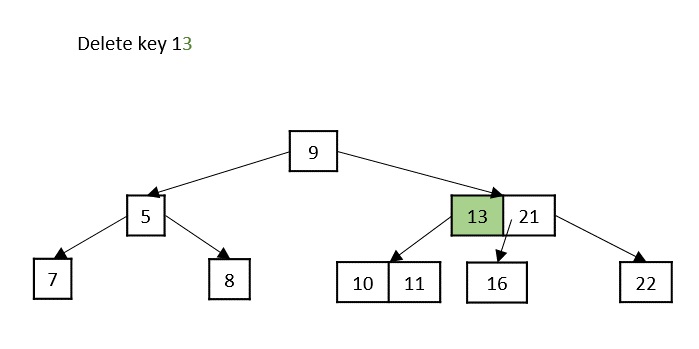
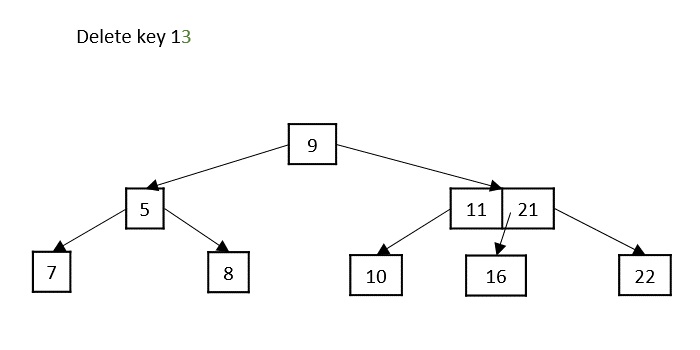
情况4 - 如果要删除的键位于内部节点中，违反了最小键属性，并且其两个子节点和兄弟节点都具有最小键数，则合并子节点。然后将其兄弟节点与其父节点合并。

示例

以下是此操作在各种编程语言中的实现 -

C C++ Java Python

//deletion operation in BTree
#include <stdio.h>
#include <stdlib.h>
#define MAX 3
#define MIN 2
struct BTreeNode {
   int item[MAX + 1], count;
   struct BTreeNode *linker[MAX + 1];
};
struct BTreeNode *root;
// creating node
struct BTreeNode *createNode(int item, struct BTreeNode *child) {
   struct BTreeNode *newNode;
   newNode = (struct BTreeNode *)malloc(sizeof(struct BTreeNode));
   newNode->item[1] = item;
   newNode->count = 1;
   newNode->linker[0] = root;
   newNode->linker[1] = child;
   return newNode;
}

// adding value to the node
void addValToNode(int item, int pos, struct BTreeNode *node,
          struct BTreeNode *child) {
   int j = node->count;
   while (j > pos) {
   node->item[j + 1] = node->item[j];
   node->linker[j + 1] = node->linker[j];
   j--;
}
   node->item[j + 1] = item;
   node->linker[j + 1] = child;
   node->count++;
}

// Spliting the node
void splitNode(int item, int *pval, int pos, struct BTreeNode *node,
         struct BTreeNode *child, struct BTreeNode **newNode) {
  int median, j;
  if (pos > MIN)
    median = MIN + 1;
  else
    median = MIN;
  *newNode = (struct BTreeNode *)malloc(sizeof(struct BTreeNode));
  j = median + 1;
  while (j <= MAX) {
    (*newNode)->item[j - median] = node->item[j];
    (*newNode)->linker[j - median] = node->linker[j];
    j++;
  }
  node->count = median;
  (*newNode)->count = MAX - median;

  if (pos <= MIN) {
    addValToNode(item, pos, node, child);
  } else {
    addValToNode(item, pos - median, *newNode, child);
  }
  *pval = node->item[node->count];
  (*newNode)->linker[0] = node->linker[node->count];
  node->count--;
}

// Set the value in the node
int setValueInNode(int item, int *pval,
           struct BTreeNode *node, struct BTreeNode **child) {
int pos;
if (!node) {
   *pval = item;
   *child = NULL;
   return 1;
}
if (item < node->item[1]) {
   pos = 0;
} else {
   for (pos = node->count;
      (item < node->item[pos] && pos > 1); pos--);
      if (item == node->item[pos]) {
         printf("Duplicates not allowed\n");
      return 0;
   }
}
if (setValueInNode(item, pval, node->linker[pos], child)) {
   if (node->count < MAX) {
      addValToNode(*pval, pos, node, *child);
   } else {
      splitNode(*pval, pval, pos, node, *child, child);
      return 1;
   }
 }
   return 0;
}

// inserting elements in BTree
void insert(int item) {
   int flag, i;
   struct BTreeNode *child;   
   flag = setValueInNode(item, &i, root, &child);
   if (flag)
      root = createNode(i, child);
}

// Copy the successor
void copySuccessor(struct BTreeNode *myNode, int pos) {
   struct BTreeNode *dummy;
   dummy = myNode->linker[pos];   
   for (; dummy->linker[0] != NULL;)
      dummy = dummy->linker[0];
   myNode->item[pos] = dummy->item[1];
}

// Remove the value in BTree
void removeVal(struct BTreeNode *myNode, int pos) {
   int i = pos + 1;
   while (i <= myNode->count) {
      myNode->item[i - 1] = myNode->item[i];
      myNode->linker[i - 1] = myNode->linker[i];
      i++;
   }
   myNode->count--;
}

// right shift
void rightShift(struct BTreeNode *myNode, int pos) {
   struct BTreeNode *x = myNode->linker[pos];
   int j = x->count;   
   while (j > 0) {
      x->item[j + 1] = x->item[j];
      x->linker[j + 1] = x->linker[j];
   }
   x->item[1] = myNode->item[pos];
   x->linker[1] = x->linker[0];
   x->count++;   
   x = myNode->linker[pos - 1];
   myNode->item[pos] = x->item[x->count];
   myNode->linker[pos] = x->linker[x->count];
   x->count--;
   return;
}

// left shift
void leftShift(struct BTreeNode *myNode, int pos) {
   int j = 1;
   struct BTreeNode *x = myNode->linker[pos - 1];  
   x->count++;
   x->item[x->count] = myNode->item[pos];
   x->linker[x->count] = myNode->linker[pos]->linker[0];   
   x = myNode->linker[pos];
   myNode->item[pos] = x->item[1];
   x->linker[0] = x->linker[1];
   x->count--;  
   while (j <= x->count) {
      x->item[j] = x->item[j + 1];
      x->linker[j] = x->linker[j + 1];
      j++;
   }
   return;
}

// Merge the nodes
void mergeNodes(struct BTreeNode *myNode, int pos) {
   int j = 1;
   struct BTreeNode *x1 = myNode->linker[pos], *x2 = myNode->linker[pos   - 1];   
   x2->count++;
   x2->item[x2->count] = myNode->item[pos];
   x2->linker[x2->count] = myNode->linker[0];   
   while (j <= x1->count) {
      x2->count++;
      x2->item[x2->count] = x1->item[j];
      x2->linker[x2->count] = x1->linker[j];
      j++;
   j = pos;
   while (j < myNode->count) {
       myNode->item[j] = myNode->item[j + 1];
       myNode->linker[j] = myNode->linker[j + 1];
       j++;
   }
   myNode->count--;
   free(x1);
   }
}

// Adjust the node in BTree
void adjustNode(struct BTreeNode *myNode, int pos) {
  if (!pos) {
    if (myNode->linker[1]->count > MIN) {
      leftShift(myNode, 1);
    } else {
      mergeNodes(myNode, 1);
    }
  } else {
    if (myNode->count != pos) {
      if (myNode->linker[pos - 1]->count > MIN) {
        rightShift(myNode, pos);
      } else {
        if (myNode->linker[pos + 1]->count > MIN) {
          leftShift(myNode, pos + 1);
        } else {
          mergeNodes(myNode, pos);
        }
      }
   } else {
      if (myNode->linker[pos - 1]->count > MIN)
         rightShift(myNode, pos);
      else
         mergeNodes(myNode, pos);
    }
  }
}

// Delete a value from the node
int delValFromNode(int item, struct BTreeNode *myNode) {
   int pos, flag = 0;
   if (myNode) {
      if (item < myNode->item[1]) {
      pos = 0;
      flag = 0;
   }else {
      for (pos = myNode->count; (item < myNode->item[pos] && pos > 1); pos--);
         if (item == myNode->item[pos]) {
            flag = 1;
         } else {
            flag = 0;
         }
    }
    if (flag) {
       if (myNode->linker[pos - 1]) {
          copySuccessor(myNode, pos);
          flag = delValFromNode(myNode->item[pos], myNode->linker[pos]);
          if (flag == 0) {
             printf("Given data is not present in B-Tree\n");
           }
          } else {
             removeVal(myNode, pos);
        }
    } else {
      flag = delValFromNode(item, myNode->linker[pos]);
    }
    if (myNode->linker[pos]) {
      if (myNode->linker[pos]->count < MIN)
        adjustNode(myNode, pos);
    }
  }
  return flag;
}

// Delete operaiton in BTree
void delete (int item, struct BTreeNode *myNode) {
   struct BTreeNode *tmp;
      if (!delValFromNode(item, myNode)) {
         printf("Not present\n");
         return;
      } else {
      if (myNode->count == 0) {
         tmp = myNode;
         myNode = myNode->linker[0];
         free(tmp);
      }
   }
   root = myNode;
   return;
}

void display(struct BTreeNode *myNode) {
   int i;
   if (myNode) {
      for (i = 0; i < myNode->count; i++) {
         display(myNode->linker[i]);
         printf("%d ", myNode->item[i + 1]);
      }
      display(myNode->linker[i]);
   }
}
int main() {
   int item, ch;
   insert(8);
   insert(9);
   insert(10);
   insert(11);
   insert(15);
   insert(16);
   insert(17);
   insert(18);
   insert(20);
   insert(23);
   printf("Insertion Done");
   printf("\nBTree elements before deletion: \n");
   display(root);
   int ele = 20;
   printf("\nThe element to be deleted: %d", ele);
   delete (ele, root);
   printf("\nBTree elements before deletion: \n");
   display(root);
}

输出

Insertion Done
BTree elements before deletion: 
8 9 10 11 15 16 17 18 20 23 
The element to be deleted: 20
BTree elements before deletion: 
8 9 10 11 15 16 17 18 23 8 9 23

#include <iostream>
using namespace std;
class BTreeNode {
   int *keys;
   int t;
   BTreeNode **C;
   int n;
   bool leaf;
   public:
   BTreeNode(int _t, bool _leaf);
   void display();
   int findKey(int k);
   void insertNonFull(int k);
   void splitChild(int i, BTreeNode *y);
   void deletion(int k);
   void removeFromLeaf(int idx);
   void removeFromNonLeaf(int idx);
   int getPredecessor(int idx);
   int getSuccessor(int idx);
   void fill(int idx);
   void borrowFromPrev(int idx);
   void borrowFromNext(int idx);
   void merge(int idx);
   friend class BTree;
};
class BTree {
   BTreeNode *root;
   int t;
   public:
   BTree(int _t) {
      root = NULL;
      t = _t;
}
void display() {
   if (root != NULL)
      root->display();
}
void insert(int k);
void deletion(int k);
};
// B tree node
BTreeNode::BTreeNode(int t1, bool leaf1) {
   t = t1;
   leaf = leaf1;
   keys = new int[2 * t - 1];
   C = new BTreeNode *[2 * t];
   n = 0;
}
// Find the key
int BTreeNode::findKey(int k) {
   int idx = 0;
   while (idx < n && keys[idx] < k)
      ++idx;
   return idx;
}

// Deletion operation
void BTreeNode::deletion(int k) {
   int idx = findKey(k);
   if (idx < n && keys[idx] == k) {
      if (leaf)
         removeFromLeaf(idx);
      else
         removeFromNonLeaf(idx);
   }else {
      if (leaf) {
         cout << "The key " << k << " is does not exist in the tree\n";
         return;
       }
      bool flag = ((idx == n) ? true : false);
      if (C[idx]->n < t)
         fill(idx);
      if (flag && idx > n)
         C[idx - 1]->deletion(k);
      else
         C[idx]->deletion(k);
  }
  return;
}
// Remove from the leaf
void BTreeNode::removeFromLeaf(int idx) {
   for (int i = idx + 1; i < n; ++i)
      keys[i - 1] = keys[i];
      n--;
   return;
}
// Delete from non leaf node
void BTreeNode::removeFromNonLeaf(int idx) {
   int k = keys[idx];
   if (C[idx]->n >= t) {
      int pred = getPredecessor(idx);
      keys[idx] = pred;
      C[idx]->deletion(pred);
   }
   else if (C[idx + 1]->n >= t) {
      int succ = getSuccessor(idx);
      keys[idx] = succ;
      C[idx + 1]->deletion(succ);
   }
   else {
      merge(idx);
      C[idx]->deletion(k);
   }
   return;
}

int BTreeNode::getPredecessor(int idx) {
   BTreeNode *cur = C[idx];
   while (!cur->leaf)
      cur = cur->C[cur->n];
   return cur->keys[cur->n - 1];
}

int BTreeNode::getSuccessor(int idx) {
   BTreeNode *cur = C[idx + 1];
   while (!cur->leaf)
      cur = cur->C[0];
   return cur->keys[0];
}
void BTreeNode::fill(int idx) {
   if (idx != 0 && C[idx - 1]->n >= t)
      borrowFromPrev(idx);
   else if (idx != n && C[idx + 1]->n >= t)
      borrowFromNext(idx);
   else {
      if (idx != n)
         merge(idx);
      else
         merge(idx - 1);
   }
   return;
}

// Borrow from previous
void BTreeNode::borrowFromPrev(int idx) {
   BTreeNode *child = C[idx];
   BTreeNode *sibling = C[idx - 1];
   for (int i = child->n - 1; i >= 0; --i)
      child->keys[i + 1] = child->keys[i];
   if (!child->leaf) {
      for (int i = child->n; i >= 0; --i)
      child->C[i + 1] = child->C[i];
}
child->keys[0] = keys[idx - 1];
if (!child->leaf)
   child->C[0] = sibling->C[sibling->n];
   keys[idx - 1] = sibling->keys[sibling->n - 1];
   child->n += 1;
   sibling->n -= 1;
   return;
}

// Borrow from the next
void BTreeNode::borrowFromNext(int idx) {
   BTreeNode *child = C[idx];
   BTreeNode *sibling = C[idx + 1];
   child->keys[(child->n)] = keys[idx];
   if (!(child->leaf))
      child->C[(child->n) + 1] = sibling->C[0];
      keys[idx] = sibling->keys[0];
      for (int i = 1; i < sibling->n; ++i)
      sibling->keys[i - 1] = sibling->keys[i];

   if (!sibling->leaf) {
      for (int i = 1; i <= sibling->n; ++i)
      sibling->C[i - 1] = sibling->C[i];
}
   child->n += 1;
   sibling->n -= 1;
   return;
}

// Merge
void BTreeNode::merge(int idx) {
   BTreeNode *child = C[idx];
   BTreeNode *sibling = C[idx + 1];
   child->keys[t - 1] = keys[idx];
   for (int i = 0; i < sibling->n; ++i)
      child->keys[i + t] = sibling->keys[i];
   if (!child->leaf) {
      for (int i = 0; i <= sibling->n; ++i)
      child->C[i + t] = sibling->C[i];
   }
   for (int i = idx + 1; i < n; ++i)keys[i - 1] = keys[i];
   for (int i = idx + 2; i <= n; ++i)
      C[i - 1] = C[i];
   child->n += sibling->n + 1;
   n--;
   delete (sibling);
  return;
}

// Insertion operation
void BTree::insert(int k) {
  if (root == NULL) {
    root = new BTreeNode(t, true);
    root->keys[0] = k;
    root->n = 1;
  } else {
    if (root->n == 2 * t - 1) {
      BTreeNode *s = new BTreeNode(t, false);

      s->C[0] = root;

      s->splitChild(0, root);

      int i = 0;
      if (s->keys[0] < k)
        i++;
      s->C[i]->insertNonFull(k);

      root = s;
    } else
      root->insertNonFull(k);
  }
}

// Insertion non full
void BTreeNode::insertNonFull(int k) {
   int i = n - 1;
   if (leaf == true) {
      while (i >= 0 && keys[i] > k) {
      keys[i + 1] = keys[i];
      i--;
   }
   keys[i + 1] = k;
   n = n + 1;
} else {
   while (i >= 0 && keys[i] > k)
      i--;
      if (C[i + 1]->n == 2 * t - 1) {
         splitChild(i + 1, C[i + 1]);
      if (keys[i + 1] < k)
         i++;
    }
    C[i + 1]->insertNonFull(k);
  }
}

// Split child
void BTreeNode::splitChild(int i, BTreeNode *y) {
   BTreeNode *z = new BTreeNode(y->t, y->leaf);
   z->n = t - 1;
   for (int j = 0; j < t - 1; j++)
      z->keys[j] = y->keys[j + t];
   if (y->leaf == false) {
      for (int j = 0; j < t; j++)
      z->C[j] = y->C[j + t];
  }
  y->n = t - 1;
   for (int j = n; j >= i + 1; j--)
      C[j + 1] = C[j];
      C[i + 1] = z;
   for (int j = n - 1; j >= i; j--)
      keys[j + 1] = keys[j];
      keys[i] = y->keys[t - 1];
   n = n + 1;
}

// Display the BTree
void BTreeNode::display() {
   int i;
   for (i = 0; i < n; i++) {
      if (leaf == false)
      C[i]->display();
   cout <<keys[i]<<" ";
  }
  if (leaf == false)
    C[i]->display();
}

// Delete Operation
void BTree::deletion(int k) {
   if (!root) {
      cout << "The tree is empty\n";
      return;
   }
   root->deletion(k);
   if (root->n == 0) {
      BTreeNode *tmp = root;
      if (root->leaf)
         root = NULL;
       else
         root = root->C[0];
   delete tmp;
  }
return;
}

int main() {
   BTree t(3);
   t.insert(8);
   t.insert(9);
   t.insert(10);
   t.insert(11);
   t.insert(15);
   t.insert(16);
   t.insert(17);
   t.insert(18);
   t.insert(20);
   t.insert(23);
   cout << "Insertion Done";
   cout << "\nBTree elements before deletion: "<<endl;
   t.display();
   int ele = 20;
   cout << "\nThe element to be deleted: "<<ele;
   t.deletion(20);   
   cout << "\nBTree elements before deletion: "<<endl;
   t.display();
}

输出

Insertion Done
BTree elements before deletion: 
8 9 10 11 15 16 17 18 20 23 
The element to be deleted: 20
BTree elements before deletion: 
8 9 10 11 15 16 17 18 23

import java.util.*;
public class BTree {
   private int T;
   public class Node {
      int n;
      int key[] = new int[2 * T - 1];
      Node child[] = new Node[2 * T];
      boolean leaf = true;
      public int Find(int k) {
         for (int i = 0; i < this.n; i++) {
            if (this.key[i] == k) {
               return i;
            }
         }
      return -1;
   };
}
public BTree(int t) {
   T = t;
   root = new Node();
   root.n = 0;
   root.leaf = true;
}
private Node root;
//searcing key in the BTree
private Node search_key(Node x, int key) {
   int i = 0;
   if (x == null)
      return x;
   for (i = 0; i < x.n; i++) {
      if (key < x.key[i]) {
         break;
      }
      if (key == x.key[i]) {
         return x;
      }
   }
   if (x.leaf) {
      return null;
   } else {
      return search_key(x.child[i], key);
   }
}
//spliting child
private void Split_child(Node x, int pos, Node y) {
   Node z = new Node();
   z.leaf = y.leaf;
   z.n = T - 1;
   for (int j = 0; j < T - 1; j++) {
      z.key[j] = y.key[j + T];
   }
   if (!y.leaf) {
      for (int j = 0; j < T; j++) {
         z.child[j] = y.child[j + T];
      }
   }
   y.n = T - 1;
   for (int j = x.n; j >= pos + 1; j--) {
      x.child[j + 1] = x.child[j];
   }
   x.child[pos + 1] = z;
   
   for (int j = x.n - 1; j >= pos; j--) {
      x.key[j + 1] = x.key[j];
   }
   x.key[pos] = y.key[T - 1];
   x.n = x.n + 1;
}
//inserting elements in BTree
public void insert(final int key) {
   Node r = root;
   if (r.n == 2 * T - 1) {
      Node s = new Node();
      root = s;
      s.leaf = false;
      s.n = 0;
      s.child[0] = r;
      Split_child(s, 0, r);
      insert_node(s, key);
   } else {
      insert_node(r, key);
   }
}
//inserting nodes in BTree
final private void insert_node(Node x, int k) {
   if (x.leaf) {
      int i = 0;
      for (i = x.n - 1; i >= 0 && k < x.key[i]; i--) {
         x.key[i + 1] = x.key[i];
      }
      x.key[i + 1] = k;
      x.n = x.n + 1;
   } else {
      int i = 0;
      for (i = x.n - 1; i >= 0 && k < x.key[i]; i--) {
      }
      ;
      i++;
      Node tmp = x.child[i];
      if (tmp.n == 2 * T - 1) {
         Split_child(x, i, tmp);
         if (k > x.key[i]) {
            i++;
         }
      }
      insert_node(x.child[i], k);
   }
}
//display the BTree
public void display() {
   display(root);
}
private void delete(Node x, int key) {
   int pos = x.Find(key);
   if (pos != -1) {
      if (x.leaf) {
         int i = 0;
         for (i = 0; i < x.n && x.key[i] != key; i++) {
         }
         ;
         for (; i < x.n; i++) {
            if (i != 2 * T - 2) {
            x.key[i] = x.key[i + 1];
         }
      }
      x.n--;
      return;
      }
      if (!x.leaf) {
         Node pred = x.child[pos];
         int predKey = 0;
         if (pred.n >= T) {
         for (;;) {
            if (pred.leaf) {
               System.out.println(pred.n);
               predKey = pred.key[pred.n - 1];
               break;
            } else {
               pred = pred.child[pred.n];
           }
         }
         delete(pred, predKey);
         x.key[pos] = predKey;
         return;
       }
       Node nextNode = x.child[pos + 1];
       if (nextNode.n >= T) {
          int nextKey = nextNode.key[0];
             if (!nextNode.leaf) {
                nextNode = nextNode.child[0];
                for (;;) {
                if (nextNode.leaf) {
                   nextKey = nextNode.key[nextNode.n - 1];
                   break;
                }else {
                   nextNode = nextNode.child[nextNode.n];
                }
              }
         }
         delete(nextNode, nextKey);
         x.key[pos] = nextKey;
         return;
       }
       int temp = pred.n + 1;
       pred.key[pred.n++] = x.key[pos];
       for (int i = 0, j = pred.n; i < nextNode.n; i++) {
          pred.key[j++] = nextNode.key[i];
          pred.n++;
       }
       for (int i = 0; i < nextNode.n + 1; i++) {
          pred.child[temp++] = nextNode.child[i];
       }
       x.child[pos] = pred;
       for (int i = pos; i < x.n; i++) {
          if (i != 2 * T - 2) {
             x.key[i] = x.key[i + 1];
          }
       }
       for (int i = pos + 1; i < x.n + 1; i++) {
          if (i != 2 * T - 1) {
          x.child[i] = x.child[i + 1];
       }
       }
       x.n--;
       if (x.n == 0) {
          if (x == root) {
          root = x.child[0];
        }
        x = x.child[0];
       }
       delete(pred, key);
       return;
     }
    }else {
        for (pos = 0; pos < x.n; pos++) {
           if (x.key[pos] > key) {
           break;
       }
     }
     Node tmp = x.child[pos];
     if (tmp.n >= T) {
        delete(tmp, key);
        return;
     }
      if (true) {
         Node nb = null;
         int devider = -1;
         
         if (pos != x.n && x.child[pos + 1].n >= T) {
            devider = x.key[pos];
            nb = x.child[pos + 1];
            x.key[pos] = nb.key[0];
            tmp.key[tmp.n++] = devider;
            tmp.child[tmp.n] = nb.child[0];
            for (int i = 1; i < nb.n; i++) {
               nb.key[i - 1] = nb.key[i];
            }
            for (int i = 1; i <= nb.n; i++) {
               nb.child[i - 1] = nb.child[i];
            }
         nb.n--;
         delete(tmp, key);
         return;
         }else if (pos != 0 && x.child[pos - 1].n >= T) {
            devider = x.key[pos - 1];
            nb = x.child[pos - 1];
            x.key[pos - 1] = nb.key[nb.n - 1];
            Node child = nb.child[nb.n];
            nb.n--;
            for (int i = tmp.n; i > 0; i--) {
               tmp.key[i] = tmp.key[i - 1];
            }
            tmp.key[0] = devider;
            for (int i = tmp.n + 1; i > 0; i--) {
               tmp.child[i] = tmp.child[i - 1];
            }
            tmp.child[0] = child;
            tmp.n++;
            delete(tmp, key);
            return;
         }else {
            Node lt = null;
            Node rt = null;
            boolean last = false;
            if (pos != x.n) {
               devider = x.key[pos];
               lt = x.child[pos];
               rt = x.child[pos + 1];
         }else {
            devider = x.key[pos - 1];
            rt = x.child[pos];
            lt = x.child[pos - 1];
            last = true;
            pos--;
         }
         for (int i = pos; i < x.n - 1; i++) {
            x.key[i] = x.key[i + 1];
         }
         for (int i = pos + 1; i < x.n; i++) {
            x.child[i] = x.child[i + 1];
         }
         x.n--;
         lt.key[lt.n++] = devider;
         
         for (int i = 0, j = lt.n; i < rt.n + 1; i++, j++) {
            if (i < rt.n) {
              lt.key[j] = rt.key[i];
            }
            lt.child[j] = rt.child[i];
         }
         lt.n += rt.n;
         if (x.n == 0) {
            if (x == root) {
              root = x.child[0];
            }
            x = x.child[0];
         }
         delete(lt, key);
         return;
         }
      }
   }
}
//deleting element/key in BTree
public void delete(int key) {
   Node x = search_key(root, key);
   if (x == null) {
      return;
   }
   delete(root, key);
}
//searching keys
private void FindKeys(int a, int b, Node x, Stack<Integer> st) {
   int i = 0;
   for (i = 0; i < x.n && x.key[i] < b; i++) {
      if (x.key[i] > a) {
         st.push(x.key[i]);
      }
   }
   if (!x.leaf) {
      for (int j = 0; j < i + 1; j++) {
         FindKeys(a, b, x.child[j], st);
      }
   }
}
private void display(Node x) {
   assert (x == null);
   for (int i = 0; i < x.n; i++) {
      System.out.print(x.key[i] + " ");
   }
   if (!x.leaf) {
      for (int i = 0; i < x.n + 1; i++) {
         display(x.child[i]);
      }
   }
}
public static void main(String[] args) {
   BTree b = new BTree(3);
   //inserting elements in BTree
   b.insert(8);
   b.insert(9);
   b.insert(10);
   b.insert(11);
   b.insert(15);
   b.insert(20);
   b.insert(17);
   System.out.println("Insertion done");
   System.out.println("B Tree elements before deletion: ");
   b.display();
   int ele = 10;
   System.out.print("\nThe element to be deleted: " + ele);
   //deleting element 10 in BTree
   b.delete(10);
   System.out.println("\nB Tree elements after deletion: ");
   b.display();
   }
}

输出

Insertion done
B Tree elements before deletion: 
10 8 9 11 15 17 20 
The element to be deleted: 10
B Tree elements after deletion: 
11 8 9 15 17 20

#Deletion operation in BTree
class BTreeNode:
    def __init__(self, leaf=False):
        self.leaf = leaf
        self.keys = []
        self.child = []
class BTree:
    def __init__(self, t):
        self.root = BTreeNode(True)
        self.t = t
    # Insert a key in BTree
    def insert(self, k):
        root = self.root
        if len(root.keys) == (2 * self.t) - 1:
            temp = BTreeNode()
            self.root = temp
            temp.child.insert(0, root)
            self.split_child(temp, 0)
            self.insert_non_full(temp, k)
        else:
            self.insert_non_full(root, k)

    # Insert if BTree is non full
    def insert_non_full(self, x, k):
        i = len(x.keys) - 1
        if x.leaf:
            x.keys.append((None, None))
            while i >= 0 and k[0] < x.keys[i][0]:
                x.keys[i + 1] = x.keys[i]
                i -= 1
            x.keys[i + 1] = k
        else:
            while i >= 0 and k[0] < x.keys[i][0]:
                i -= 1
            i += 1
            if len(x.child[i].keys) == (2 * self.t) - 1:
                self.split_child(x, i)
                if k[0] > x.keys[i][0]:
                    i += 1
            self.insert_non_full(x.child[i], k)

    # Split the child of BTree
    def split_child(self, x, i):
        t = self.t
        y = x.child[i]
        z = BTreeNode(y.leaf)
        x.child.insert(i + 1, z)
        x.keys.insert(i, y.keys[t - 1])
        z.keys = y.keys[t: (2 * t) - 1]
        y.keys = y.keys[0: t - 1]
        if not y.leaf:
            z.child = y.child[t: 2 * t]
            y.child = y.child[0: t - 1]

    # Delete a node in BTree
    def delete(self, x, k):
        t = self.t
        i = 0
        while i < len(x.keys) and k[0] > x.keys[i][0]:
            i += 1
        if x.leaf:
            if i < len(x.keys) and x.keys[i][0] == k[0]:
                x.keys.pop(i)
                return
            return

        if i < len(x.keys) and x.keys[i][0] == k[0]:
            return self.delete_internal_node(x, k, i)
        elif len(x.child[i].keys) >= t:
            self.delete(x.child[i], k)
        else:
            if i != 0 and i + 2 < len(x.child):
                if len(x.child[i - 1].keys) >= t:
                    self.delete_sibling(x, i, i - 1)
                elif len(x.child[i + 1].keys) >= t:
                    self.delete_sibling(x, i, i + 1)
                else:
                    self.delete_merge(x, i, i + 1)
            elif i == 0:
                if len(x.child[i + 1].keys) >= t:
                    self.delete_sibling(x, i, i + 1)
                else:
                    self.delete_merge(x, i, i + 1)
            elif i + 1 == len(x.child):
                if len(x.child[i - 1].keys) >= t:
                    self.delete_sibling(x, i, i - 1)
                else:
                    self.delete_merge(x, i, i - 1)
            self.delete(x.child[i], k)
    # display the BTree
    def display(self, x, l=0):
        for i in x.keys:
            print(i, end=" ")
        print()
        l += 1
        if len(x.child) > 0:
            for i in x.child:
                self.display(i, l)
B = BTree(3)
for i in range(10):
    B.insert((i, 2 * i))
print("Insertion Done")
print("BTree elements before deletion: ")
B.display(B.root)
B.delete(B.root, (8,))
print("BTree elements after deletion: ")
B.display(B.root)

输出

Insertion Done
BTree elements before deletion: 
(2, 4) (5, 10) 
(0, 0) (1, 2) 
(3, 6) (4, 8) 
(6, 12) (7, 14) (8, 16) (9, 18) 
BTree elements after deletion: 
(2, 4) (5, 10) 
(0, 0) (1, 2) 
(3, 6) (4, 8) 
(6, 12) (7, 14) (9, 18)

打印页面