二分查找算法

Table of content
上一页
下一页

二分查找是一种快速搜索算法，其运行时间复杂度为O(log n)。这种搜索算法基于分治的思想，因为它在搜索前将数组分成两半。为了使该算法正常工作，数据集合必须已排序。

二分查找通过比较集合中最中间的项目来查找特定的键值。如果匹配成功，则返回项目的索引。但如果中间项的值大于键值，则搜索中间项的右子数组。否则，搜索左子数组。这个过程递归地继续进行，直到子数组的大小减小到零。

binary_search_algorithm

二分查找算法

二分查找算法是一种区间搜索方法，它只在区间内执行搜索。二分查找算法的输入必须始终是一个已排序的数组，因为它根据大于或小于的值将数组划分为子数组。算法遵循以下步骤：

步骤1 - 选择数组中的中间项，并将其与要搜索的键值进行比较。如果匹配，则返回中位数的位置。

步骤2 - 如果它与键值不匹配，则检查键值是否大于或小于中位数。

步骤3 - 如果键值较大，则在右子数组中执行搜索；但如果键值小于中位数，则在左子数组中执行搜索。

步骤4 - 迭代地重复步骤1、2和3，直到子数组的大小变为1。

步骤5 - 如果键值不存在于数组中，则算法返回搜索失败。

伪代码

二分查找算法的伪代码如下所示：

Procedure binary_search
   A ← sorted array
   n ← size of array
   x ← value to be searched

   Set lowerBound = 1
   Set upperBound = n

   while x not found
      if upperBound < lowerBound
         EXIT: x does not exists.

      set midPoint = lowerBound + ( upperBound - lowerBound ) / 2

      if A[midPoint] < x
         set lowerBound = midPoint + 1

      if A[midPoint] > x
         set upperBound = midPoint - 1

      if A[midPoint] = x
         EXIT: x found at location midPoint
   end while
end procedure

分析

由于二分查找算法迭代地执行搜索，因此计算时间复杂度不像线性查找算法那样容易。

输入数组通过在每次不成功的迭代后将其划分为多个子数组来迭代地搜索。因此，形成的递归关系将是一个除法函数。

简单来说：

  • 在第一次迭代中，在整个数组中搜索元素。因此，数组长度 = n。

  • 在第二次迭代中，只搜索原始数组的一半。因此，数组长度 = n/2。

  • 在第三次迭代中，搜索前一个子数组的一半。这里，数组长度将为 = n/4。

  • 类似地，在第i次迭代中，数组长度将变为n/2i

为了实现成功的搜索，在最后一次迭代后，数组长度必须为1。因此：

n/2i = 1

这给了我们：

n = 2i

在两边应用对数，

log n = log 2i
log n = i. log 2
i = log n

二分查找算法的时间复杂度为O(log n)

示例

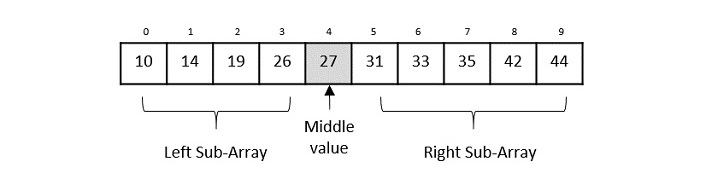
为了使二分查找工作，目标数组必须已排序。我们将通过一个图解示例学习二分查找的过程。以下是我们的已排序数组，让我们假设我们需要使用二分查找搜索值31的位置。

binary_search_with_pictorial_example

首先，我们将使用此公式确定数组的一半：

mid = low + (high - low) / 2

这里是：0 + (9 - 0) / 2 = 4（4.5的整数部分）。所以，4是数组的中点。

4th_index_array

现在我们将位置4处存储的值与要搜索的值31进行比较。我们发现位置4处的值是27，这并不匹配。由于该值大于27并且我们有一个已排序的数组，因此我们也知道目标值必须位于数组的上半部分。

location_4_value_27

我们将low更改为mid + 1，并再次找到新的mid值。

low = mid + 1
mid = low + (high - low) / 2

我们的新mid现在是7。我们将位置7处存储的值与我们的目标值31进行比较。

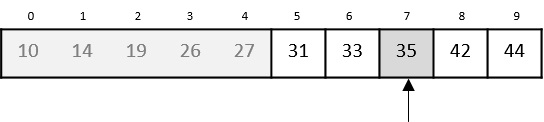
at_loaction_7

位置7处存储的值并不匹配，它小于我们正在寻找的值。因此，该值必须位于此位置的下半部分。

location_7_not_ match

因此，我们再次计算mid。这次是5。

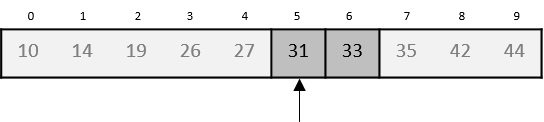
at_location_5

我们将位置5处存储的值与我们的目标值进行比较。我们发现它匹配。

location_5_matched

我们得出结论，目标值31存储在位置5。

二分查找将可搜索项减半，从而大大减少了需要进行的比较次数。

实现

二分查找是一种快速搜索算法，其运行时间复杂度为O(log n)。这种搜索算法基于分治的思想。为了使该算法正常工作，数据集合必须已排序。

C C++ Java Python
#include<stdio.h>
void binary_search(int a[], int low, int high, int key){
   int mid;
   mid = (low + high) / 2;
   if (low <= high) {
      if (a[mid] == key)
         printf("Element found at index: %d\n", mid);
      else if(key < a[mid])
         binary_search(a, low, mid-1, key);
      else if (a[mid] < key)
         binary_search(a, mid+1, high, key);
   } else if (low > high)
      printf("Unsuccessful Search\n");
}
int main(){
   int i, n, low, high, key;
   n = 5;
   low = 0;
   high = n-1;
   int a[10] = {12, 14, 18, 22, 39};
   key = 22;
   binary_search(a, low, high, key);
   key = 23;
   binary_search(a, low, high, key);
   return 0;
}

输出

Element found at index: 3
Unsuccessful Search

#include <iostream>
using namespace std;
void binary_search(int a[], int low, int high, int key){
   int mid;
   mid = (low + high) / 2;
   if (low <= high) {
      if (a[mid] == key)
         cout << "Element found at index: " << mid << endl;
      else if(key < a[mid])
         binary_search(a, low, mid-1, key);
      else if (a[mid] < key)
         binary_search(a, mid+1, high, key);
   } else if (low > high)
      cout << "Unsuccessful Search" <<endl;
}
int main(){
   int i, n, low, high, key;
   n = 5;
   low = 0;
   high = n-1;
   int a[10] = {12, 14, 18, 22, 39};
   key = 22;
   binary_search(a, low, high, key);
   key = 23;
   binary_search(a, low, high, key);
   return 0;
}

输出

Element found at index: 3
Unsuccessful Search

import java.io.*;
import java.util.*;
public class BinarySearch {
   static void binary_search(int a[], int low, int high, int key) {
      int mid = (low + high) / 2;
      if (low <= high) {
         if (a[mid] == key)
            System.out.println("Element found at index: " + mid);
         else if(key < a[mid])
            binary_search(a, low, mid-1, key);
         else if (a[mid] < key)
            binary_search(a, mid+1, high, key);
      } else if (low > high)
         System.out.println("Unsuccessful Search");
   }
   public static void main(String args[]) {
      int n, key, low, high;
      n = 5;
      low = 0;
      high = n-1;
      int a[] = {12, 14, 18, 22, 39};
      key = 22;
      binary_search(a, low, high, key);
      key = 23;
      binary_search(a, low, high, key);
   }
}

输出

Element found at index: 3
Unsuccessful Search

def binary_search(a, low, high, key):
   mid = (low + high) // 2
   if (low <= high):
      if(a[mid] == key):
         print("The element is present at index:", mid)
      elif(key < a[mid]):
         binary_search(a, low, mid-1, key)
      elif (a[mid] < key):
         binary_search(a, mid+1, high, key)
   if(low > high):
      print("Unsuccessful Search")

a = [6, 12, 14, 18, 22, 39, 55, 182]
n = len(a)
low = 0
high = n-1
key = 22
binary_search(a, low, high, key)
key = 54
binary_search(a, low, high, key)

输出

The element is present at index: 4
Unsuccessful Search
打印页面
上一页
下一页
广告