Swift程序：计算内接于正方形的圆的面积

---

本教程将讨论如何编写Swift程序来计算内接于正方形的圆的面积。

我们有一个图形，其中一个圆内接于一个正方形。这意味着圆心和正方形中心相同，圆的直径等于正方形的边长。如果我们至少有一个正方形或圆的测量值，那么我们可以很容易地计算出正方形的面积和周长，或圆的面积和周长。

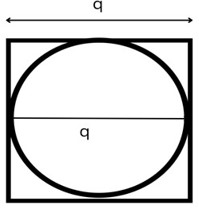
在这里，我们使用以下公式找到内接于正方形的圆的面积：

(丌/4)*q*q

这里，q是圆的半径和正方形的边长。

上述公式的推导

假设q是正方形的边长

圆的面积是πr²。

我们知道边长和圆的直径相等。所以，半径是：

r = q/2

因此，内接于正方形的圆的面积是：

A = 丌(q/2)2 = (丌/4)q2

下面是相同的演示：

输入

假设我们的给定输入是：

side = 15

输出

期望输出为：

Area of the circle inscribed in square = 176.71458676442586

算法

以下是算法：

步骤1 - 创建一个具有返回值的函数。

步骤2 - 使用以下公式找到内接于正方形的圆的面积

return (Double.pi/4) * q * q

步骤3 - 调用函数并将圆的边长作为参数传递。

步骤4 - 打印输出。

示例

以下程序演示了如何计算内接于正方形的圆的面积。

import Foundation
import Glibc

// Creating a function to find the area of

// circle inscribed in square
func inscribedCircleArea(q:Double) -> Double{
   return (Double.pi/4) * q * q
}
var num = 10.0
print("Side of the square is", num)
print("Area of the circle inscribe in square:", inscribedCircleArea(q:num))

输出

Side of the square is 10
Area of the circle inscribe in square: 78.53981633974483

在上面的程序中，我们创建了一个函数，它使用以下公式返回内接于正方形的圆的面积：

return (Double.pi/4) * q * q

这里，`Double.pi`用于访问预定义的π值。