坐标几何中三角形的面积

---

引言

坐标几何中三角形的面积用于利用坐标查找三角形的面积。在几何学中，三角形是一个有三条边和三个顶点的三边形。三角形的面积是在二维平面内三角形所覆盖的空间量。

在几何学中，三角形是一个封闭的二维图形，具有三条边、三个角和三个顶点。三角形被认为是最少边数的多边形。三角形是我们世界中具有广泛特性和应用的形状之一。三角形是一个封闭的二维图形。它们是一种多边形，其中三个角的总和通常等于180°。

在本教程中，我们将讨论坐标几何中的三角形。

三角形

在几何学中，三角形是具有三条边和三个顶点的多边形。它是二维的，具有三条直边。三角形的三个角之和等于180°。一个平面包含一个三角形。根据其边和角，三角形分为六种形式。

三角形的性质

三角形的性质有助于理解三角形各个边和角之间的关系。

• 角和性质

  根据角和性质，三角形的三个内角之和始终为180°。

• 三角形由它的三条边、三个角和三个顶点定义。

• 三角形的两条边的长度之和大于其第三边的长度。

• 三角形的面积等于其底和高乘积的一半。

• 三角形的周长是三角形三条边的和。

• 全等性质

全等性质指出，如果两个三角形的对应边和角都相等，则这两个三角形全等。

利用坐标计算三角形的面积

坐标几何是利用坐标点研究几何学的方法。如果在坐标平面上给出三角形的三个顶点，则可以确定三角形的面积。

考虑以下三个点：A(1,3)、B(4,1)和C(6,4)。当这三个点在平面上绘出时，它们是非共线的，这意味着它们可以作为三角形的顶点，如下所示：

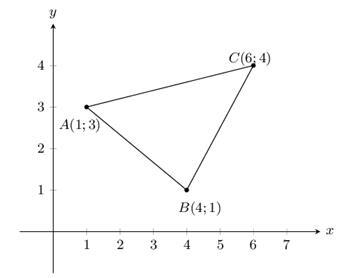
现在我们可以使用坐标几何来计算这个三角形的面积。让我们在下面的部分中了解更多关于它的信息。

在坐标几何中计算三角形面积的方法

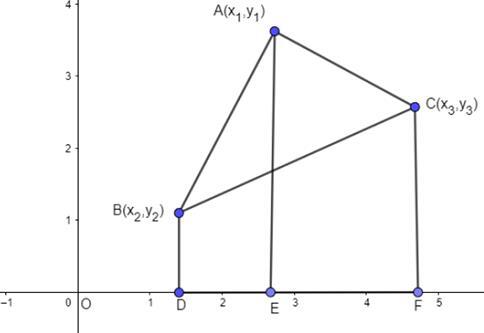
在坐标几何中，我们利用三个顶点的坐标来计算三角形的面积。考虑三角形ABC，其顶点为A (x₁,y₁) B (x₂,y₂)和C (x₃,y₃)。

在此图中，从三角形的顶点到水平轴绘制了垂线AE、CF和BD。形成了三个梯形：BAED、ACFE和BCFD。

三角形的面积可以用这三个梯形的面积来表示。

面积(ΔABC) = 面积(梯形BAED) + 面积(梯形ACFE) - 面积(梯形BCFD)

考虑任何一个梯形，例如BAED。它有两个底，BD和AE，以及一个高DE。BD和AE分别是B和A的y坐标，而DE是A和B的x坐标之差。另外两个梯形的底和高也很容易计算。因此，我们有

面积(ΔABC) = 面积(梯形BAED) + 面积(梯形ACFE) - 面积(梯形BCFD)

$$\mathrm{面积(\Delta ABC) =\frac{1}{2}×[(y_2+y_1)×(x_1-x_2)]+\frac{1}{2}×[(y_1+y_3)×(x_3-x_1)]+\frac{1}{2}×[(y_2+y_3)×(x_3-x_2)]}$$

$$\mathrm{面积(面积(\Delta ABC) =\frac{1}{2}×|x_1 (y_2-y_3)+x_2 (y_3-y_1)+x_3 (y_1-y_2)|}$$

此公式也可以写成行列式形式：

$$\mathrm{面积 = \begin{bmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{bmatrix}}$$

三角形的面积不能为负。如果我们得到一个负结果，我们应该计算面积的数值，而不考虑负号。

利用三角形的面积判断三点共线

• 共线点是指位于同一条直线或同一平面上的点。在欧几里得几何中，位于一条线上彼此靠近或远离的两点或多点被称为共线。

• 如果由这三个点形成的三角形的面积等于零，则这三个点是共线的。

• 在三角形面积公式中，代入给定的三个点的坐标。如果三角形的面积为0，则称给定的点是共线的。

例题

1) 求坐标为A (0,0) B (0,1)和C (1,0)的三角形的面积。

答案：已知坐标为A (0,0) B (0,1)和C (1,0)。

我们知道行列式形式的公式为：

$$\mathrm{面积 = \begin{bmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{bmatrix}}$$

现在代入值：

$$\mathrm{面积 = \begin{bmatrix}0 & 0 & 1 \\0 & 1 & 1 \\1 & 0 & 1\end{bmatrix}}$$

现在沿第一行展开 $\mathrm{面积(\Delta ABC) =\frac{1}{2}× |0+0+1(0-1)|}$

$$\mathrm{\Rightarrow \frac{1}{2}}$$

2) 求给定三角形的面积。

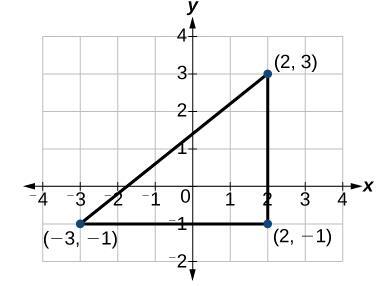
答案：已知坐标为A (-3,-1) B (2,-1)和C (2,3)。

我们知道行列式形式的公式为：

$$\mathrm{面积 = \begin{bmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{bmatrix}}$$

现在代入值：

$$\mathrm{面积 = \begin{bmatrix}-3 & -1 & 1 \\2 & -1 & 1 \\2 & 3 & 1\end{bmatrix}}$$

现在沿第一行展开面积(ΔABC)

$$\mathrm{\Rightarrow \frac{1}{2} |[-3(-1-3)+1(2-2)+1(6+2)]|}$$

$$\mathrm{\Rightarrow 8}$$

3) 求给定三角形的面积。

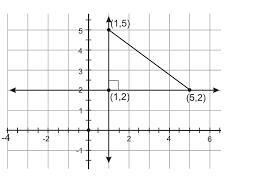
答案：已知坐标为A (1,2) B (5,2)和C (1,5)。

我们知道行列式形式的公式为：

$$\mathrm{面积 = \begin{bmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{bmatrix}}$$

现在代入值：

$$\mathrm{面积 = \begin{bmatrix}1 & 2 & 1 \\5 & 2 & 1 \\1 & 5 & 1\end{bmatrix}}$$

现在沿第一行展开面积(ΔABC)

$$\mathrm{\Rightarrow \frac{1}{2} |[1(2-5)-2(5-1)+1(25-2)]|}$$

$$\mathrm{\Rightarrow 12}$$

结论

在几何学中，三角形是一个有三条边和三个顶点的三边形。三角形的面积是它在二维平面中占据的空间。如果由这三个点形成的三角形的面积等于零，则这三个点是共线的。

常见问题

1. 坐标几何是什么意思？

坐标几何是数学的一个分支，它有助于在二维平面上呈现几何图形并学习这些图形的特性。

2. 什么是三角形？

在几何学中，三角形是具有三条边和三个顶点的多边形。它是二维的，具有三条直边。

3. 三角形的面积是多少？

三角形的面积是它在二维平面中占据的空间。

4. 求三角形面积的公式是什么？

求三角形面积的公式：

$$\mathrm{面积 = \begin{bmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{bmatrix}}$$

5. 如何判断给定的三个点是否共线？

如果由这三个点形成的三角形的面积等于零，则这三个点是共线的。