数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法学研究
已知：(i) $(82)^2 – (18)^2$ (ii) $(467)^2 – (33)^2$ (iii) $(79)^2 – (69)^2$ (iv) $197 \times 203$ (v) $113 \times 87$ (vi) $95 \times 105$ (vii) $1.8 \times 2.2$ (viii) $9.8 \times 10.2$ 要求：我们必须使用公式 $(a – b) (a + b) = a^2 – b^2$ 简化给定的表达式。解答：这里，我们必须使用公式 $(a – b) (a + b) = a^2 – b^2$ 简化给定的表达式。给定的表达式可以通过将项写成两个合适数字的和或差来写成两个平方差的形式。(i) 给定的表达式是 $(82)^2 – ... 阅读更多
已知：(i) $\frac{((58)^2 – (42)^2)}{16}$ (ii) $178 \times 178 – 22 \times 22$ (iii) $\frac{(198 \times 198 – 102 \times 102)}{96}$ (iv) $1.73 \times 1.73 – 0.27 \times 0.27$ (v) $\frac{(8.63 \times 8.63 – 1.37 \times 1.37)}{0.726}$ 要求：我们必须使用合适的恒等式简化给定的表达式。解答：这里，我们必须简化给定的表达式。给定的表达式（表达式中的分子）是两个平方数之差的形式。我们可以使用恒等式 $a^2-b^2=(a+b) \times (a-b)$ 简化给定的表达式。(i) 给定的表达式是 $\frac{((58)^2 – (42)^2)}{16}$ 这里，$a=58$ 且 $b=42$ 因此，$\frac{((58)^2 – (42)^2)}{16}=\frac{(58+42) \times (58-42)}{16}$$\frac{((58)^2 – (42)^2)}{16}=\frac{100\times16}{16}$$\frac{((58)^2 – (42)^2)}{16}=100$ 因此，... 阅读更多
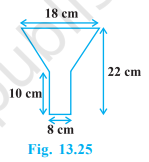
已知：一个用锡片制成的油漏斗由一个 10 厘米长的圆柱形部分和一个圆锥台组成。总高度为 22 厘米，圆柱形部分的直径为 8 厘米，漏斗顶部的直径为 18 厘米。要求：我们必须找到制作漏斗所需的锡片面积。解答：圆锥台顶端圆形末端的直径 = 18 厘米这意味着，圆锥台顶端圆形末端的半径 (r₁) = 9 厘米底部圆形末端的半径…… 阅读更多
引言 遗传密码是一套规则，它决定了核苷酸三联体（密码子）与其指定的氨基酸之间的对应关系。在遗传学的语言中，终止密码子或终止密码子是信使RNA（mRNA）中的一种核苷酸三联体，它表示蛋白质编码序列的结束。终止密码子对于蛋白质合成的正确终止至关重要，并在基因表达的调控中起着至关重要的作用。什么是终止密码子？终止密码子，也称为终止密码子，是信使RNA（mRNA）中的一组三个核苷酸序列，它表示…… 阅读更多
引言和历史 膜是每个活细胞的重要组成部分，它将细胞与其外部环境隔开，并为分子的自由移动提供屏障。细胞膜的发现归功于 17 世纪罗伯特·胡克和安东尼·范·列文虎克的实验，他们首先在显微镜下观察到细胞和细菌。在 19 世纪，研究人员发现细胞被一层薄薄的物质包围着，后来被称为细胞膜。细胞膜的结构和组成的概念开始成形…… 阅读更多
引言 蛋白质合成是发生在所有活生物体中的一个基本过程。它涉及从 DNA 中编码的遗传信息产生蛋白质。蛋白质合成的过程涉及多个步骤，其中一个步骤是翻译的起始。翻译的起始受起始密码子（也称为 AUG 密码子）的调控。起始密码子/AUG 密码子的定义 起始密码子，也称为起始密码子或 AUG 密码子，是 mRNA 的三个核苷酸序列，它向核糖体发出开始蛋白质合成的信号。它始终是 mRNA 序列中的第一个密码子…… 阅读更多
引言 转录是发生在所有活生物体中的一个过程，其中以DNA形式存在的遗传信息被转换成功能性的RNA分子。RNA是核苷酸的聚合物，在蛋白质合成中起着关键作用。转录是基因表达的第一步，是一个涉及一系列阶段的复杂过程。在本教程中，我们将详细探讨转录的不同阶段。起始 转录的起始阶段始于RNA聚合酶识别DNA的特定区域（称为启动子），……阅读更多
驾驶需要集中注意力、专心和耐心。无论您是经验丰富的司机还是最近才学会驾驶，只要您的手握着方向盘，就需要时刻注意某些事项。自动挡汽车占据了超过60%的市场份额，在人们中变得越来越普遍。如今，大多数人都很乐意驾驶自动挡汽车，但并非每个人都知道如何操作手动挡汽车。本文旨在帮助人们学习驾驶自动挡和手动挡车辆。第一部分：做好准备 在学习驾驶之前，您应该做好心理准备……阅读更多
引言 让我们尝试了解使用LINQ估算文件大小的C#程序。我们将了解LINQ（语言集成查询）及其方法和类，以及如何利用它们获得所需的输出。语言集成查询，即LINQ，用于在C#语言中生成查询。以前，我们必须使用其他关系语言，如SQL和XML。它为C#语言或任何其他.NET语言提供了更强大的功能。在LINQ中用于查询数据库的语法与查询数据……阅读更多