数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学
题目：我们必须回答给出的问题。解答：(a) Munnu 的年龄是 \( x \) 岁。$(x - 2)$ 表示比 Munnu 小 2 岁的年龄。$(x + 4)$ 表示比 Munnu 大 4 岁的年龄。$(3x + 7)$ 表示比 Munnu 年长的人的年龄，他的年龄是 Munnu 年龄的三倍加 7 岁。(b) Sara 今天的年龄是 \( y \) 岁。$(y + 7)$ 表示比 Sara 大 7 岁的人的年龄。$(y - 3)$ 表示… 阅读更多
题目：我们必须找出给定表达式中哪些是方程（含变量）。解答：方程是变量和/或数字组成的两个表达式之间的等式。(a) \( 17=x+7 \) 是一个含变量 $x$ 的方程。(b) \( (t-7)>5 \) 是一个不等式，而不是方程。(c) \( \frac{4}{2}=2 \) 是一个数值方程。(d) \( (7 \times 3)-19=8 \) 是一个数值方程。(e) \( 5 \times 4-8=2 x \) 是一个含变量 $x$ 的方程。(f) \( x-2=0 \) 是一个含变量 $x$ 的方程。(g) \( 2 m
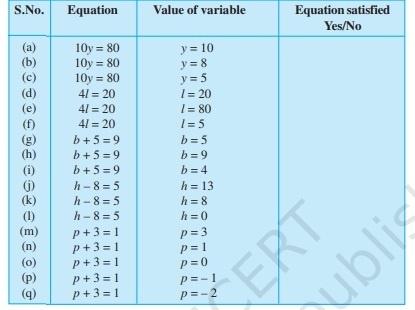
"\题目：我们必须完成给定表格第三列的条目。解答：(a) $10y = 80$如果 $y = 10$ 那么 $10y=10(10)=100$ $y=10$ 不是方程 $10y = 80$ 的解，因此方程不成立。(b) $10y = 80$如果 $y = 8$ 那么 $10y=10(8)=80$ $y=8$ 是方程 $10y = 80$ 的解，因此方程成立。(c) $10y = 50$如果 $y = 5$ 那么 $10y=10(5)=50$ $y=5$ 不是方程 $10y = 80$ 的解，因此… 阅读更多
题目：我们必须找到以下比率：(a) 矩形内三角形数量与圆形数量的比率。(b) 矩形内正方形数量与所有图形数量的比率。(c) 矩形内圆形数量与所有图形数量的比率。解答：从图中我们可以看出，有 3 个三角形，2 个正方形和 2 个圆形。因此，图形总数 = 7 (a) 矩形内三角形数量与圆形数量的比率 = 3:2。(b) 矩形内正方形数量与所有图形数量的比率 = 2:7。(c) 矩形内圆形数量与所有图形数量的… 阅读更多
题目：我们必须用变量 \( a, b \) 和 \( c \) 以一般方式表达给定的性质。解答：$(14+27)+13=41+13=54$ $14+(27+13)=14+40=54$ 令 $a=14, b=27, c=13$ 这意味着，$(a+b)+c=a+(b+c)$ 因此，对于任何三个整数 $a, b$ 和 $c$，$(a + b) + c = a + (b + c)$
"
已知：圆的直径是一条连接圆上两点并通过圆心的线。在给定图中，\( \mathrm{AB} \) 是圆的直径；\( \mathrm{C} \) 是其圆心。题目：我们必须用其半径 \( (r) \) 表示圆的直径 \( (d) \)。解答：\( \mathrm{AB} \) 是圆的直径从图中，$AB=AC+BC$$=r+r$$=2r$$d=2r$ 用其半径 \( (r) \) 表示圆的直径 \( (d) \) 为 $d=2r$。
题目：我们必须用三个数字 5、7 和 8 构造尽可能多的表达式（无变量）。解答：由 5、7 和 8 组成的部分表达式如下所示：$5+(8-7)$ $5-(8-7)$ $5-(8+7)$ $(5 \times 8)+7$ $(5 \times8) - 7)$ $5 \times (8 + 7)$ $(7 + 5) \times 8$ $(8 – 5) \times 7$ $(8 + 5) \times 7$ $(7 – 5) \times 8$
题目：我们必须找到只有数字的表达式。解答：变量：变量用可以取任何实数值的符号表示。变量的值不是固定的。字母$x, y$和$z$通常用于表示变量。因此，(a) $y+3$ 是一个包含变量$y$的表达式。(b) $(7\times 20)-8z$ 是一个包含变量$z$的表达式。(c) $5(21-7)+7\times2$ 是一个只有数字的表达式。(d) 5 是一个只有数字的表达式。(e) $3x$ 是一个包含变量$x$的表达式。(f) $5-5n$ 是一个包含变量$n$的表达式。(g) $(7\times 20)-(5\times 10)-45+p$ 是一个包含变量$p$的表达式。因此，$5(21-7)+7\times2$ 和 5 是只有数字的表达式。阅读更多
题目：我们必须确定构成给定表达式的运算（加法、减法、除法、乘法），并说明这些表达式的构成方式。解答：(a) $z + 1$ --> 1 加到 $z$ 上 使用了加法运算 $z - 1$ --> 从 $z$ 中减去 1 使用了减法运算 $y + 17$ --> 17 加到 $y$ 上 使用了加法运算 $y - 17$ --> 从 $y$ 中减去 17 使用了减法运算 (b) $17y$ --> $y$ 乘以 17 使用了乘法运算 $\frac{y}{17}$ --> $y$ 除以 17 使用了除法运算 $5z$ --> $z$ 乘以 5 ... 阅读更多
题目：我们必须将给定的语句写成表达式。解答：(a) 将 7 加到 $p$ 上是 $p+7$。(b) 从 $p$ 中减去 7 是 $p-7$。(c) $p$ 乘以 7 是 $7p$ (d) $p$ 除以 7 是 $\frac{p}{7}$ (e) 从 $-m$ 中减去 7 是 $(-m-7)$ (f) $-p$ 乘以 5 是 $(-5p)$ (g) $-p$ 除以 5 是 $(\frac{-p}{5})$ (h) $p$ 乘以 $-5$ 是 $(-5p)$