数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法学
待办事项：我们需要验证等腰三角形的垂线和中线是否可以相同。解决方案：按照以下步骤操作：画一个△PQR，其中PQ = PR。让我们画一条线段PS，垂直于QR。PS是三角形的垂线。通过测量可以观察到QS和SR的长度也相同。因此，S是QR的中点。因此，PS也是该三角形的中线。在这里，我们观察到等腰三角形PQR中的垂线PS也是其中线。
待办事项：我们需要为以下内容绘制草图：(a) 在△ABC中，BE是一条中线。(b) 在△PQR中，PQ和PR是三角形的垂线。(c) 在△XYZ中，YL是三角形外的一条垂线。解决方案：(a)三角形的中线是从一个顶点到对面边中点的线段。在△ABC中，BE是中线。(b)三角形的垂线是从三角形的顶点到对面边所作的垂直线。△PQR是一个直角三角形，其中PQ和QR是垂线。(c)△XYZ是一个钝角…阅读更多
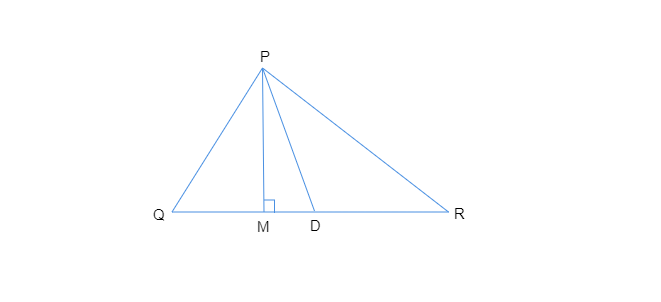
已知：在△PQR中，D是QR的中点。待办事项：我们需要在△PQR中命名PM、PD，并找出QM是否等于MR。解决方案：三角形的垂线是从三角形的顶点到对面边所作的垂直线。在给定图形中，PM垂直于QR。因此，PM是垂线。三角形的中线是从一个顶点到对面边中点的线段。PD将QR分成相等的两部分，因为D是QR的中点。因此，PD是中线。在△PQR中，D是…阅读更多
"
待办事项：我们需要找出通过放大镜观察时角度是否变大。解决方案：即使我们通过放大镜观察，角度的度数仍然是30°。因此，通过放大镜观察不会改变角度的度数。
"
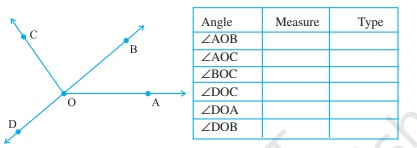
待办事项：我们需要测量并分类每个角度。解决方案：使用量角器，∠AOB的度数为40°，它是锐角。∠AOC的度数为125°，它是钝角。∠BOC的度数为85°，它是锐角。∠DOC的度数为95°，它是钝角。∠DOA的度数为140°，它是钝角。∠DOB的度数为180°，它是平角。
"
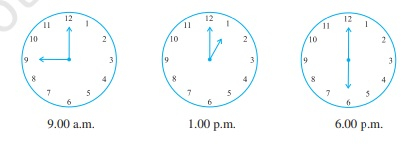
待办事项：我们需要找出每个图中钟表指针之间的角度。解决方案：圆的完整角度为360°。这意味着，任何两个相邻数字之间的角度=360°/12=30°。因此，上午9:00时钟表指针之间的角度=3×30°=90°。下午1:00时钟表指针之间的角度=1×30°=30°。下午6:00时钟表指针之间的角度=6×30°=180°。
"
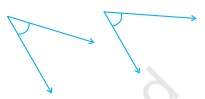
待办事项：我们需要找出哪个角度更大。解决方案：第一个角度的估计值：等于直角的一半。使用量角器测量角度，第一个角度等于45°。第二个角度的估计值：等于直角的三分之二。使用量角器测量角度，第二个角度等于55°。因此，第二个角度更大。
待办事项：我们需要填空。解决方案：(a) 一个角度的度数小于直角是锐角。(b) 一个角度的度数大于直角是钝角。(c) 一个角度的度数等于两个直角的度数之和是平角。(d) 当两个角度的度数之和等于直角时，则每个角度都是锐角。(e) 当两个角度的度数之和等于平角，且其中一个角度是锐角时，则另一个…阅读更多
"
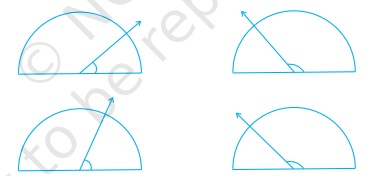
待办事项：我们需要找出每个图中所示的角度。解决方案：第一个角度的估计值：等于直角的一半。使用量角器测量角度，第一个角度等于40°。第二个角度的估计值：等于平角的四分之三。使用量角器测量角度，第二个角度等于130°。第三个角度的估计值：等于直角的三分之二。使用量角器测量角度，第三个角度等于65°。第四个角度的估计值：等于…阅读更多
"
待办事项：我们需要找出哪个角度更大。解决方案：∠A的估计值：等于直角的一半。使用量角器测量角度，A = 40°。∠B的估计值：等于直角的三分之二。使用量角器测量角度，B = 68°。因此，B = 68°更大。