解题:我们需要判断在每种情况下 $l$ 是否平行于 $m$。解:我们知道,同旁内角和为 $180^o$。(i) 这里,直线 $n$ 同旁内角和为 $126^{\circ}+44^{\circ}$$=170^{\circ}$$≠180^{\circ}$因此,$l$ 不平行于 $m$。(ii) 令与 $75^{\circ}$ 互为对顶角的角为 $x$。$x=75^{\circ}$ [对顶角相等]直线 $n$ 同旁内角和为 $x+75^{\circ}$$=75^{\circ}+75^{\circ}$$=150^{\circ}$$≠180^{\circ}$因此,$l$ 不平行于 $m$。(iii) 令与 $57^{\circ}$ 互为对顶角的角为 $y$因此,$y=57^{\circ}$ ... 阅读更多
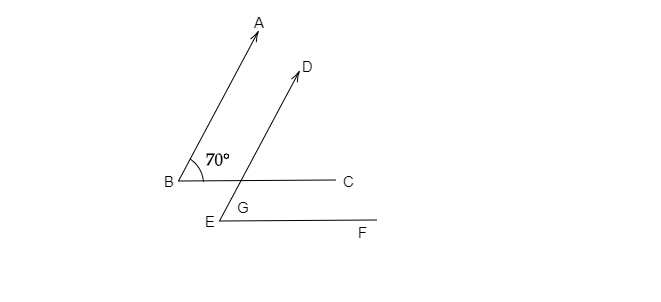
已知:在如图所示中,两个角的两条边互相平行。$\angle ABC = 70^{\circ}$。解题:我们需要求(i) $\angle DGC$(ii) $\angle DEF$解:$AB \| DE$ [已知]$BC \| EF$ [已知]$\angle ABC=70^{\circ}$$\angle ABC$ 和 $\angle DEF$ 是一对同位角。这意味着,$\angle DEF=\angle ABC$(i) $AB \| DE$这意味着,$AB \| DG$$\angle DGC=\angle ABC=70^{\circ}$ [同位角相等](ii) $BC \| EF$这意味着,$GC \| EF$$\angle DEF=\angle DGC=70^{\circ}$ [同位角相等]
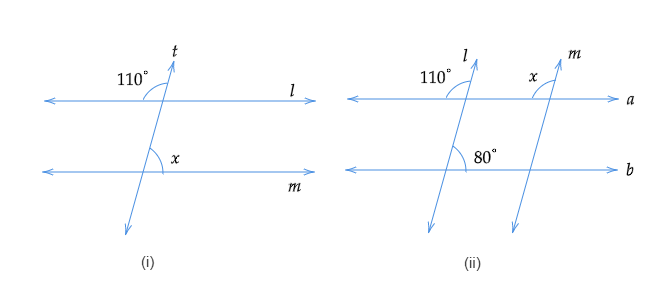
解题:如果 $l \| m$,我们需要在每幅图中求 $x$ 的值。解:(i) 令与 $110^{\circ}$ 互为对顶角的角为 $y$。因此,$y=110^{\circ}$ [对顶角相等]$\angle x+\angle y=180^{\circ}$ [同旁内角和为 $180^o$]$\angle x+110^{\circ}=180^{\circ}$因此,$\angle x=180^{\circ}-110^{\circ}$$=70^{\circ}$因此 $x=70^{\circ}$(ii) $\angle x=100^{\circ}$ [同位角相等]
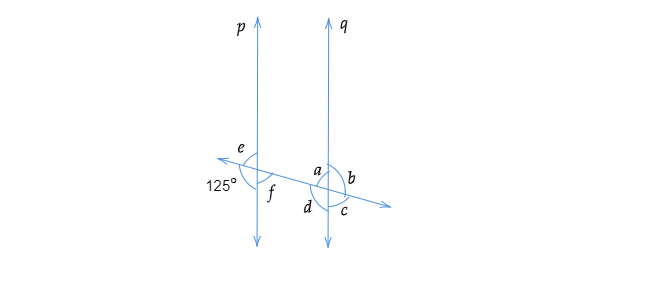
已知: $p \| q$。解题:我们需要求未知角。解:$\angle e$ 和 $125^o$ 构成一个线性对。因此,$\angle e+125^o=180^o$$\angle e=180^{\circ}-125^{\circ}$$=55^{\circ}$$\angle e=\angle f$ [对顶角相等]因此, $\angle f=55^{\circ}$$\angle a=\angle f=55^{\circ}$ [内错角相等]$\angle c=\angle a=55^{\circ}$ [对顶角相等]$\angle d=125^{\circ}$ [同位角相等]$\angle b=\angle d=125^{\circ}$ [对顶角相等]因此, $\angle a=55^{\circ},\ \angle b=125^{\circ},\ \angle c=55^{\circ},\ \angle d=125^{\circ},\ \angle e=55^{\circ},\ \angle f=55^{\circ}$
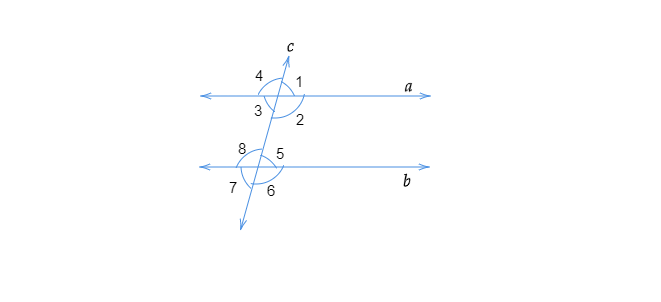
解题:我们需要确定(i) 同位角。(ii) 内错角。(iii) 同旁内角。(iv) 对顶角。解:(i) 同位角是 $\angle 1$ 和 $\angle 5, \ \angle 2$ 和 $\angle 6, \ \angle 4$ 和 $\angle 8, \ \angle 3$ 和 $\angle 7$(ii) 内错角是 $\angle 2$ 和 $\angle 8$; $\angle3$ 和 $\angle 5$(iii) 同旁内角是 $\angle 2$ 和 $\angle 5, \ \angle 3$ 和 $\angle ... 阅读更多
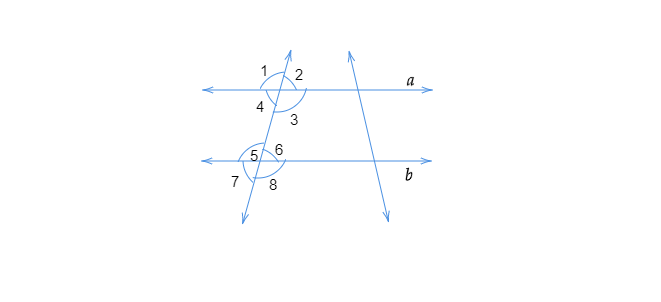
解题:我们需要说明在每个给定陈述中使用了什么性质。解:(i) 给定 $a \| b$我们知道,如果两条直线平行,则一对同位角相等。因此,$\angle1=\angle5$在给定陈述中使用了同位角性质。(ii) 给定 $\angle 4=\angle 6$如果一对内错角相等,则两条直线平行因此,$a \| b$在给定陈述中使用了同位角性质。(iii) 给定 $\angle4+\angle5=180^{\circ}$如果内角和为 $180^{\circ}$,则两条直线平行因此,$a \| b$同旁内角互补。阅读更多
解题:我们需要填写给定的空格。解:(i) 如果两个角互余,则它们的度数之和为 $90^{\circ}$。(ii) 如果两个角互补,则它们的度数之和为 $180^{\circ}$。(iii) 构成线性对的两个角是 互补的。(iv) 如果两个邻角互补,则它们构成一个 线性对。(v) 如果两条直线相交于一点,则对顶角总是 相等。(vi) 如果两条直线相交于一点,且一对对顶角是锐角,则另一对对顶角是 钝角。阅读更多
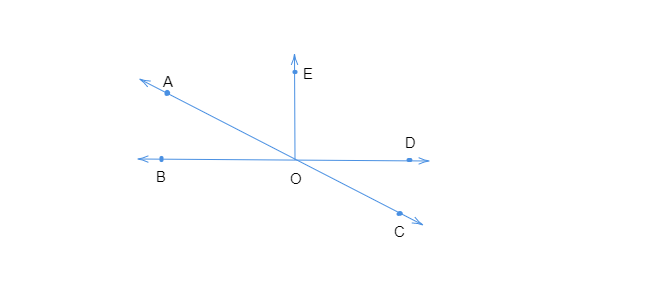
解题:我们需要命名 (i) 钝角对顶角(ii) 邻补角(iii) 相等的补角(iv) 不相等的补角(v) 不构成线性对的邻角解:(i) 大于 $90^o$ 且构成一对对顶角的角称为 钝角对顶角。因此,$\angle BOC$ 和 $\angle AOD$ 是钝角对顶角。(ii) 有一个公共顶点、一条公共边,且非公共边位于公共边的两侧,且和为 $90^o$ 的角称为 邻补角。因此,$\angle AOB$ 和 $\angle AOE$ 是邻补角。(iii) 相等的补角称为 相等的补角 ... 阅读更多
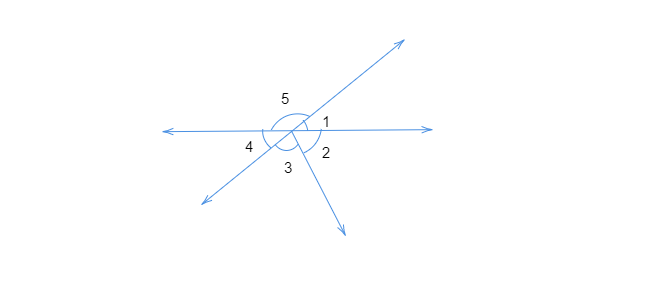
解题:我们需要指出哪几对角是:(i) 对顶角。(ii) 线性对。解:对顶角是由两条直线相交形成的角。线性对是指两个邻角之和为 $180^o$。因此,(i) 对顶角是 $\angle 1$ 和 $\angle 4;\ \angle 5$ 和 $(\angle 2+\angle 3)$(ii) 线性对是 $\angle 1$ 和 $\angle 5$, $\angle 5$ 和 $\angle 4$。
待解决问题:如果两个角都是以下情况,我们是否需要判断这两个角是否互为补角?(i)锐角(ii)钝角(iii)直角解:(i)我们知道,锐角$< 90^{\circ}$因此,锐角$+$锐角$< 90^{\circ}+90^{\circ}$这意味着,锐角$+$锐角$< 180^{\circ}$因此,两个锐角不能互为补角。(ii)我们知道,钝角$> 90^{\circ}$这意味着,钝角$+$钝角$> 90^{\circ}+90^{\circ}$钝角$+$钝角$>180^{\circ}$因此,两个钝角不能互为补角。(iii)我们知道,直角$=90^{\circ}$这意味着,直角$+$直角$=90^{\circ}+90^{\circ}$$=180^{\circ}$因此,两个直角构成一对互为补角。阅读更多

 数据结构
数据结构 网络
网络 关系型数据库管理系统
关系型数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP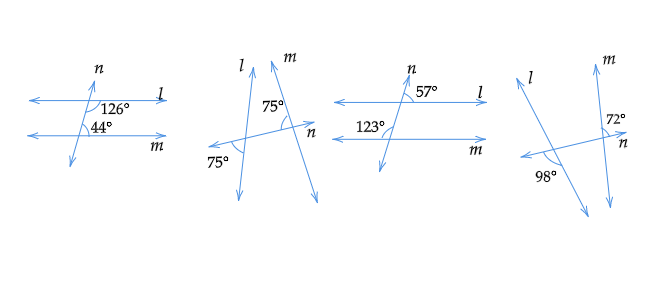 "
"

 "
"
 "
"
 "
"