数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
已知：一根长 15 米的梯子，放在墙边，梯子的顶端到达离地面 12 米高处的窗户，梯子底部到墙的距离为 a。求：梯子底部到墙的距离。解：设梯子为 AC，窗户为 A，则 AC²=AB²+BC² ⇒ (15)²=(a)²+(12)² ⇒ 225-144=a² ⇒ 81=a² ⇒ √81=a ⇒ a=9
已知：ABCD 是一个四边形。求：是否 AB + BC + CD + DA < 2 (AC + BD)？解：三角形中任意两边的长度之和大于第三边的长度。在△AOB 中，AB+ob> 在△BOC 中，BC+oc> 在△COD 中，CD+od> 在△AOD 中，DA+od> 将 (i)、(ii)、(iii) 和 (iv) 相加 AB+BC+CD+DA AB+BC+CD+DAAB+BC+CD+DAAB+BC+CD+DA 证毕！
已知：ABCD 是一个四边形。求：是否 AB + BC + CD + DA > AC + BD？解：三角形中任意两边的长度之和大于第三边的长度，因此在△ABC 中，AB+BC>AC .......(i)△ADC 中，AD+DC>AC， .......(ii)△DCB 中，DC+CB>DB， .......(iii)△ADB 中，AD+AB>DB， .......(iv)将方程 (i)、(ii)、(iii) 和 (iv) 相加 AB+BC+AD+DC+DC+CB+AD+AB>AC+AC+DB+DB (AB+AB)+(BC+BC)+(AD+AD)+(DC+DC)>2AC+2DB 2AB+2BC+2AD+2DC>2AC+2DB 2(AB+BC+AD+DC)>2(AC+DB) AB+BC+AD+DC>AC+DB 阅读更多
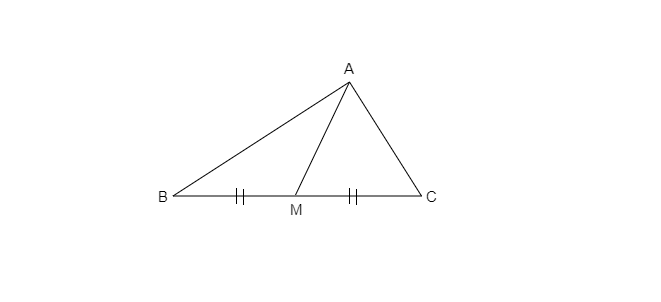
已知：AM 是三角形 ABC 的中线。求：是否 AB + BC + CA > 2 AM？解：让我们考虑△ABM 和△AMC众所周知，三角形中任意两边的长度之和大于第三边的长度。在△ABM 中：AB+BM>AM ......(i)在△AMC 中：AC+MC>AM ......(ii)让我们将 (i) 和 (ii) 相加 AB+BM+AC+MC>AM+AM ⇒ AB+AC+(BM+MC)>2AM ⇒ AB+AC+BC>2AM 证毕！
已知：边长：（i）. 2 厘米、3 厘米、5 厘米（ii）. 3 厘米、6 厘米、7 厘米（iii）. 6 厘米、3 厘米、2 厘米求：检查是否可以有一个三角形，其边长为给定值。解：在一个三角形中，其两边的长度之和总是大于第三边的长度。现在我们将使用此标准检查给定的边长：（i）. 2+3>5，否2+5>3，是3+5>2，是该三角形不可能存在。（ii）. 3+6>7，是6+7>3，是3+7>6，是该三角形可能存在。（iii）. 6+3>2，是6+2>3，是2+3>6，否该三角形不可能存在。
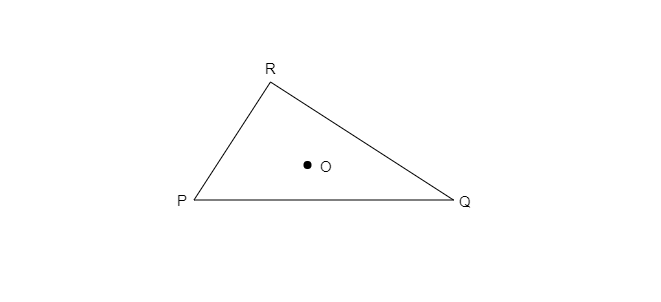
已知：一个三角形 PQR。求：在三角形 PQR 的内部取任意一点 O。并找出是否：（i）. OP + OQ > PQ？(ii). OQ + OR > QR？(iii). OR + OP > RP？解：(i). 连接 OR、OQ 和 OP在△OPQ 中，OP+OR>PQ 是的，POQ 形成了一个三角形。(ii) 在△ORQ 中OQ+OR>QR 是的，ORQ 形成了一个三角形。(iii) 在△ORP 中OR+OP>PR 是的，ORP 形成了一个三角形。
"
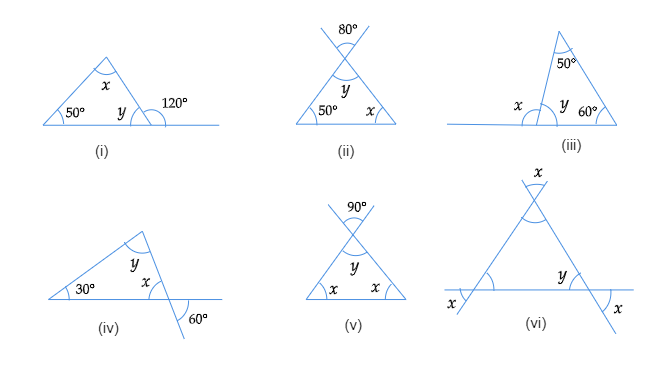
已知：上图中带有未知角 x 和 y 的三角形。求：在每种情况下，求未知角 x 和 y 的值。解：为方便起见，我们将图中给出的所有三角形命名为△ABC。(i). ∠y+∠ACD=180° [线性对]⇒ ∠y + 120°=180°⇒ ∠y=60°根据角和性质在三角形 ABC 中∠A+∠B+∠C=180° [∠A=x，∠C=y]⇒ x+50°+60°=180°⇒ x=180°-110°⇒ x=70°(ii). ∠EAD=∠y [对顶角相等]80°=∠y根据角和性质在三角形 ABC 中∠A+∠B+∠C=180°⇒ 80°+ 50° +x=180°⇒ ... 阅读更多
"
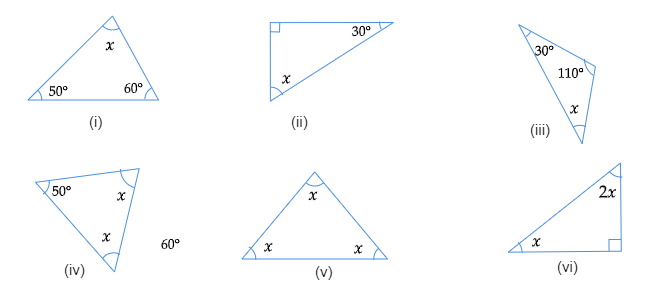
已知：上图中带有未知角 x 的三角形。求：在每种情况下，求未知角 x 的值。解：(i). 根据三角形的角和性质x+50°+60°=180°⇒ x=180°-110°⇒ x=70°(ii). 根据三角形的角和性质90°+30°+x=180°⇒ x=180°-120°⇒ x=60°(iii). 根据三角形的角和性质30°+ 110°+x=180°⇒ x=180°-140°⇒ x=40°(iv). 根据三角形的角和性质50°+x+x=180°⇒ 50°+2x=80°⇒ x=130/2 ⇒ x=65°(v). 根据三角形的角和性质x+x+x=180°⇒ 3x=180°⇒ x=180/3 ⇒ x=60°(vi). 根据三角形的角和性质2x+90°+x=180°⇒ 3x=180°-90°⇒ x=90/3x ⇒ x=30°另一个角 = 2x=2×30=60°阅读更多
"
求解：我们需要在每种情况下找到未知内角 x 的值。解：为方便起见，我们将图中给出的所有三角形命名为△ABC。我们知道，三角形的外角等于其内对角的和。因此，(i) ∠A+x=∠ACD ⇒ 50°+ x=115°⇒ x=115°-50°⇒ x=65°(ii) ∠A+x=∠CBD ⇒ 70°+ x=100°⇒ x=100°- 70°⇒ x=30°(iii) ∠C+x=∠BAD ⇒ 90°+x=125°⇒ x=125°- 90°⇒ x=35°(iv) ∠A+x=∠ABD ⇒ 60°+ x=120°⇒ x=120°-60°⇒ x = 60°(v) ∠B+x=∠CAD ⇒ 30°+ x=80°⇒ x=80°- 30°⇒ x=50°(vi) ∠B+x=∠BCD ⇒ 35°+ x=75°⇒ x=75°-35°⇒ x=40° 阅读更多
"
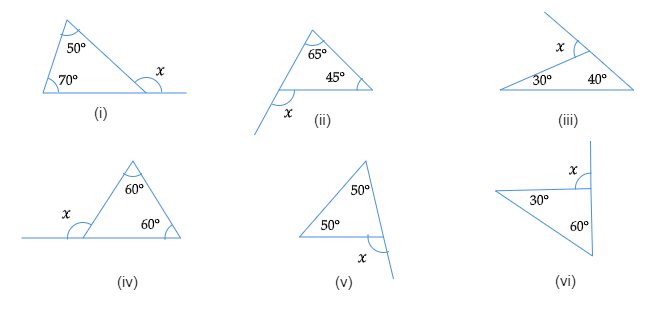
待解决问题：在每种情况下，我们都需要找到未知的外角x。解答：为了方便起见，我们将图中给出的所有三角形命名为△ABC。我们知道，三角形的外角等于其两个内对角的和。因此，(i) ∠BAC + ∠ABC = x ⇒ 70° + 50° = x ⇒ x = 120°(ii) ∠BAC + ∠ACB = x ⇒ 65° + 45° = x ⇒ x = 110°(iii) ∠CAB + ∠ABC = x ⇒ 30° + 40° = x ⇒ x = 70°(iv) ∠BCA + ∠BAC = x ⇒ 60° + 60° = x ⇒ x = 120°(v) ∠BAC + ∠ABC = x ⇒ 50° + 50° = x ⇒ x = 100°(vi) ∠BAC + ∠ABC = x ⇒ 30° + 60° = x ⇒ x = 90° 阅读更多