$(i).\ OP + OQ > PQ?$
$(ii).\ OQ + OR > QR?$
$(iii).\ OR + OP > RP?$

在三角形PQR内部取任意一点O。

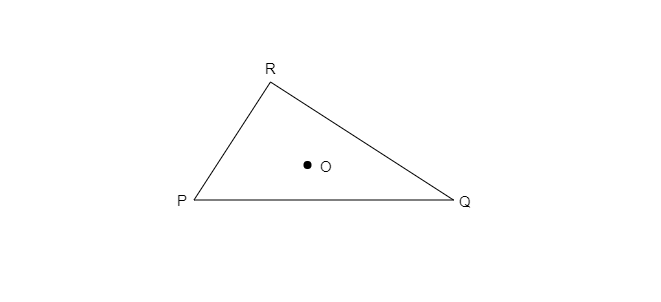
$(i).\ OP + OQ > PQ?$
$(ii).\ OQ + OR > QR?$
$(iii).\ OR + OP > RP?$

已知：三角形PQR。

求证：在三角形PQR内部取任意一点O，并确定是否

$(i).\ OP + OQ > PQ?$

$(ii).\ OQ + OR > QR?$

$(iii).\ OR + OP > RP?$


解答

$(i)$ 连接OR，OQ和OP

在$\triangle OPQ$中，

$OP+OQ>PQ$

是的，POQ构成一个三角形。

$(ii)$ 在$\triangle ORQ$中

$OQ+OR>QR$

是的，ORQ构成一个三角形。

$(iii)$ 在$\triangle ORP$中

$OR+OP>PR$

是的，ORP构成一个三角形。

更新于：2022年10月10日

浏览量：71

开启你的职业生涯

完成课程获得认证

开始学习
广告