在给定的图形中，$PR>PQ$，且PS平分$\angle QPR$。证明$\angle PSR > \angle PSQ$。

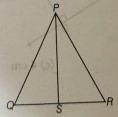
已知

$PR>PQ$，且PS平分$\angle QPR$。

要求

我们必须证明$\angle PSR > \angle PSQ$。

解答

我们知道：

大边对大角。

这意味着：

$\angle PQR > \angle PRQ$

$\angle QPS = \angle RPS$ (PS平分$\angle QPR$)

设$\angle QPS = \angle RPS = x$

在$\triangle PQS$中：

$\angle PSR = \angle PQR + x$......(i) (外角性质)

在$\triangle PSR$中：

$\angle PSQ = \angle PRQ + x$......(ii) (外角性质)

$\angle PQR > \angle PRQ$ (已知)

两边同时加x：

$\angle PQR + x > \angle PRQ + x$

$\angle PSR > \angle PSQ$

证毕。

更新于：2022年10月10日

64次浏览

开启你的职业生涯

完成课程获得认证

开始学习
广告