如图所示，$PQ \parallel AB$ 且 $PR \parallel BC$。如果 $\angle QPR = 102^o$，求 $\angle ABC$ 的度数。请说明理由。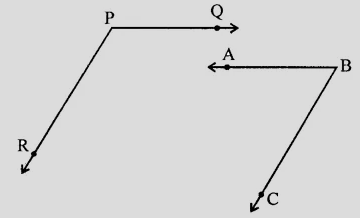

已知

$PQ \parallel AB$ 且 $PR \parallel BC$。

$\angle QPR = 102^o$。

要求

我们必须确定 $\angle ABC$。

解答

延长 $BA$ 交 $PR$ 于 $D$ 点。

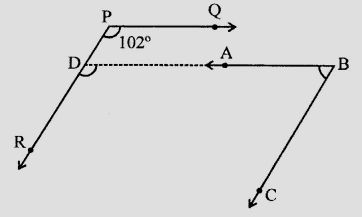
$PQ \parallel AB$

这意味着：

$PQ \parallel DB$

因此：

$\angle QPR = \angle ADR$ (同位角)

$\angle ADR = \angle BDR = 102^o$

$\angle BDR + \angle DBC = 180^o$ (同旁内角和)

$102^o + \angle DBC = 180^o$

$\angle DBC = 180^o - 102^o$

$\angle DBC = 78^o$

这意味着：

$\angle ABC = 78^o$。

因此，$\angle ABC = 78^o$。

Tutorialspoint

更新于：2022年10月10日

浏览量：59

开启您的职业生涯

完成课程获得认证

开始学习