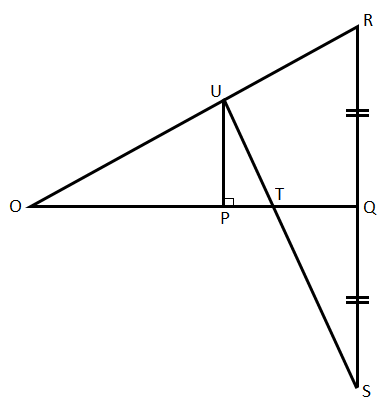
在给定图形中，OQ 是 RS 的垂直平分线，UP 垂直于 OQ。证明 $\frac{1}{OP} \ +\ \frac{1}{OQ} \ =\ \frac{2}{OT}$。
"\n

已知：OQ 是 RS 的垂直平分线，UP 垂直于 OQ。

证明：我们需要证明 $\frac{1}{OP} \ +\ \frac{1}{OQ} \ =\ \frac{2}{OT}$。

解答

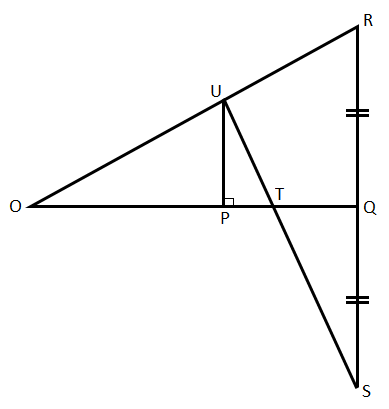
在 ∆POU 和 ∆QOR 中

• ∠O = ∠O (公共角)
• ∠P = ∠Q (均为 90^o)

因此，∆POU ~ ∆QOR（根据角角相似准则）。

在两个相似三角形中，对应边成比例。因此，

$\frac{OP}{OQ} \ =\ \frac{PU}{QR}$ ....(i)

此外，

在 ∆UPT 和 ∆SQT 中

• ∠UTP = ∠STQ (对顶角)
• ∠P = ∠Q (均为 90^o)
  

因此，∆UPT ~ ∆SQT（根据角角相似准则）。

在两个相似三角形中，对应边成比例。因此，

$\frac{PU}{QS} \ =\ \frac{PT}{QT}$

但 QS = QR，因为 Q 是 RS 的中点。所以，

$\frac{PU}{QR} \ =\ \frac{PT}{QT}$ ....(ii)

现在，由 (i) 和 (ii)

$\frac{PT}{QT}\ =\ \frac{OP}{OQ}$

$\frac{OT\ -\ OP}{OQ\ -\ OT}\ =\ \frac{OP}{OQ}$

$( OT\ -\ OP) OQ\ =\ ( OQ\ -\ OT) OP$

$OT\times OQ\ -\ OP\times OQ\ =\ OQ\times OP\ -\ OT\times OP$

$OT\times OQ\ +\ OT\times OP\ =\ OP\times OQ\ +\ OQ\times OP$

$OT( OQ\ +\ OP) \ =\ 2( OQ\ \times \ OP)$

$\frac{OQ\ +\ OP}{OQ\ \times \ OP} \ =\ \frac{2}{OT}$

$\frac{OQ}{OQ\ \times \ OP} \ +\ \frac{OP}{OQ\ \times \ OP} \ =\ \frac{2}{OT}$

$\mathbf{\frac{1}{OP} \ +\ \frac{1}{OQ} \ =\ \frac{2}{OT}}$

所以，证明了 $\frac{1}{OP} \ +\ \frac{1}{OQ} \ =\ \frac{2}{OT}$。

教程点

更新于： 2022-10-10

130 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习